前馈神经网络
前馈神经网络,又称作深度前馈网络、多层感知机,信息流经过中间的函数计算, 最终达到输出,被称为“前向”。模型的输出与模型本身没有反馈连接。
前馈神经网络中的隐含层需要使用非线性激活,如果不使用非线性激活函数,那么每一层都是线性的,导致多层的线性组合仍然是线性的,最终的输出也是线性拟合,无法泛化非线性的问题。
实验要求
- 使用torch.nn在Fashion-MNIST数据集完成前馈神经网络,绘制训练集和测试集的loss曲线(使用Fashion-MNIST数据集)
- 使用三种不同的激活函数,对比实验结果
- 使用不同的隐藏层层数和隐藏单元个数,对比实验结果
- 在上面实验中分别手动实现和利用torch.nn实现dropout,探究不同丢弃率对结果的影响
- 分别手动实现和利用torch.nn实现L2正则化,探究不同惩罚项权重对结果的影响
- 选择上述实验中效果最好的模型,采用10折交叉验证评估实验结果
一、利用torch.nn实现前馈神经网络
导入包和加载Fashion-MNIST数据集可参考之前的博客,下面直接开始构建模型的部分
# 3、构建模型
num_inputs = 784
num_outputs = 10 # 共10类
num_hiddens = 256
class FlattenLayer(torch.nn.Module): # Flatten层
def __init__(self):
super(FlattenLayer, self).__init__()
def forward(self, x):
return x.view(x.shape[0], -1)
class SoftmaxLayer(torch.nn.Module):
def __init__(self):
super(SoftmaxLayer, self).__init__()
def forward(self, X):
X_exp = X.exp() # 对每个元素做指数运算
partition = X_exp.sum(dim=1, keepdim=True) # 求列和,即对同行元素求和 n*1
return X_exp / partition # broadcast
net = torch.nn.Sequential(
FlattenLayer(),
torch.nn.Linear(num_inputs, num_hiddens),
# 下面是三种可选用的激活函数
torch.nn.ReLU(), # Relu激活函数
# torch.nn.Softplus(), # Softplus激活函数
# torch.nn.Tanh(), # Tanh激活函数
torch.nn.Linear(num_hiddens, num_outputs),
SoftmaxLayer(),
)
初始化模型参数
# 4、初始化模型参数
for params in net.parameters(): # 对网络中的每个参数
torch.nn.init.normal_(params, mean=0, std=0.01) # 初始化为服从均值0标准差0.01正态分布
损失函数与优化器
# 5、损失函数与优化器
num_epochs = 10 # 训练轮次
lr = 0.1
loss = torch.nn.CrossEntropyLoss() # 交叉熵损失函数
optimizer = torch.optim.SGD(net.parameters(), lr)
评估函数
# 评估函数
def evaluate(data_iter, net):
right_sum, n, loss_sum = 0.0, 0, 0.0
for x, y in data_iter:
y_ = net(x)
l = loss(y_, y).sum()
right_sum += (y_.argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
loss_sum += l.item()
return right_sum / n, loss_sum / n
模型训练与评估
train_l_ = []
test_l_ = []
train_acc_ = []
test_acc_ = []
def train(net, loss, num_epochs, optimizer, train_iter, test_iter):
for epoch in range(num_epochs):
train_r_num, train_l, n = 0.0, 0.0, 0
for X, y in tqdm(train_iter):
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
optimizer.zero_grad()
train_r_num += (y_hat.argmax(dim=1) == y).sum().item()
train_l += l.item()
n += y.shape[0]
test_acc, test_l = evaluate(test_iter, net)
train_l_.append(train_l / n)
train_acc_.append(train_r_num / n)
test_l_.append(test_l)
test_acc_.append(test_acc)
print('epoch %d, train loss %.4f, train acc %.3f' % (epoch + 1, train_l / n, train_r_num / n))
print('test loss %.4f, test acc %.3f' % (test_l, test_acc))
train(net, loss, num_epochs, optimizer, train_iter, test_iter)
绘制loss曲线以及准确率曲线
# 绘制函数
def draw_(x, train_Y, test_Y, ylabel):
plt.plot(x, train_Y, label='train_' + ylabel, linewidth=1.5)
plt.plot(x, test_Y, label='test_' + ylabel, linewidth=1.5)
plt.xlabel('epoch')
plt.ylabel(ylabel)
plt.legend() # 加上图例
plt.show()
# 绘制loss曲线
x = np.linspace(0, len(train_l_), len(train_l_))
draw_(x, train_l_, test_l_, 'loss')
draw_(x, train_acc_, test_acc_, 'accuracy')
二、对比三种不同的激活函数的实验结果
1、ReLu激活函数
| 训练结果 |
|---|
 |
| loss曲线 | acc曲线 |
|---|---|
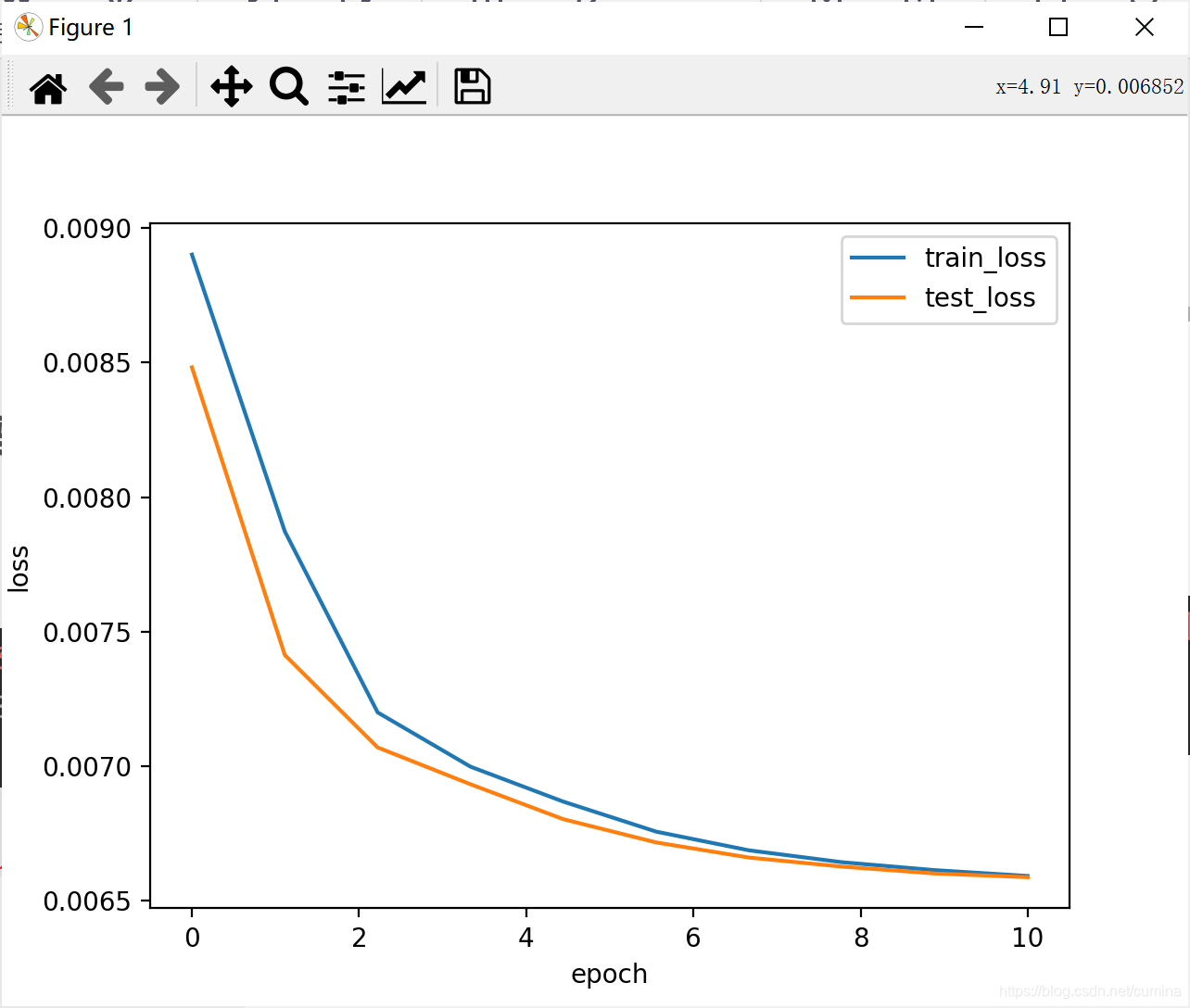 | 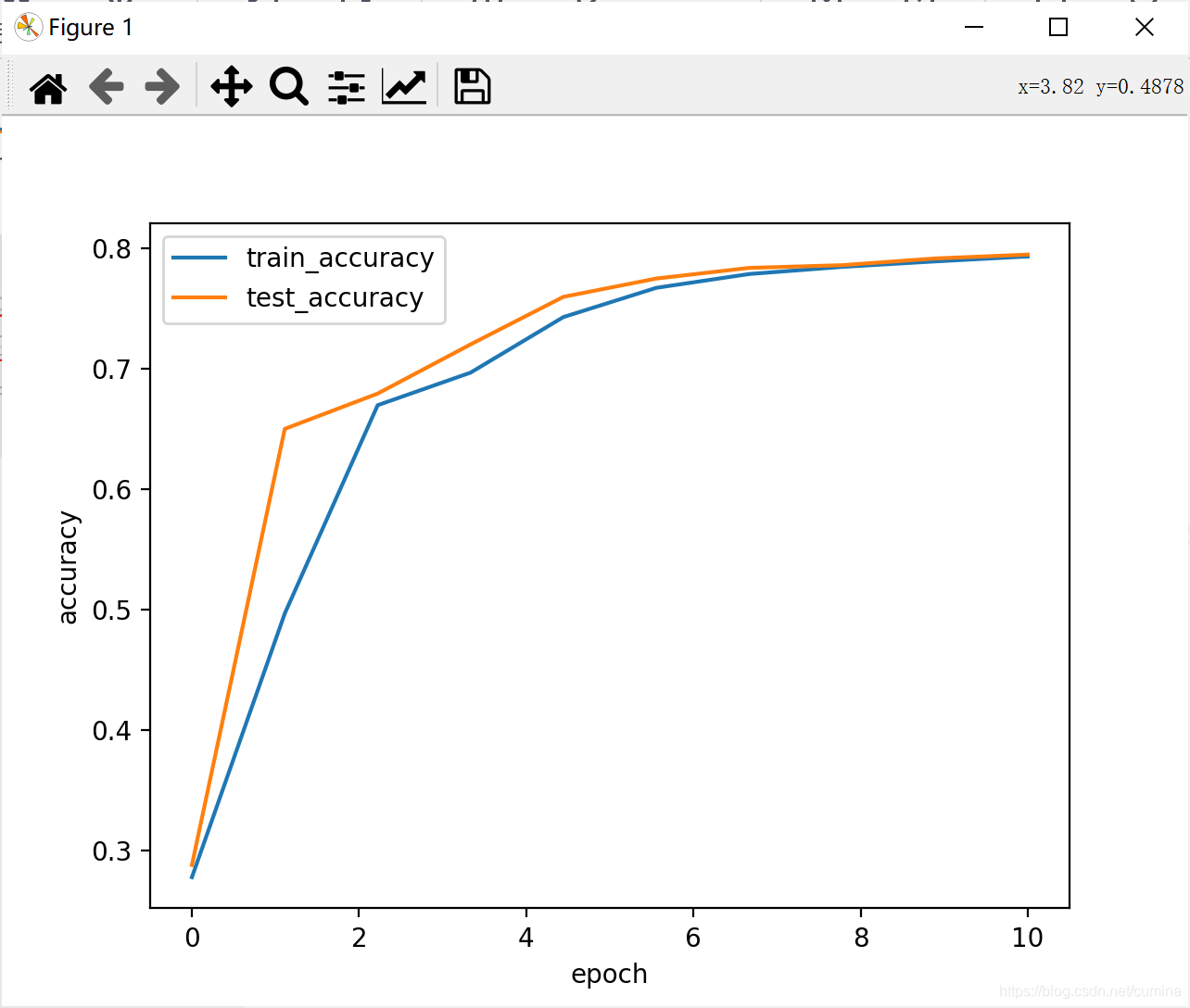 |
2、Softplus激活函数
| 训练结果 |
|---|
 |
| loss曲线 | acc曲线 |
|---|---|
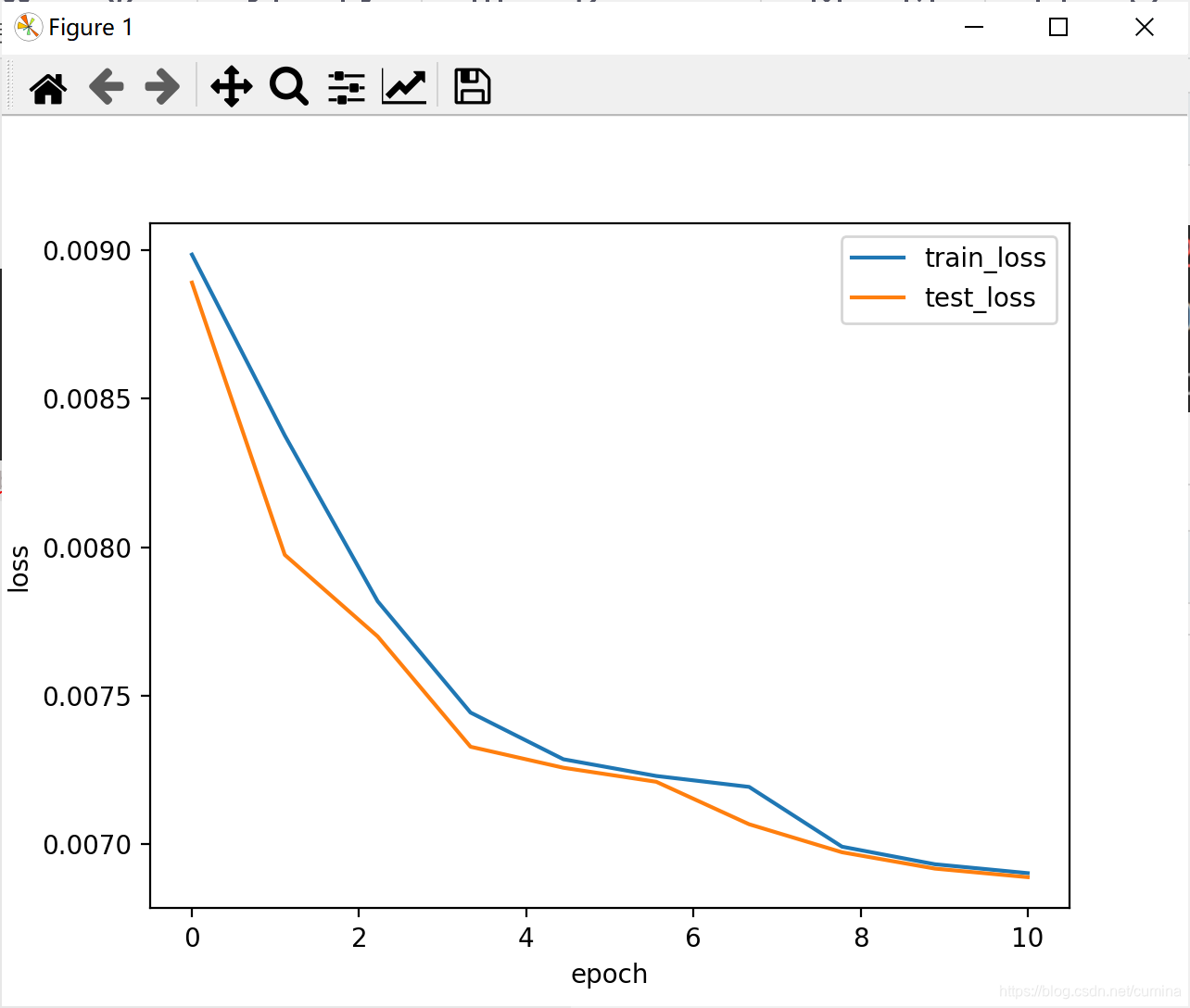 | 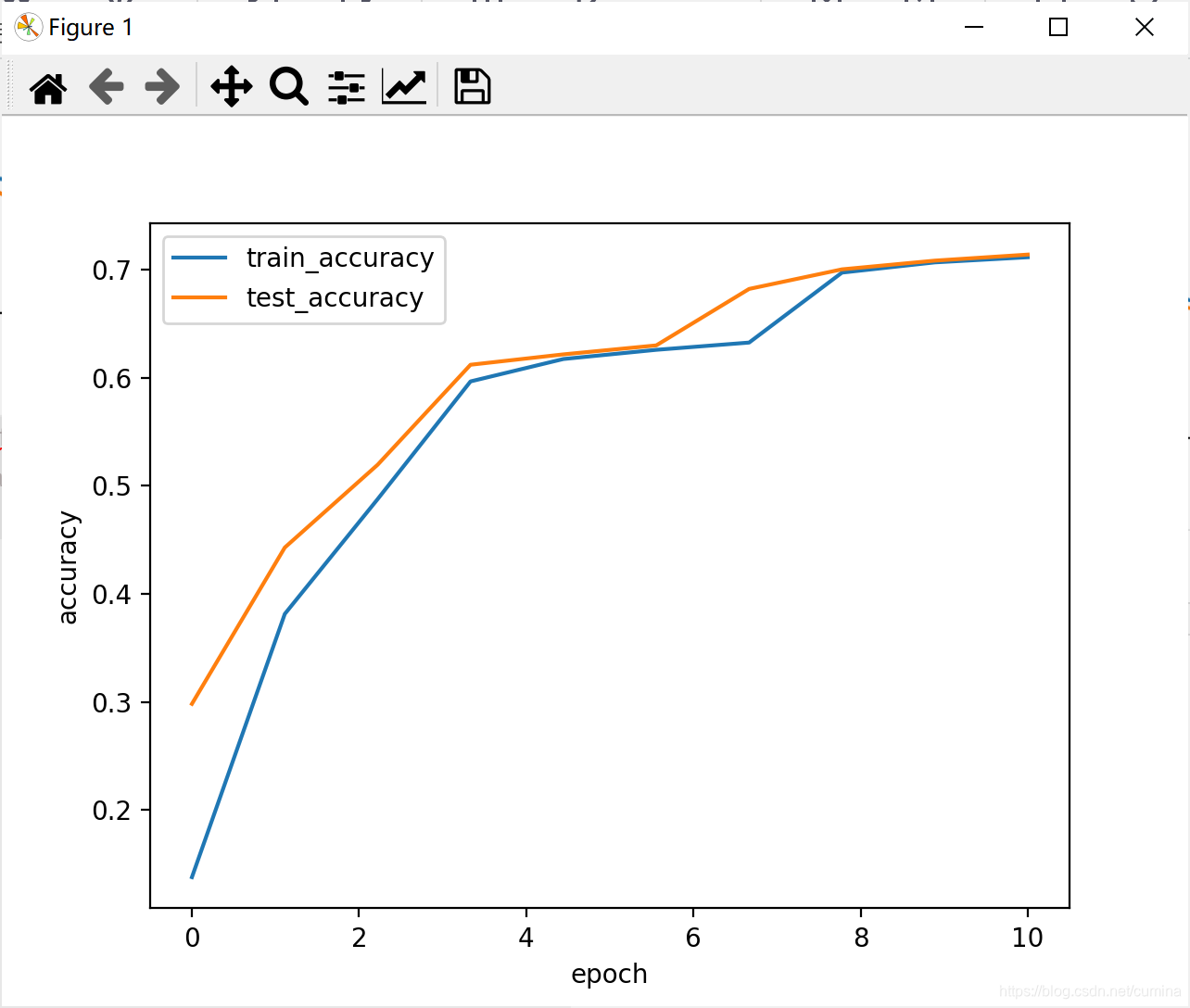 |
3、Tanh激活函数
| 训练结果 |
|---|
 |
| loss曲线 | acc曲线 |
|---|---|
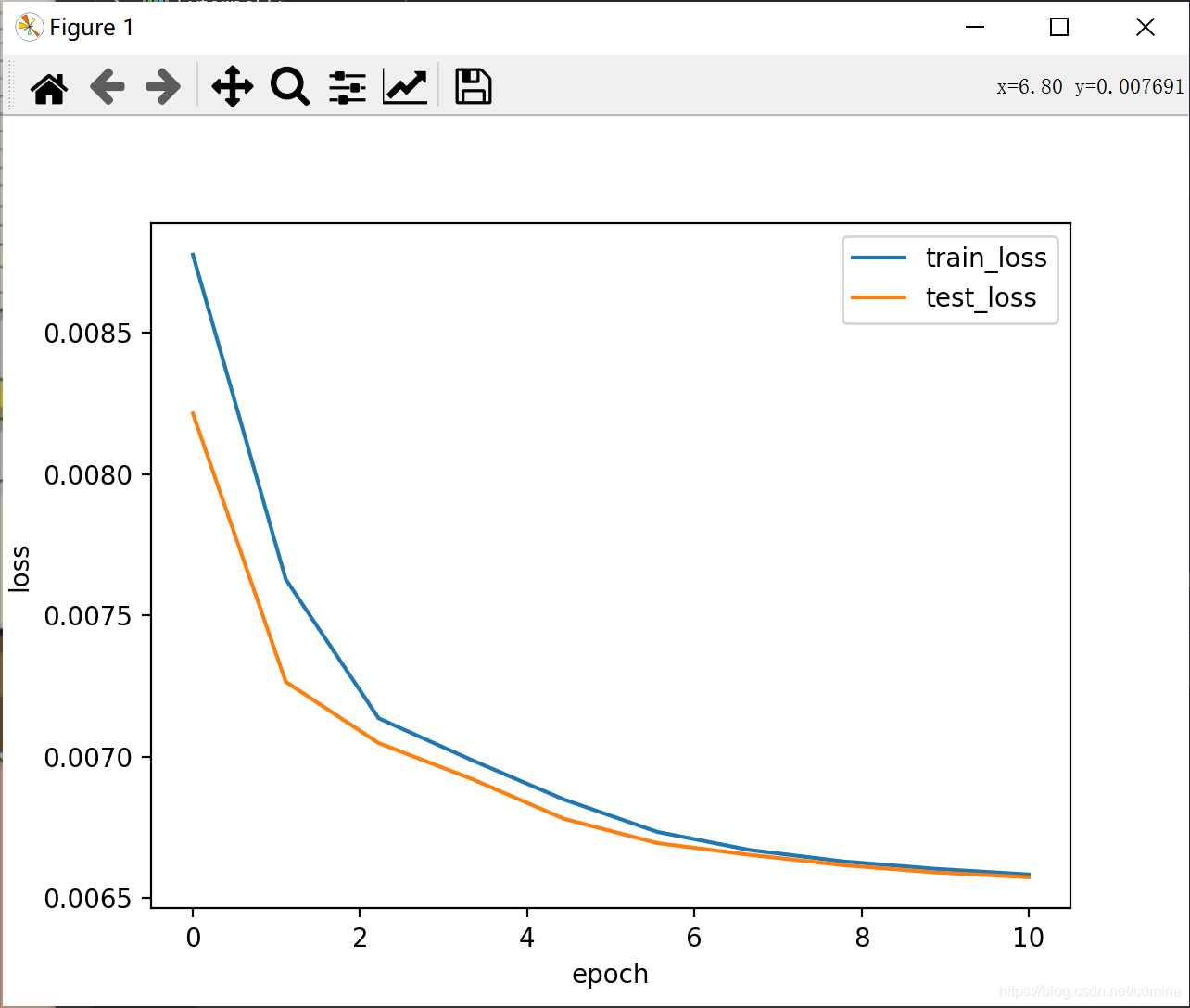 | 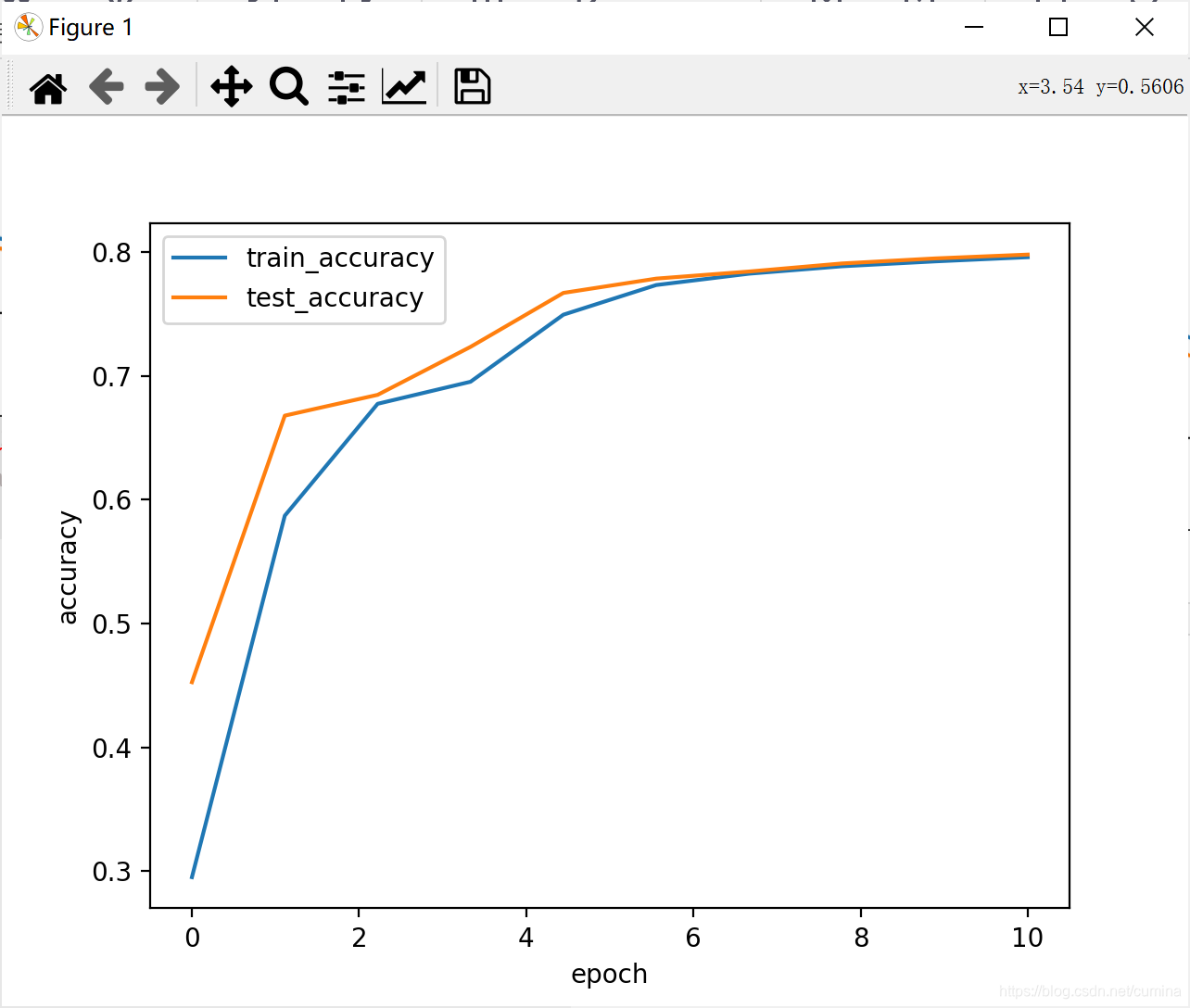 |
待续…