[人工智能]NLP文本相似度(TF-IDF)

前言

我们在比较事物时，往往会用到“不同”，“一样”，“相似”等词语，这些词语背后都涉及到一个动作——双方的比较。只有通过比较才能得出结论，究竟是相同还是不同。但是万物真的有这么极端的区分吗？在我看来不是的，生活中通过“相似度”这词来描述可能会更加准确。比如汽车和飞机，虽然原理及外形都不一样，但也有相同的地方，那就是都是交通工具，就是说相似度不为0；两个句子词和词的顺序都一致，相似度就是1。

数学基础

在介绍TF-IDF先了解下数学中的向量。

• 向量相加
  
  $$\left[\begin{array}{c}{x}_1\\ y_1\end{array}\right]+\left[\begin{array}{c}{x}_2\\ y_2\end{array}\right]=\left[\begin{array}{c}{x}_1+x_2\\ y_1+y_2\end{array}\right]=\left[\begin{array}{c}2+3\\ 4+1\end{array}\right]$$
• 向量和常量相乘
  
  $$\left[\begin{array}{c}x\\ y\end{array}\right]?2=\left[\begin{array}{c}2x\\ 2y\end{array}\right]$$
• 向量的夹角
  我们假设向量a、b起始点均在原点
  
  $$\cos \theta =\cos (\alpha ?\beta )=\cos (\alpha )\cos (\beta )+\sin (\alpha )\sin (\beta )=\frac{x_1}{\sqrt{x_1^2+y_1^2}}?\frac{x_2}{\sqrt{x_2^2+y_2^2}}+\frac{y_1}{\sqrt{x_1^2+y_1^2}}?\frac{y_2}{\sqrt{x_2^2+y_2^2}}$$
  $$\cos \theta =\frac{x_1{x}_2+y_1{y}_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}=\frac{a?b}{|a||b|}$$
  将坐标系转为n维度,即向量a为(x1,x2,x3…xn)向量b为(y1,y2,y3…yn)
  $$\cos \theta =\frac{{\sum }_{i=1}^n(x_i?y_i)}{\sqrt{{\sum }_{i=1}^n{x}_i^2}\sqrt{{\sum }_{i=1}^n{y}_i^2}}$$

原理介绍

我们可能把生活中的事务通过向量的形式描述。

这件衣服号码大了，那个号码适合
分词=》
(这件,衣服,号码,大了,那个,适合)
词频统计=》
(1,1,2,1,1,1)

到这里出现一个关键的名词——词频TF，词频是一个词语在文章或句子中出现的次数,上述仅号码出现了2次。再根据上述的cosθ公式可得。就能计算出两句话相似度了，即cosθ越小相似度越大。下面通过实际例子：

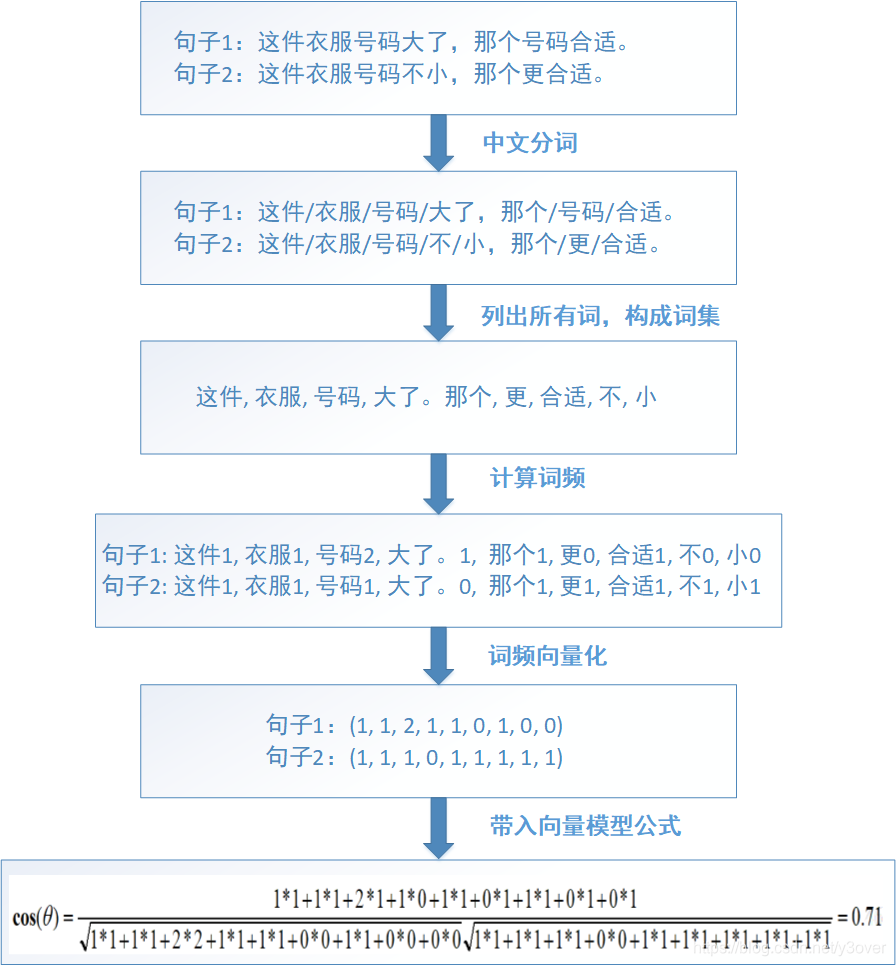
上述分析通过通过上述过程分析还存在以下问题

• 比如“地”，“的”，“啊”等词，它们出现的次数对一篇文章的中心思想没有一点帮助，词频又高，只是中文语法结构的一部分而已
• 比如，句子1：你真好看:。句子2：你真难看。这两句话相似度75%，但是它们的语义相差十万八千里，可以说是完全相反
• 比如如果想分析近期的十九届中央纪委二次全会等新闻文章，很明显出现“中国”这个词语必定会出现在每篇文章，但是对于每个新闻的主干思想有帮助吗？对比“反腐反败”，“人工智能”“大数据”等词语，“中国”这个词语在文章中应该是次要的

停用词过滤

针对问题1，我们把这些没有中心思想没有一点词归类并称为“停用词”。然后，在计算一篇文章的词频时，把停用词过滤掉的。

同义词转换

没有很完美的解决方案。每个公司根据业务将相同的词进行转换， 来调节相似度，使其在某些场合能够精确计算。

反文档频率IDF

针对问题3，在一篇文章或一个句子来说，对于每个词都有不同的重要性，这也就是词的权重。在词频的基础上，赋予每一个词的权重，进一步体现该词的重要性。比如一篇报道中国农业养殖的新闻报道。较常见的词（“国内”、“中国”、“报道”）给予较小的权重，较少见的词（“养殖”、“维基”）给于较大的权重。所以刻画能力强的词语，权重应该是最高的。因此，在词频TF的基础上又引出了反文档频率IDF的概念，表示即词在文章中的占比。下面是反文档频率的计算方法：

针对这个公式，可能有人会有以下的疑问：
1. 为什么+1？是为了处理分母为0的情况。假如所有的文章都不包含这个词，分子就为0，所以+1是为了防止分母为0的情况。
2. 为什么要用log函数？log函数是单调递增，求log是为了归一化，保证反文档频率不会过大。
3. 会出现负数？肯定不会，分子肯定比分母大。

结合词频的计算方法：

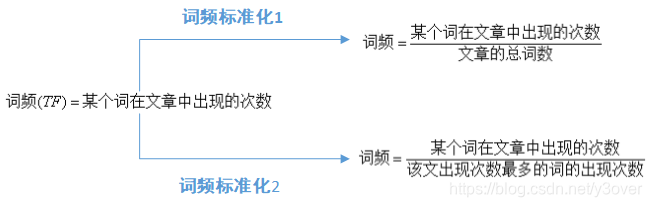
词频标准化的目的是把所有的词频在同一维度上分析。 第一种情况，得出词汇较小，不便于分析。一般情况下，第二个标准更适用，因为能够使词频的值相对大点，便于分析。比如一本书出现一个词语100次，但整本书10万字，词频但是在一句话中出现5次。

TF和IDF进行相乘,得到了一个词的TF-IDF值,某个词对文章重要性越高，该值越大.

TF-IDF = 计算的词频(TF)*计算的反文档频率(IDF)

通过公式可以知道，TF-IDF与在该文档中出现的次数成正比，与包含该词的文档数成反比。这样做的优点是简单快速，结果比较符合实际情况。缺点是单纯以“词频”做衡量标准，不够全面词性和词的出现位置等因素没有考虑到，这种算法无法体现词的位置信息，出现位置靠前的词与出现位置靠后的词，都被视为重要性相同，这是不正确的。

一种解决方法是，对全文的第一段和每一段的第一句话或者一此词，给予较大的权重。

TF-IDF是一种用于资讯检索与文本挖掘的常用加权技术，主要思想是：如果某个词或短语在一篇文章中出现的频率TF高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。

Lucene实用评分函数

Lucene 就会为查询计算评分，然后合并每个匹配词的评分结果。这里使用的评分计算公式叫做 实用评分函数（practical scoring function）

1. score(q,d), q为搜索词，d为文件
2. queryNorm(q)：查询归一因子试图将查询归一化，这样就能将两个不同的查询结果相比较. t表示q分词命中的词
3. coord(q,d)：协调因子可以为那些查询词包含度高的文档提供奖励，文档里出现的查询词越多，它越有机会成为好的匹配结果。
4. 查询 q 中每个词 t 对于文档 d 的权重和。
5. tf(t in d)：Term t在文档d中出现的词频
6. idf(t)：是词 t 的 逆向文档频率
7. t.getBoost() 是词 t 查询中使用的权重
8. norm(t,d)即建文档时对一此词的权重设置
   

• Document boost：文档权值越大，说明此文档越重要。
• Field boost：域权值越大，说明此域越重要。
• lengthNorm(field) = (1.0 / Math.sqrt(numTerms))：一个域中包含的Term总数越多，也即文档越长，此值越小，文档越短，此值越大。

让我们忽略所有的boost，因为这些属于人为的调整，得到真正的打分公式如下

上述公式的求证过程如下：

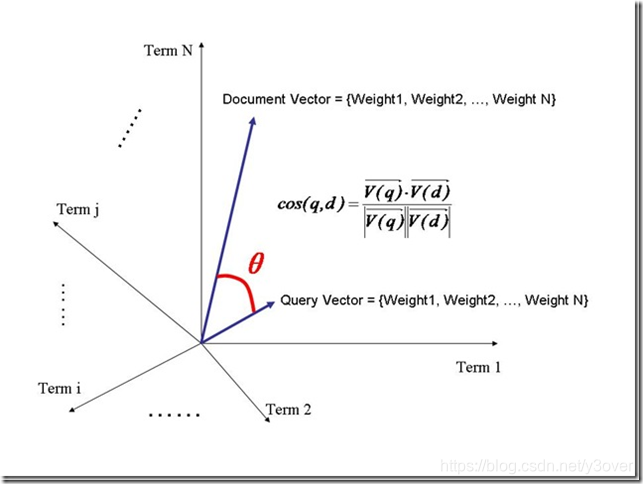
• 把所有此文档d中词(term)的权重(term weight) 看作一个向量

Document = {term1, term2, …… ,term N}
Document Vector = {weight1, weight2, …… ,weight N}

• 把查询语句也用向量来表示

Query = {term1, term 2, …… , term N}
Query Vector = {weight1, weight2, …… , weight N}

• 所有搜索出的文档向量及查询向量放到一个N维空间中，每个词(term)是一维，并代入两个向量之间的夹角公式
• 首先计算余弦公式的分子部分

Vq*Vd = w(t1, q)*w(t1, d) + w(t2, q)*w(t2, d) + …… + w(tn ,q)*w(tn, d)

• 再根据权重w=tf*idf

Vq*Vd = tf(t1, q)*idf(t1, q)*tf(t1, d)*idf(t1, d) + tf(t2, q)*idf(t2, q)*tf(t2, d)*idf(t2, d) + …… + tf(tn ,q)*idf(tn, q)*tf(tn, d)*idf(tn, d)

• 在查询的时候，很少有人会在查询语句中输入同样的词，因而可以假设tf(t, q)都为1
• idf是指Term在多少篇文档中出现过，其中也包括查询语句这篇小文档，因而idf(t, q)和idf(t, d)其实是一样的，是索引中的文档总数加一，当索引中的文档总数足够大的时候，查询语句这篇小文档可以忽略，因而可以假设idf(t, q) = idf(t, d) = idf(t)

Vq*Vd = tf(t1, d) * idf(t1) * idf(t1) + tf(t2, d) * idf(t2) * idf(t2) + …… + tf(tn, d) * idf(tn) * idf(tn)

• 代入余弦公式变为：
  
• 查询语句中tf都为1，得|Vq|
  
• 代入余弦公式变为：
  
• 关于|Vq|

• 因为在索引中，不同的文档长度不一样，很显然，对于任意一个term，在长的文档中的tf要大的多，因而分数也越高，这样对小的文档不公平.
  举一个极端的例子，在一篇1000万个词的鸿篇巨著中，"lucene"这个词出现了11次，而在一篇12个词的短小文档中，"lucene"这个词出现了10次，如果不考虑长度在内，当然鸿篇巨著应该分数更高，然而显然这篇小文档才是真正关注"lucene"的。
• 然而如果按照标准的余弦计算公式，完全消除文档长度的影响，则又对长文档不公平(毕竟它是包含了更多的信息)，偏向于首先返回短小的文档的，这样在实际应用中使得搜索结果很难看。
• 所以在Lucene中，Similarity的lengthNorm接口是开放出来，用户可以根据自己应用的需要，改写lengthNorm的计算公式。
  比如我想做一个经济学论文的搜索系统，经过一定时间的调研，发现大多数的经济学论文的长度在8000到10000词，因而lengthNorm的公式应该是一个倒抛物线型的，8000到 10000词的论文分数最高，更短或更长的分数都应该偏低，方能够返回给用户最好的数据。
• 在默认状况下，Lucene采用DefaultSimilarity，认为在计算文档的向量长度的时候，每个Term的权重就不再考虑在内了，而是全部为1。而从Term的定义我们可以知道，Term是包含域信息的，也即title:hello,content:hello是不同的Term，也即一个Term只可能在文档中的一个域中出现。
  

• 代入余弦公式：
  

主要参考

《向量是什么——线性代数本质》
《两个向量之间的夹角公式》
《NLP文本相似度(TF-IDF)》
《Lucene学习总结之六：Lucene打分公式的数学推导》
《Elasticsearch: 权威指南之Lucene 的实用评分函数》