一.LinearRegression().score方法
关于LinearRegression().score(self, X, y, sample_weight=None)方法,官方描述为:
Returns the coefficient of determination R^2 of the prediction.
The coefficient R^2 is defined as (1???(u)/(v)), where u is the residual sum of squares ((y_true - y_pred) ** 2).sum() and v is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R2 score of 0.0.
其返回值为决定系数R^2,计算公式为:
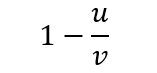
其中u的计算公式为:
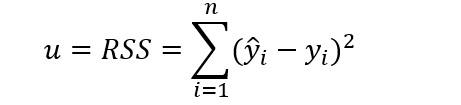
RSS为residual sum of squares即残差平方和。
其中v的计算公式为:
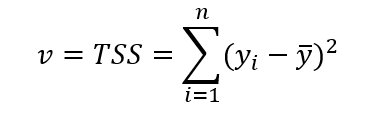
TSS为total sum of squares,即总体平方差
其中,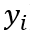 是实际的观察值,
是实际的观察值, ![[公式]](https://img-blog.csdnimg.cn/82117b90985f4df5b90d854199e9c1aa.png) 是模型预测的输出值。
是模型预测的输出值。 ![[公式]](https://img-blog.csdnimg.cn/0d75a163d2f140e59c4b8cb9199dd8b5.png) 是表示的是所有观察值的均值。
是表示的是所有观察值的均值。
二.决定系数
在统计学中,决定系数反映了因变量y 的波动,有多少百分比能被自变量x(用机器学习的术语来说, x 就是特征)的波动所描述。简单来说,该参数可以用来判断统计模型对数据的拟合能力(或说服力)。

于是,**回归残差(residual)**可定义为:

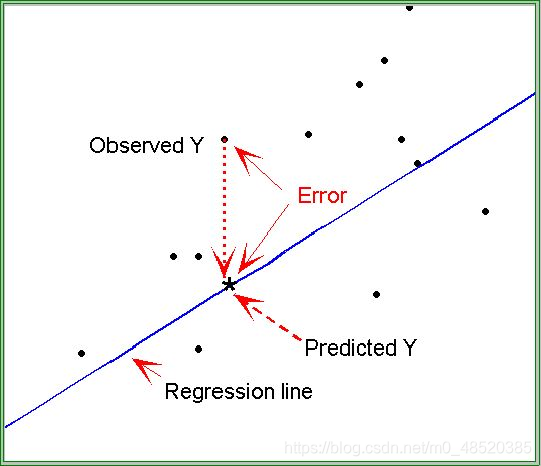
那么,平均观察值可定义为:

于是,总体离差平方和(Sum of Squares for total,亦简称SST)为:
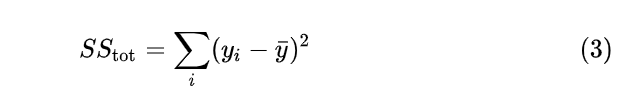
回归平方和(Sum of Squares for regression,简称亦SSR)为:

请注意公式(3)和公式(4)的差别。
其中,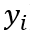 是实际的观察值,
是实际的观察值, ![[公式]](https://img-blog.csdnimg.cn/82117b90985f4df5b90d854199e9c1aa.png) 是模型预测的输出值。
是模型预测的输出值。 ![[公式]](https://img-blog.csdnimg.cn/0d75a163d2f140e59c4b8cb9199dd8b5.png) 是表示的是公式(2)呈现的均值。
是表示的是公式(2)呈现的均值。
用数学语言简单描述,决定系数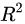 就是回归平方和与总平方和之比,其表达式为:
就是回归平方和与总平方和之比,其表达式为:
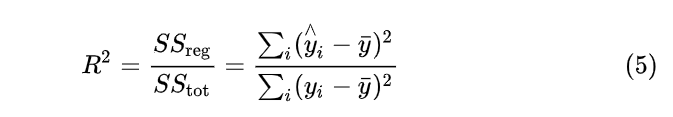
也可写为
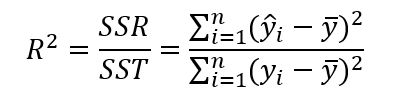
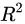 取值在0到1之间,其数值大小反映了回归贡献的相对程度,即在因变量Y的总变异中,回归关系所能解释的百分比。R2是最常用于评价回归模型优劣程度的指标。
取值在0到1之间,其数值大小反映了回归贡献的相对程度,即在因变量Y的总变异中,回归关系所能解释的百分比。R2是最常用于评价回归模型优劣程度的指标。
事实上, ![[公式]](https://img-blog.csdnimg.cn/b8c7c25b992145bebd8949310b248707.png) (即SST)刻画的误差,可分为两部分。一部分来自于我们拟合出来的模型,用它刻画数据的变异差值,即
(即SST)刻画的误差,可分为两部分。一部分来自于我们拟合出来的模型,用它刻画数据的变异差值,即 ![[公式]](https://img-blog.csdnimg.cn/b84e4117bc9e4a449efa7c8c7e4855fc.png) (即SSR),另一部分是模型本身带来的误差,即:残差平方和(residual sum of squares,简称RSS),它的定义为:
(即SSR),另一部分是模型本身带来的误差,即:残差平方和(residual sum of squares,简称RSS),它的定义为:
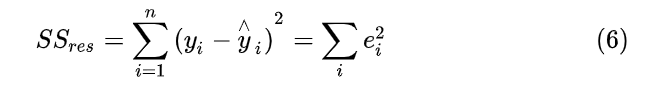
也就是说,
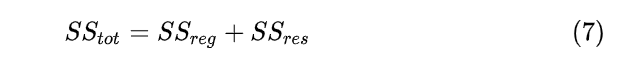
结合公式(5)和(7),推导可得![[公式]](https://img-blog.csdnimg.cn/2a8dd6b1438a4474859b778b620896e3.png) 表达式:
表达式:

通常来说,对于训练数据集来说, ![[公式]](https://img-blog.csdnimg.cn/60b0828fcca3471095cadaf9ab207804.png) 取值范围介于[0,1]。对于测试集合而言,其值还可能为负值。一般而言,
取值范围介于[0,1]。对于测试集合而言,其值还可能为负值。一般而言, ![[公式]](https://img-blog.csdnimg.cn/abc4df7249994d9a83fb2fa4b3747882.png) 越高,说明自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。
越高,说明自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。
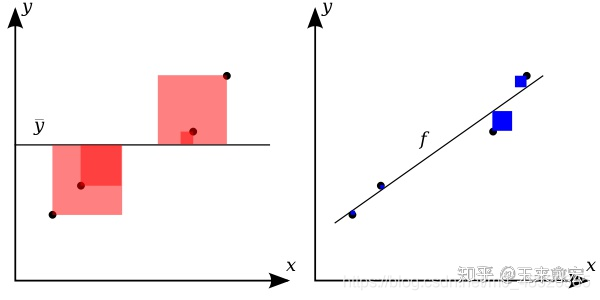
如图2所示,线性回归(右侧子图)的拟合效果很好,蓝色方块的边长代表残差大小,蓝色方块的面积就是残差的平方,很显然,蓝色方块越小,残差就越小,说明拟合的效果越棒!
观察可知,如果 ![[公式]](https://img-blog.csdnimg.cn/e8a9947575974251971c07a721ed2cd7.png) 。所以由公式(8)可得到,决定系数的值趋近于1。
。所以由公式(8)可得到,决定系数的值趋近于1。
相比而已,图2的右侧子图 红色正方形,它的边长表示因变量(y )相比于均值( ![[公式]](https://img-blog.csdnimg.cn/cea6d808629a4f68b5683e37ec567243.png) )的差异程度,于是,红色方块的面积就是方差。它用于刻画数据本身的波动特征。
)的差异程度,于是,红色方块的面积就是方差。它用于刻画数据本身的波动特征。
反之,R2的值越小,说明拟合程度越差。
对于R2我们需要注意:
1.R2 -般用在线性模型中(虽然非线性模型总也可以用)
2. R2不能完全反映模型预测能力的高低
但具体问题还得具体分析。对时间序列数据, ![[公式]](https://img-blog.csdnimg.cn/3111535e56204d23bca0a2c318759b1c.png) 达到0.9以上亦属稀疏平常;但对截面数据而言,能够达到0.5就已难能可贵了。
达到0.9以上亦属稀疏平常;但对截面数据而言,能够达到0.5就已难能可贵了。
在Scikit-learn中,回归模型的性能分数,就是利用 ![[公式]](https://img-blog.csdnimg.cn/7289512ca52a4abb9dd7eab06df0e7dc.png)
对拟合效果打分的,具体方法是,在性能评估模块中,通过一个叫做score()函数实现的,请参考下面的范例。
三.预测糖尿病实例(使用拟合度评估)
在下面的范例中,我们将分别查看在训练集和测试集中的决定系数。
我们使用皮马印第安人糖尿病数据集(pima Indians Diabetes Data Set)测试。这也是Scikit-learn中一个内置的经典数据集。
在该数据集中,包括442个病人的生理数据及一年以后的病情发展情况。
数据集中的特征值总共10项:年龄、性别、体质指数、血压、s1~s6(6种血清的化验数据)。但需要注意的,以上的数据是经过预处理, 10个特征都做了归一化处理。
第11项数据,是我们的要预测的目标值,一年疾后的病情定量测量,它是一个连续的实数值,符合线性回归模型评估的范畴。
我们可以利用sklearn的常用操作来了解这个数据集合的更多信息。在成功安装Scikit-Learn软件包,只用如下指令即可完成数据的加载:
from sklearn.datasets import load_diabetes #导入pima数据的API
pima = load_diabetes() #导入数据
print(pima.keys()) #输出该数据集相关的key。
运行上述代码,得到结果是:
dict_keys([‘data’, ‘target’, ‘frame’, ‘DESCR’, ‘feature_names’, ‘data_filename’, ‘target_filename’])
需要指出的是,在Scikit-Learn中,所有内置数据集都有data, target, frame, DESCR, feature_names这5个关键字(key),其中,data并不是泛指数据,而是在狭义上指除标签之外的特征数据,针对pima数据集,它指的是前面的10个特征值。
【输出结果】
[[ 0.03807591 0.05068012 0.06169621 … -0.00259226 0.01990842
-0.01764613]
[-0.00188202 -0.04464164 -0.05147406 … -0.03949338 -0.06832974
-0.09220405]
[ 0.08529891 0.05068012 0.04445121 … -0.00259226 0.00286377
-0.02593034]
…
[ 0.04170844 0.05068012 -0.01590626 … -0.01107952 -0.04687948
0.01549073]
[-0.04547248 -0.04464164 0.03906215 … 0.02655962 0.04452837
-0.02593034]
[-0.04547248 -0.04464164 -0.0730303 … -0.03949338 -0.00421986
0.00306441]]
如果我们想输出第一条数据的第三个特征,就用
即可完成数据的输出:
print(pima.data[0][2])
【输出结果】
0.0616962065186885
如果对这个数据集合比较陌生,或许你想知道,data数据集合中的每条数据都有10个特征,它们分别是什么意思呢?这里我们可以用输出feature_names这个关键字来看看它们的含义:
print(pima.feature_names)
【输出结果】
[‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’]
言归正转。下面我们用这个数据集来评估一下线性回归在训练集合和测试集合的『决定系数』,从而在某种程度上推断,拟合的模型是否过拟合了。
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import numpy as np
from sklearn.metrics import r2_score
#(1)导入数据
X, y = load_diabetes().data, load_diabetes().target
#(2)分割数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)
#(3)训练
LR = LinearRegression()
performance = LR.fit(X_train, y_train)
#(4)预测(本例分必要)
y_pred_train = LR.predict(X_train) #在测试集合上预测
y_pred_test = LR.predict(X_test) #在测试集合上预测
#(5) 评估模型
print("训练集合上R^2 = {:.3f}".format(performance.score(X_train, y_train)))
print("测试集合上R^2 = {:.3f} ".format(performance.score(X_test, y_test)))
print("训练集合上R^2 = {:.3f}".format(r2_score(y_train, y_pred_train)))
print("测试集合上R^2 = {:.3f} ".format(r2_score(y_test,y_pred_test)))
#控制数组的输出方式
np.set_printoptions(precision=3, suppress=True)
#对于线性回归和逻辑回归,其目标函数为:
# g(x) = w1x1 + w2x2 + w3x3 + w4x4 + w0
# 如果有激活函数sigmoid,增加非线性变化 则为分类 即逻辑回归
# 如果没有激活函数,则为回归
# 对于这样的线性函数,都会有coef_和intercept_函数
print('w0 = {0:.3f}'.format(LR.intercept_))#coef_和intercept_都是模型参数,即为w,intercept_为w1-w10
print('W = {}'.format(LR.coef_))#coef_为w0
训练集合上R^2 = 0.555
测试集合上R^2 = 0.359
训练集合上R^2 = 0.555
测试集合上R^2 = 0.359
w0 = 153.068
W = [ -43.268 -208.671 593.398 302.898 -560.277 261.477 -8.833 135.937
703.227 28.348]
在本例中,我们利用了Scikit-learn中的普通线性规划模型。从运行结果可以看出,训练集合的拟合优度R2(0.555)高于测试集合(0.359),这是符合预期的。
简单来说,R2→1模型的数据拟合性就越好,反之,R2→0,表明模型的数据拟合度越差。
但如果测试集合和训练集合这二者的R2值差别如果过大,则我们有理由怀疑,训练出来的模型存在一定程度上的过拟合。
此外,我们还可以看到,在模型的评估部分,在训练集合上,performance.score(X_train, y_train))和r2_score(y_train, y_pred_train))的输出结果是一致的。在测试结合上,亦是如此。
这表明,Scikit-learn框架中,性能评估的分数(Score),其实使用的就是『决定系数』
参考网址:
https://zhuanlan.zhihu.com/p/67706712
https://www.cnblogs.com/jiangkejie/p/10677858.html