写在前面
今天主要探索的是改变神经网络的权重和阈值的初始值的大小对于模型输出结果的影响,本篇文章首先会介绍一下我对输入数值的归一化处理,然后再通过示例查看初始化参数对于模型输出的影响。
归一化
为了减小MNIST数据本身数值大小的影响,我将MNIST图片的像素数据进行了归一化处理,归一化公式如下图所示:

程序实现如下图所示,需要注意的是,在程序中,我为了减小数字的位数,我将归一化数值进行了放大100倍的操作:
def normalization(x):
max = 0
min = 999
for i in range(0, 784):
if (x[i] > max):
max = x[i]
elif (x[i] < min):
min = x[i]
for i in range(0, 784):
x[i] = (x[i] - min) / (max - min) * 100
# print(x)
return x
探索
我是将一幅图像进行不断地训练,从而进行调优,因此我只取了MNIST数据集的第一张,也就是数字“5”进行预训练,看看我的神经网络模型是否有错,同时初步探索参数对于神经网络的影响。

下图是初始化了学习率为0.8, 对数字“5”训练200次,权重和阈值参数初始化的范围是(0, 0.4)得出的结果,乍看之下曲线形状还行,但是损失函数最低只能降到8左右,这显然是我们所不能接收的,但是目前还没有找出原因。
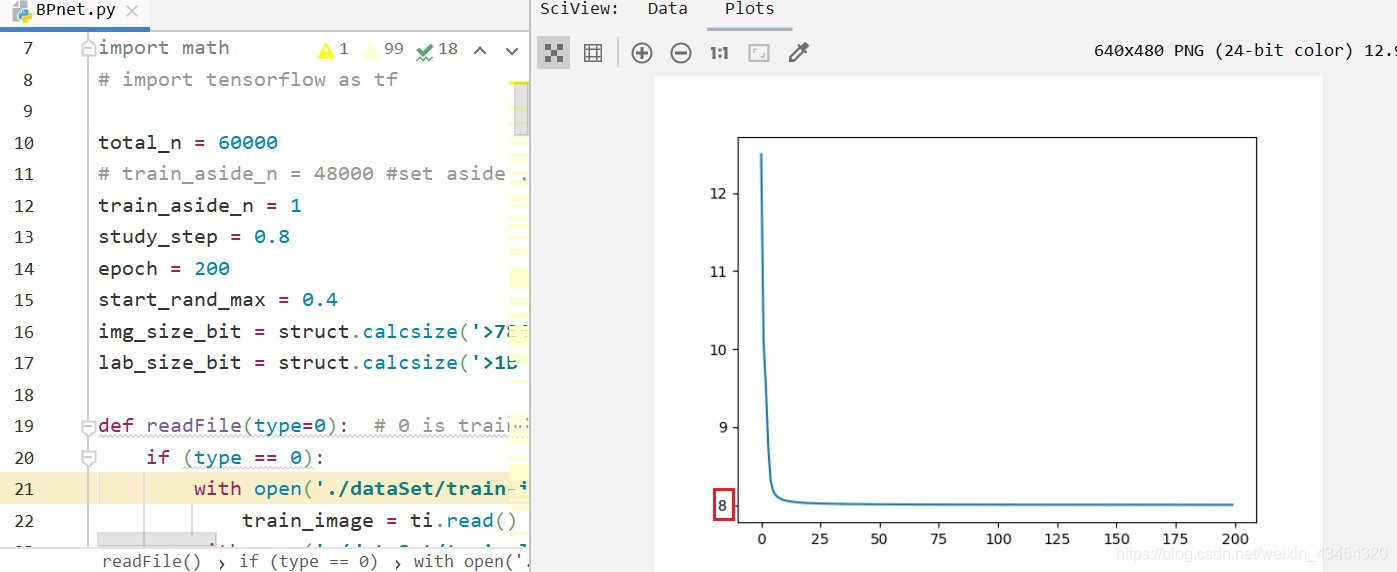
而且上图中曲线很丝滑是因为这是我调整过的参数,当我把参数打乱时,再来看看结果。
基于之前的数据,我将学习率调整成了0.04,曲线如下图所示:
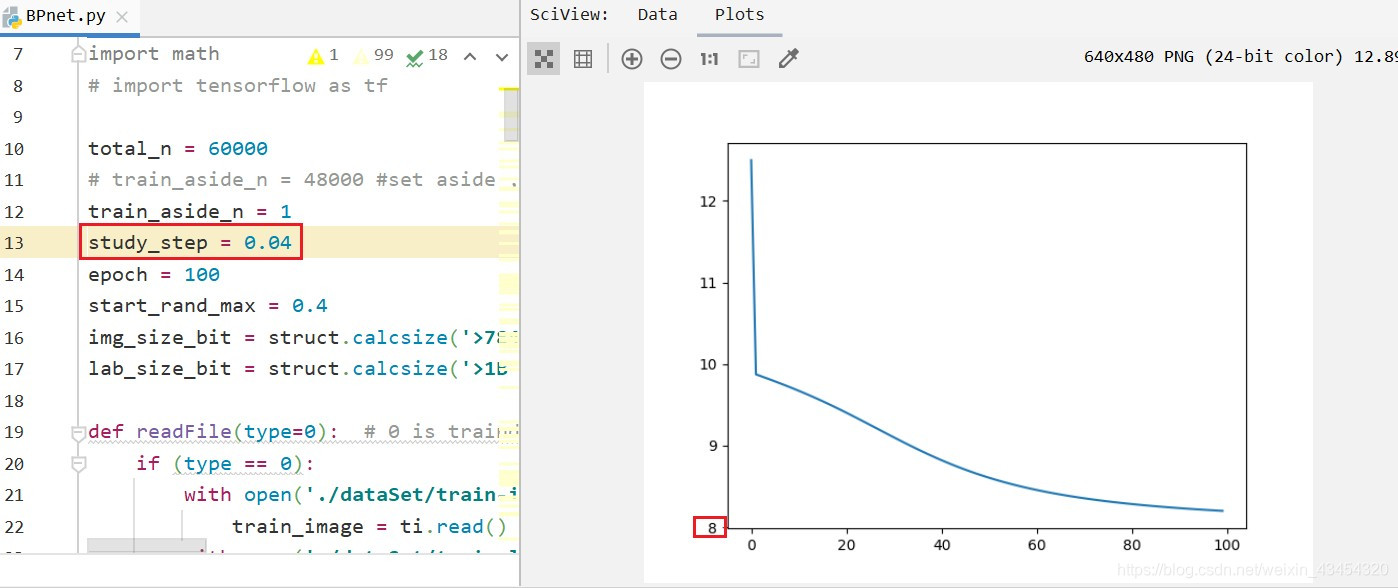
可以发现,损失函数的最小值不但没有变化,而且曲线也没那么好看了,这个就是学习率的影响。
权重和阈值的初始化方法:
w = np.zeros(((2,4)), dtype=float)#(()) is used to confirm line and row
gamma = np.zeros((4,1), dtype=float)
v = np.zeros((4,4), dtype=float)
theta_1 = np.zeros(((1,4)), dtype=float)
theta_2 = np.zeros(((1,4)), dtype=float)
theta_3 = random.uniform(0,start_rand_max)
m = np.ones(((1,4)), dtype=float)
n = np.ones(((1,4)), dtype=float)
input_x = np.zeros(((1, 2)), dtype=float)
y_out = float(0)
# init para
for i in range(0, 4): # [1,4]
gamma[i] = random.uniform(0,start_rand_max)
theta_1[0][i] = random.uniform(0,start_rand_max)
theta_2[0][i] = random.uniform(0,start_rand_max)
for j in range(0, 4):
v[i][j] = random.uniform(0,start_rand_max)
for k in range(0, 2):
w[k][i] = random.uniform(0, start_rand_max)
接下来我们来看看权重和阈值的初始值对于模型的输出影响。
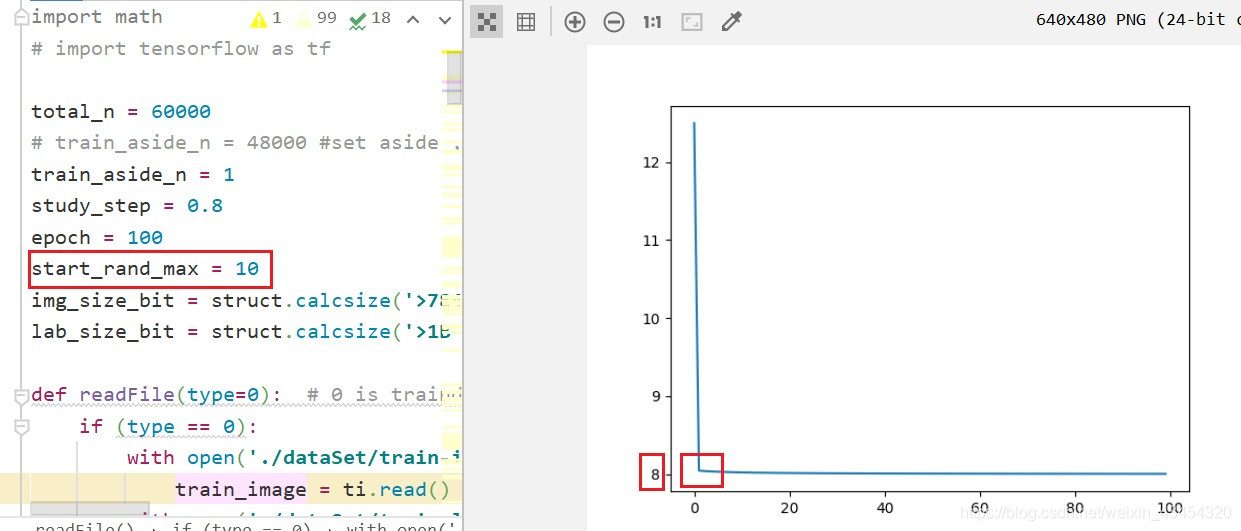
我将权重和阈值的随机初始化的范围改为了(1,10),模型的输出曲线同样产生了较大的变化,首先是曲线拐点出现了折点,目前没有搞明白是为啥,但是我觉得可能和数据大小有关系。
因为我归一化输入之后又进行了放大,因此输出数组的数值大小应该是在(1,100)之内的,所以我猜测神经网络的权重和阈值的数量级和输入变量的数量级差别较大时,模型的输出可能会受到较大的影响。
而且可以看到更改了权重和阈值的随机初始化的范围之后,损失函数的最小值并没有很明显的变化。

