[人工智能]数据预处理的一些小技巧

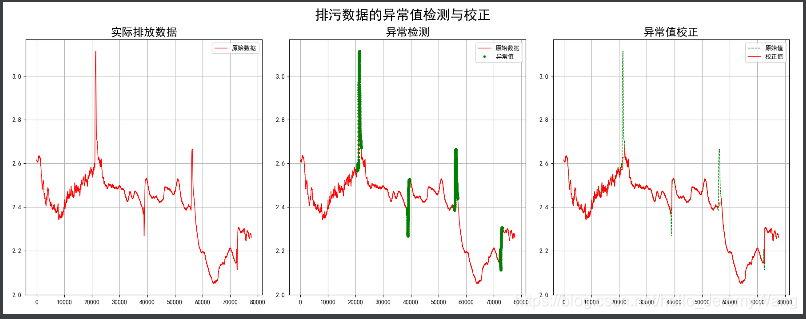
1. 时序数据的异常值处理

在本节，我们将介绍如何利用机器学习模型对时序数据进行异常值处理。我们以下图为例进行介绍，左一表示的是原始的时序数据，而中间一图中的绿色部分表示其中出现异常的点。在本节中，我们利用Bagging模型对异常的数据进行预测，从而替代原先异常的点。最终，我们可以得到右图中的数据分布。明显的，这个数据更加合理。

上述处理的代码如下：

import numpy as np
import matplotlib as mpl
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor


def read_data():
    plt.figure(figsize=(13, 7), facecolor='w')
    plt.subplot(121)
    data = pd.read_csv('C0904.csv', header=0)
    x = data['H2O'].values
    plt.plot(x, 'r-', lw=1, label=u'C0904')
    plt.title(u'实际排放数据0904', fontsize=18)
    plt.legend(loc='upper right')
    plt.grid(b=True)

    plt.subplot(122)
    data = pd.read_csv('C0911.csv', header=0)
    x = data['H2O'].values
    plt.plot(x, 'r-', lw=1, label=u'C0911')
    plt.title(u'实际排放数据0911', fontsize=18)
    plt.legend(loc='upper right')
    plt.grid(b=True)

    plt.tight_layout(2, rect=(0, 0, 1, 0.95))
    plt.suptitle(u'如何找到下图中的异常值', fontsize=20)
    plt.show()


if __name__ == "__main__":
    mpl.rcParams['font.sans-serif'] = [u'simHei']
    mpl.rcParams['axes.unicode_minus'] = False

    # read_data()
    data = pd.read_csv('C0904.csv', header=0)   # C0911.csv, C0904.csv
    x = data['H2O'].values
    print (x)

    width = 500
    delta = 10
    eps = 0.15
    N = len(x)
    p = []
    abnormal = []
    for i in np.arange(0, N-width, delta):
        s = x[i:i+width]
        p.append(np.ptp(s))
        if np.ptp(s) > eps:
            abnormal.append(range(i, i+width))
    abnormal = np.array(abnormal).flatten()
    abnormal = np.unique(abnormal)
    # plt.plot(p, lw=1)
    # plt.grid(b=True)
    # plt.show()

    plt.figure(figsize=(18, 7), facecolor='w')
    plt.subplot(131)
    plt.plot(x, 'r-', lw=1, label=u'原始数据')
    plt.title(u'实际排放数据', fontsize=18)
    plt.legend(loc='upper right')
    plt.grid(b=True)

    plt.subplot(132)
    t = np.arange(N)
    plt.plot(t, x, 'r-', lw=1, label=u'原始数据')
    plt.plot(abnormal, x[abnormal], 'go', markeredgecolor='g', ms=3, label=u'异常值')
    plt.legend(loc='upper right')
    plt.title(u'异常检测', fontsize=18)
    plt.grid(b=True)

    # 预测
    plt.subplot(133)
    select = np.ones(N, dtype=np.bool)
    select[abnormal] = False
    t = np.arange(N)
    dtr = DecisionTreeRegressor(criterion='mse', max_depth=10)
    br = BaggingRegressor(dtr, n_estimators=10, max_samples=0.3)
    br.fit(t[select].reshape(-1, 1), x[select])
    y = br.predict(np.arange(N).reshape(-1, 1))
    y[select] = x[select]
    plt.plot(x, 'g--', lw=1, label=u'原始值')    # 原始值
    plt.plot(y, 'r-', lw=1, label=u'校正值')     # 校正值
    plt.legend(loc='upper right')
    plt.title(u'异常值校正', fontsize=18)
    plt.grid(b=True)

    plt.tight_layout(1.5, rect=(0, 0, 1, 0.95))
    plt.suptitle(u'排污数据的异常值检测与校正', fontsize=22)
    plt.show()

2. 独热编码

对于定性变量，我们通常有两种编码形式。一种就是直接将其编为1,2,3,4…但是这种编码方式无形中给不同类型进行了排序，这对于无序的数据是不能接受的。独热编码就很好地解决了这个问题。
下面是独热编码的一个实例：

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegressionCV
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
import matplotlib as mpl
import matplotlib.pyplot as plt


if __name__ == '__main__':
    pd.set_option('display.width', 300)
    pd.set_option('display.max_columns', 300)

    data = pd.read_csv('car.data', header=None)
    n_columns = len(data.columns)
    columns = ['buy', 'maintain', 'doors', 'persons', 'boot', 'safety', 'accept']
    new_columns = dict(zip(np.arange(n_columns), columns))
    data.rename(columns=new_columns, inplace=True)
    print (data.head(10))

    # one-hot编码
    x = pd.DataFrame()
    for col in columns[:-1]:
        t = pd.get_dummies(data[col])
        t = t.rename(columns=lambda x: col+'_'+str(x))
        x = pd.concat((x, t), axis=1)
    print (x.head(10))
    # print x.columns
    y = pd.Categorical(data['accept']).codes

    x, x_test, y, y_test = train_test_split(x, y, train_size=0.7)
    clf = LogisticRegressionCV(Cs=np.logspace(-3, 4, 8), cv=5)
    clf.fit(x, y)
    print (clf.C_)
    y_hat = clf.predict(x)
    print ('训练集精确度：', metrics.accuracy_score(y, y_hat))
    y_test_hat = clf.predict(x_test)
    print ('测试集精确度：', metrics.accuracy_score(y_test, y_test_hat))
    n_class = len(data['accept'].unique())
    y_test_one_hot = label_binarize(y_test, classes=np.arange(n_class))
    y_test_one_hot_hat = clf.predict_proba(x_test)
    fpr, tpr, _ = metrics.roc_curve(y_test_one_hot.ravel(), y_test_one_hot_hat.ravel())
    print ('Micro AUC:\t', metrics.auc(fpr, tpr))
    print ('Micro AUC(System):\t', metrics.roc_auc_score(y_test_one_hot, y_test_one_hot_hat, average='micro'))
    auc = metrics.roc_auc_score(y_test_one_hot, y_test_one_hot_hat, average='macro')
    print ('Macro AUC:\t', auc)

    mpl.rcParams['font.sans-serif'] = u'SimHei'
    mpl.rcParams['axes.unicode_minus'] = False
    plt.figure(figsize=(8, 7), dpi=80, facecolor='w')
    plt.plot(fpr, tpr, 'r-', lw=2, label='AUC=%.4f' % auc)
    plt.legend(loc='lower right')
    plt.xlim((-0.01, 1.02))
    plt.ylim((-0.01, 1.02))
    plt.xticks(np.arange(0, 1.1, 0.1))
    plt.yticks(np.arange(0, 1.1, 0.1))
    plt.xlabel('False Positive Rate', fontsize=14)
    plt.ylabel('True Positive Rate', fontsize=14)
    plt.grid(b=True, ls=':')
    plt.title(u'ROC曲线和AUC', fontsize=18)
    plt.show()