1.LDA贝叶斯模型
????????LDA是基于贝叶斯模型的,涉及到贝叶斯模型离不开“先验分布”,“数据(似然)”和"后验分布"三块。其中:
先验分布 +?数据(似然)=?后验分布
????????先验分布为:100个好人和100个的坏人,即认为好人坏人各占一半,现在如果你被2个好人(数据)帮助了和1个坏人骗了,于是你得到了新的后验分布为:102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布,当你被1个好人(数据)帮助了和3个坏人(数据)骗了后,你又更新了你的后验分布为:103个好人和104个的坏人。依次继续更新下去。
2. 二项分布与Beta分布
????????用数学和概率的方式来表达贝叶斯模型:
? ? ? ? 对于数据(似然),用二项分布来表达:
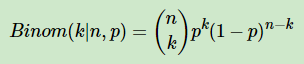
????????其中p我们可以理解为好人的概率,k为好人的个数,n为好人坏人的总数
????????因为我们希望这个先验分布和数据(似然)对应的二项分布集合后,得到的后验分布在后面还可以作为先验分布,也就是说,我们希望先验分布和后验分布的形式应该是一样的,这样的分布一般叫共轭分布。在我们的例子里,我们应该找到和二项分布共轭的分布。
????????和二项分布共轭的分布是Beta分布。Beta分布的表达式为:
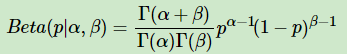
?其中Γ是Gamma函数,满足Γ(x)=(x?1)!
????????Beta分布和二项分布,可以发现两者的密度函数很相似,区别仅仅在前面的归一化的阶乘项。在该情况下,后验分布的推导如下:
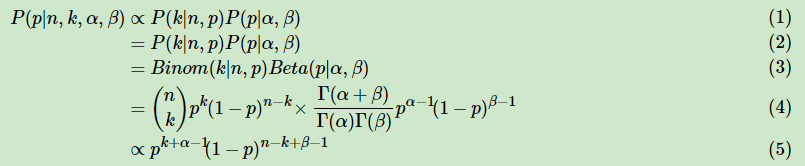
将上面最后的式子归一化以后,得到的后验概率为

可见我们的后验分布的确是Beta分布,同时发现:?
![]()
符合一开始的预想
同时,求出Beta分布的期望:?

?由于上式最右边的乘积对应Beta分布Beta(p|α+1,β)因此有:

这样Beta分布的期望可以表达为:?

?也符合一开始的思路。
3. 多项分布与Dirichlet?分布
????????在文本识别过程中,不止是简单的好人与坏人的区分,同时可能还会有不好不坏的人,那么之前是二维分布,现在成了三维分布,由于二维我们使用了Beta分布和二项分布来表达这个模型,则在三维时,以此类推,我们可以用三维的Beta分布来表达先验后验分布,三项的多项分布来表达数据(似然)。?
????????三项的多项分布好表达,我们假设数据中的第一类有m1个好人,第二类有m2个坏人,第三类为m3=n?m1?m2个不好不坏的人,对应的概率分别为p1,p2,p3=1?p1?p2则对应的多项分布为:?
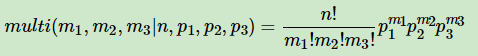
?????????超过二维的Beta分布我们一般称之为狄利克雷(以下称为Dirichlet?)分布。也可以说Beta分布是Dirichlet?分布在二维时的特殊形式。那么三维的Dirichlet分布如下:

????????同样的方法,我们可以写出4维,5维,。。。以及更高维的Dirichlet?分布的概率密度函数。为了简化表达式,我们用向量来表示概率和计数,这样多项分布可以表示为:Dirichlet( |
?),而多项分布可以表示为:multi(
?|
,
?)。
????????一般意义上的K维Dirichlet?分布表达式为:

而多项分布和Dirichlet?分布也满足共轭关系,这样我们可以得到和上一节类似的结论:
![]()
对于Dirichlet?分布的期望,也有和Beta分布类似的性质:
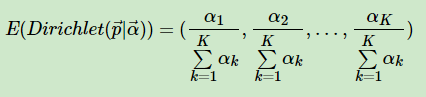
?4. LDA主题模型
??????????我们的问题是这样的,我们有M篇文档,对应第d个文档中有有Nd个词。即输入为如下图:

?我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。在LDA模型中,我们需要先假定一个主题数目K,这样所有的分布就都基于K个主题展开。那么具体LDA模型如下图:

描述流程为:
?从狄利克雷分布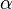
?从主题的多项式分布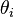
?从狄利克雷分布??中取样生成主题
对应的词语分布
?从词语的多项式分布中采样最终生成词语
?LDA假设文档主题的先验分布是Dirichlet分布,即对于任一文档d, 其主题分布为:
![]()
?其中,α为分布的超参数,是一个K维向量。
????????LDA假设主题中词的先验分布是Dirichlet分布,即对于任一主题k, 其词分布为:
![]()
????????其中,η为分布的超参数,是一个V维向量。V代表词汇表里所有词的个数。?
????????对于数据中任一一篇文档dd中的第n个词,我们可以从主题分布中得到它的主题编号
的分布为:
![]()
而对于该主题编号,得到我们看到的词的概率分布为:??
![]()
????????这个模型里,我们有M个文档主题的Dirichlet分布,而对应的数据有M个主题编号的多项分布,这样(α→→
)就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。?