作者丨小马
编辑丨极市平台
写在前面
由于Transformer对于序列数据进行并行操作,所以序列的位置信息就被忽略了。因此,相对位置编码(Relative position encoding, RPE)是Transformer获取输入序列位置信息的重要方法,RPE在自然语言处理任务中已被广泛使用。
但是,在计算机视觉任务中,相对位置编码的有效性还没有得到很好的研究,甚至还存在争议。因此,作者在本文中先回顾了现有的相对位置编码方法,并分析了它们在视觉Transformer中应用的优缺点。接着,作者提出了新的用于二维图像的相对位置编码方法(iRPE)。iRPE考虑了方向,相对距离,Query的相互作用,以及Self-Attention机制中相对位置embedding。作为一个即插即用的模块,本文提出的iREP是简单并且轻量级的。
实验表明,通过使用iRPE,DeiT和DETR在ImageNet和COCO上,与原始版本相比,分别获得了1.5%(top-1 Acc)和1.3%(mAP)的性能提升(无需任何调参)。
论文和代码地址

论文地址:
https://arxiv.org/abs/2107.14222
代码地址:
https://github.com/microsoft/AutoML/tree/main/iRPE
研究动机
Transformer最近在计算机视觉领域引起了极大的关注,因为它具有强大的性能和捕获Long-range关系的能力。然而,Transformer中的Self-Attention有一个固有的缺陷——它不能捕获输入token的顺序。因此,Transformer在计算的时候就需要显式的引入位置信息。
为Transformer编码位置表示的方法主要有两类。一个是绝对位置编码,另一个是相对位置编码。绝对位置编码 将输入token的绝对位置从1编码到最大序列长度。也就是说,每个位置都有一个单独的编码向量。然后将编码向量与输入token组合,使得模型能够知道每个token的位置信息。相对位置编码 对输入token之间的相对距离进行编码,从而来学习token的相对关系。
这两种编码方式在NLP任务中都被广泛应用,并且证明是非常有效的。但是在CV任务中,他们的有效性还没被很好的探索。因此,在本文中,作者重新思考并改进相对位置编码在视觉Transformer中的使用。
在本文中,作者首先回顾了现有的相对位置编码方法,然后提出了专门用于二维图像的方法iRPE。
方法
方法背景
绝对位置编码
由于Transformer不包含递归和卷积,为了使模型知道序列的顺序,需要注入一些关于token位置的信息。原始Self-Attention采用了绝对位置,并添加绝对位置编码 p = ( p 1 , . . . , p n ) p=(p_1,... ,p_n) p=(p1?,...,pn?)到输入token,用公式表示如下:
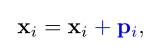
相对位置编码
除了每个输入token的绝对位置之外,一些研究人员还考虑了token之间的相对关系。相对位置编码使得Transformer能够学习token之间的相对位置关系,用公式表示如下:
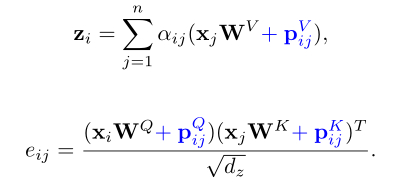
3.2. 回顾相对位置编码
Shaw’s RPE
[1]提出一种Self-Attention的相对位置编码方法。输入token被建模为一个有向全连通图。每条边都代表两个位置之间的相对位置信息。此外,作者认为精确的相对位置信息在一定距离之外是无用的,因此引入了clip函数来减少参数量,公式表示如下:
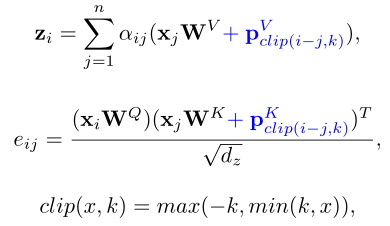
RPE in Transformer-XL
[2]为query引入额外的bias项,并使用正弦公式进行相对位置编码,用公式表示如下:

Huang’s RPE
[3]提出了一种同时考虑query、key和相对位置交互的方法,用公式表示如下:

RPE in SASA
上面的相对位置编码都是针对一维的序列,[4]提出了一种对二维特征进行相对位置编码的方法,用公式表示如下:
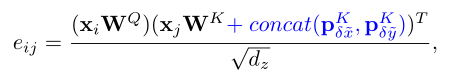
相对位置编码的确定
接下来,作者引入了多种相对位置编码方式,并进行了详细的分析。首先,为了研究编码是否可以独立于输入token,作者引入了两种相对位置模式:Bias模式和Contextual模式 。然后,为了研究方向性的重要性,作者设计了两种无向方法和两种有向方法 。
Bias Mode and Contextual Mode
以前的相对位置编码方法都依赖于输入token,因此,作者就思考了,相对位置的编码信息能否独立于输入token来学习。基于此,作者引入相对位置编码的Bias模式和Contextual模式来研究这个问题。前者独立于输入token,而后者考虑了与query、key或value的交互。无论是哪种模式,相对位置编码都可以用下面的公式表示:
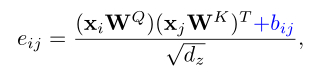
对于Bias模式,编码独立于输入token,可以表示成:

对于Contextual 模式,编码考虑了与输入token之间的交互,可以表示成:

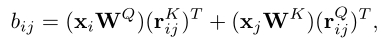
A Piecewise Index Function
由于实际距离到计算距离的关系是多对一的关系,所以首先需要定义一个实际距离到计算距离的映射函数。
先前有工作提出了采用clip函数来进行映射,如下所示:

在这种方法中,相对距离大于 β \beta β的位置分配给相同的编码,因此丢失了远距离相对位置的上下文信息。
在本文中,作者采用了一种分段函数将相对距离映射到相应的编码。这个函数基于一个假设:越近邻的信息越重要,并通过相对距离来分配注意力。函数如下:
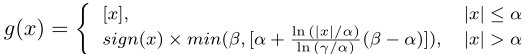
如下图所示,相比于先前的方法,本文提出的方法感知距离更长,并且对不同的距离分布施加了不同程度的注意力。
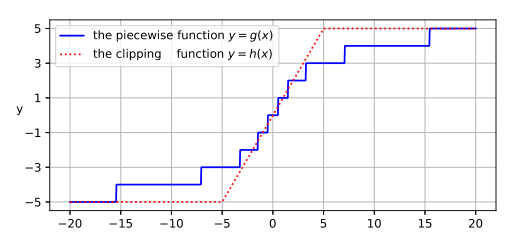
2D Relative Position Calculation
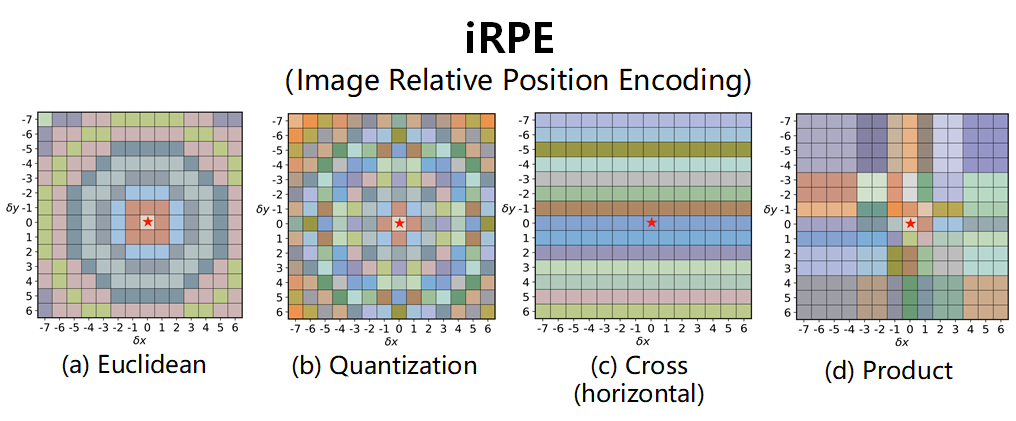
为了衡量二维图像上两个点的相对距离,作者提出了两种无向方法 (Euclidean method,Quantization method)和两种有向方法 (Cross method,Product method),如上图所示。
- Euclidean method
在Euclidean method中,作者采用了欧氏距离来衡量两个点之间的距离,如上图a所示:

- Quantization method
在上述的Euclidean method中,具有不同相对距离的两个距离可能映射到同一距离下标(比如二维相对位置(1,0)和(1,1)都映射到距离下标1中)。因此,作者提出Quantization method,如上图b所示,公式如下所示:
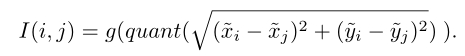
q u a n t ( ? ) quant(·) quant(?)函数可以映射一组实数 0 , 1 , 1.41 , 2 , 2.24 , … {0,1,1.41,2,2.24,…} 0,1,1.41,2,2.24,…到一组整数 0 , 1 , 2 , 3 , 4 , … {0,1,2,3,4,…} 0,1,2,3,4,…。
- Cross method
像素的位置方向对图像理解也很重要,因此作者又提出了有向映射方法。Cross method分别计算水平方向和垂直方向上的编码,然后对它们进行汇总。编码信息如上图c所示,公式如下:
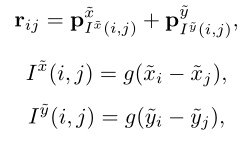
- Product method
如果一个方向上的距离相同(水平或垂直),Cross method将会把不同的相对位置编码到相同的embedding中。因此,作者又提出了Product method,如上图d所示,公式如下所示:

有效实现
对于Contextual模式的相对位置编码,编码信息可以通过下面的方式得到:
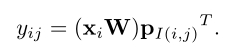
但是这么做的计算复杂度是 O ( n 2 d ) O(n^2d) O(n2d),所以作者在实现的时候就只计算了不同映射位置的位置编码,如下所示:
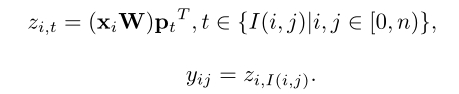
这样做就可以将计算复杂度降低到 O ( n k d ) O(nkd) O(nkd),对于图像分割这种任务,k是远小于n的,就可以大大降低计算量。
4.实验
相关位置编码分析
- Directed-Bias v.s. Undirected-Contextual
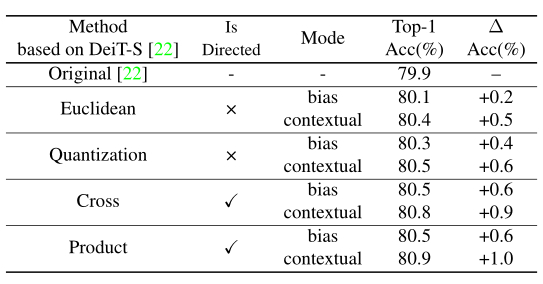
上表的结果表明了:
1)无论使用哪种方法,Contextual模式都比Bias模式具有更好的性能。
2)在视觉Transformer中,有向方法通常比无向方法表现更好。
- Shared v.s. Unshared

对于bias模式,在head上共享编码时,准确度会显著下降。相比之下,在contextual模式中,两种方案之间的性能差距可以忽略不计。
- Piecewise v.s. Clip.

上表比较了clip函数和分段函数的影响,在图像分类任务中,这两个函数之间的性能差距非常小,甚至可以忽略不计。但是从下表中可以看出,在检测任务中,两个函数性能还是有明显差距的。

- Number of buckets

bucket数量影响了模型的参数,上图展示了不同bucket数量下,模型准确率的变化。
- Component-wise analysis
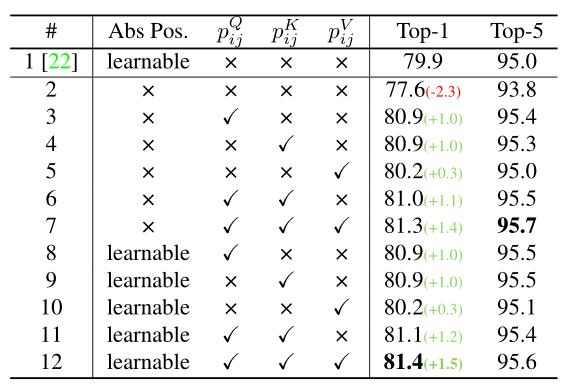
从上表可以看出,相对位置编码和绝对位置编码对DeiT模型的精度都有很大帮助。
- Complexity Analysis

上图表明,本文方法在高效实现的情况下最多需要1%的额外计算成本。
在图像分类任务上的表现
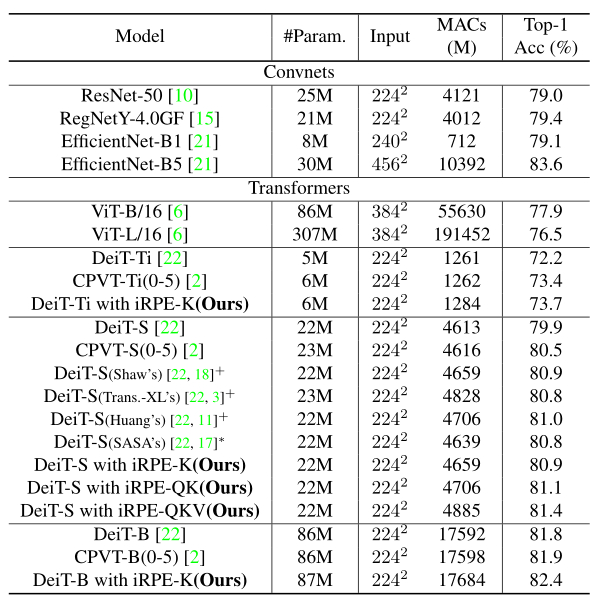
通过仅在key上添加相对位置编码,将DeiT-Ti/DeiT-S/DeiT-B模型分别提升了1.5%/1.0%/0.6%的性能。
在目标检测任务上的表现

在DETR中绝对位置嵌入优于相对位置嵌入,这与分类中的结果相反。作者推测DETR需要绝对位置编码的先验知识来定位目标。
可视化
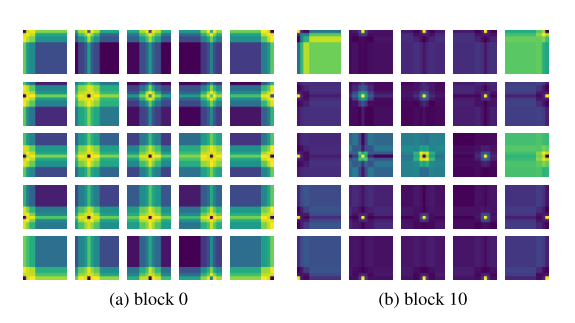
上图展示了Contextual模式下相对位置编码(RPE)的可视化。
5. 总结
本文作者回顾了现有的相对位置编码方法,并提出了四种专门用于视觉Transformer的方法。作者通过实验证明了通过加入相对位置编码,与baseline模型相比,在检测和分类任务上都有比较大的性能提升。此外,作者通过对不同位置编码方式的比较和分析,得出了下面几个结论:
1)相对位置编码可以在不同的head之间参数共享,能够在contextual模式下实现与非共享相当的性能。
2)在图像分类任务中,相对位置编码可以代替绝对位置编码。然而,绝对位置编码对于目标检测任务是必须的,它需要用绝对位置编码来预测目标的位置。
3)相对位置编码应考虑位置方向性,这对于二维图像是非常重要的。
4)相对位置编码迫使浅层的layer更加关注局部的patch。
参考文献
[1]. Peter Shaw, Jakob Uszkoreit, and Ashish Vaswani. Self-attention with relative position representations. ACL, 2018.
[2]. Zihang Dai, Zhilin Yang, Yiming Yang, Jaime G Carbonell,Quoc Le, and Ruslan Salakhutdinov. Transformer-xl: Attentive language models beyond a fixed-length context. In ACL,2019.
[3]. Zhiheng Huang, Davis Liang, Peng Xu, and Bing Xiang. Improve transformer models with better relative position embeddings. In EMNLP, 2020
[4]. Prajit Ramachandran, Niki Parmar, Ashish Vaswani, Irwan Bello, Anselm Levskaya, and Jonathon Shlens. Standalone self-attention in vision models. arXiv preprint arXiv:1906.05909, 2019.