[人工智能]吴恩达《神经网络和深度学习》学习笔记——（一）神经网络的编程基础

第二周：神经网络的编程基础(Basics of Neural Network programming)

前言

简介：本文是笔者在学习该课程的过程中随意记录的一些要点，希望能帮助到大家，欢迎大家留言or私信讨论
参考资料：吴恩达先生的课程材料&黄海广先生整理的深度学习课程笔记(V5.7)

正文

以下是本篇文章正文内容

2.1 二分类(Binary Classification)

eg.一张$64?64$的图维度$n_x=64?64?3=12288$，特征向量为[$n_x$,1]维度列向量

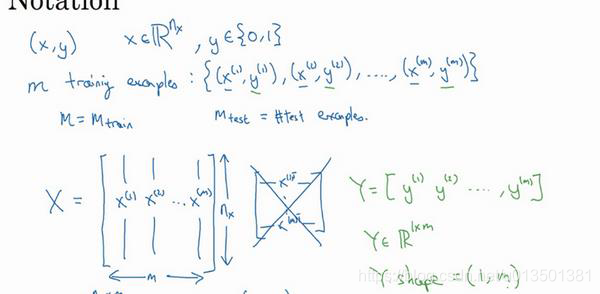
2.2 逻辑回归 (Logistic Regression)

该算法适用于二分类问题

$y=\sigma (w^{T}x+b)$

其中

$y$为y等于1的可能性或者机会

w为特征权重

b为偏差

$\sigma$图像如下所示，$z=w^{T}x+b$，$\sigma (z)=\frac{1}{1+e^{?z}}$，其中z为实数

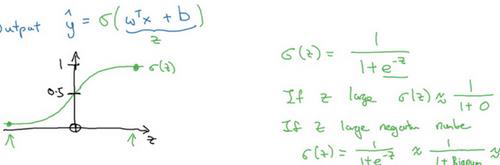
2.3 逻辑回归的代价函数（ Logistic Regression Cost Function）

Why need 代价函数

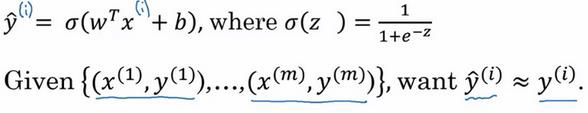
? 对于每个训练样本，我们使用这些带有圆括号的上标来区分索引和样本，训练样本 𝑖所对应的预测值是$y^{(i)}$,是用训练样本的$w^T{x}^{(i)}+b$然后通过 sigmoid函数来得到。

? 上标 (𝑖)来指明数据表示 𝑥或者 𝑦或者 𝑧或者其他数据的第 𝑖个训练样本。

损失函数

? Loss function：$L(y,y)$

? 我们通过这个𝐿称为的损失函数，来衡量预测输出值和实际值有多接近。

? 我们在逻辑回归中用到的损失函数是：$L(y,y)=?ylog(y)?(1?y)log(1?y)$

代价函数

? $J(w,b)=\frac{1}{m}{\sum }_{i=1}^{m}L(y^{(i)},y^{(i)})$

? 损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型时候，我们需要找到合适的 𝑤和 𝑏，来让代价函数 𝐽 的总代价降到最低。

? 逻辑回归可以看做是一个非常小的神经网络

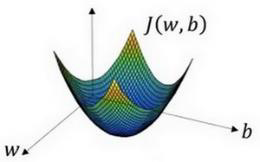
2.4 梯度下降法（ Gradient Descent）

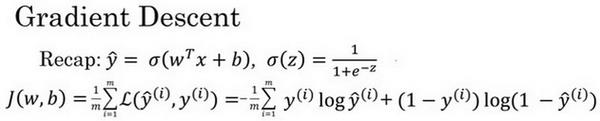
? 梯度下降法的形象化说明

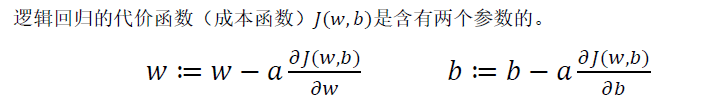
2.5 导数（ Derivatives）

2.6 更多的导数例子（ More Derivative Examples）

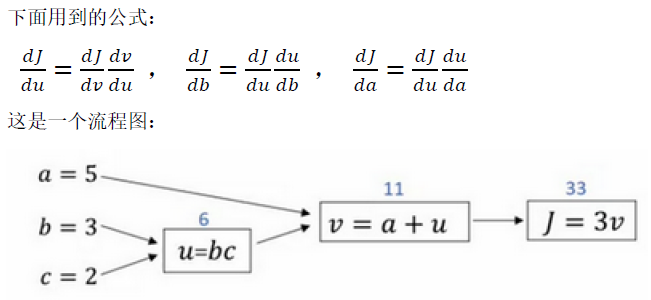
2.7 计算图（ Computation Graph）

? 计算图组织计算的形式是用蓝色箭头从左到右的计算，反向红色箭头 (也就是从右到左 )的导数计算

2.8 使用计算图求导数 （Derivatives with a Computation Graph）

2.9 逻辑回归中的梯度下降（ Logistic Regression Gradient Descent）

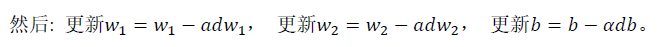
2.10 m 个样本的梯度下降 (Gradient Descent on m Examples)

2.11 向量化 (Vectorization)

2.12 向量化的更多例子（ More Examples of Vectorization）

2.13 向量化逻辑回归 (Vectorizing Logistic Regression)

$Z=[z^{(1)},z^{(2)},...,z^{(n)}]$其中$z=w^{T}x+b$

2.14 向量化 logistic 回归的梯度输出（ Vectorizing Logistic Regression’s Gradient）

2.15 Python 中的广播（ Broadcasting in Python）

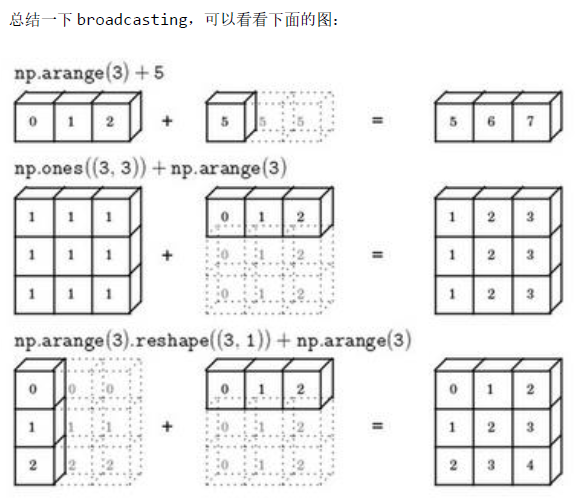
2.16 关于 python _ numpy 向量的说明（ A note on python or numpy vectors）参考视频

注意要养成加断言的好习惯

2.17 Jupyter/iPython Notebooks快速入门（ Quick tour of Jupyter/iPython Notebooks）

2.18 （选修 logistic 损失函数的解释（ Explanation of logistic regression cost function）

*HomeWork

总结

以上就是神经网络的编程基础(第二周)的部分学习笔记，本文仅仅简单记录了在学习过程中个人认为比较重要的要点。