[人工智能]Neuroprosthesis for Decoding Speech in a Paralyzed Person with Anarthria-Language modeling

摘要

在获取单词后，需要对获得的单词词序进行预测。文章通过语言建模，在给定序列中前一个单词的情况下生成下一个单词的概率，以在受试者试图说出这些单词时解码完整的句子。

模型拟合和词序概率

为了适配在句子解码期间使用的语言模型 ，首先先使用Amazon Mechanical Turk 任务众包训练语料库。
该语料库包含 3415 个句子，仅由 50 个单词集中的单词组成。 为了防止语言模型在最常见的句子上过度拟合，在根据这些响应为语言模型创建训练语料库时，语料库最多只包含每个唯一句子的 15 个实例。

n-gram模型

N-Gram是一种基于统计语言模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为N的滑动窗口操作，形成了长度是N的字节片段序列。
每一个字节片段称为gram，对所有gram的出现频度进行统计，并且按照事先设定好的阈值进行过滤，形成关键gram列表，也就是这个文本的向量特征空间，列表中的每一种gram就是一个特征向量维度。
该模型基于这样一种假设，第N个词的出现只与前面N-1个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的Bi-Gram和三元的Tri-Gram。

N-gram模型的一个常见应用
搜索引擎（Google或者Baidu）、或者输入法的猜想或者提示。在用谷歌时，输入一个或几个词，搜索框通常会以下拉菜单的形式给出几个像下图一样的备选，这些备选其实是在猜想想要搜索的那个词串。

再者，当用输入法输入一个汉字的时候，输入法通常可以联系出一个完整的词，例如输入一个“刘”字，通常输入法会提示是否要输入的是“刘备”。这其实是以N-Gram模型为基础来实现的。比如下图：

接下来，从训练语料库的每个句子中提取所有 n-gram，其中 n ∈ {1, 2, 3, 4, 5}。 这里，n-gram 是一个长度为 n 个单词的单词序列 。 例如，从句子“我希望我的家人来了”中提取的 n-gram（表示为元组）。
这种方法是：

1. (I)
2. (Hope)
3. (My)
4. (Family)
5. (Is)
6. (Coming)
7. (I, Hope)
8. (Hope, My)
9. (My, Family)
10. (Family, Is)
11. (Is, Coming)
12. (I, Hope, My)
13. (Hope, My, Family)
14. (My, Family, Is)
15. (Family, Is, Coming)
16. (I, Hope, My, Family)
17. (Hope, My, Family, Is)
18. (My, Family, Is, Coming)
19. (I, Hope, My, Family, Is)
20. (Hope, My, Family, Is, Coming)

我们使用以这种方式从训练语料库中的所有句子中提取的 n-gram 来拟合带有 nltk Python 包的 5 阶内插 Kneser-Ney n-gram 语言模型 [28, 29]。 该模型使用了 0.1 的折扣因子，这是 nltk 中指定的默认值。 这种语言模型架构的细节，以及它在各种语料库建模任务上优于更简单的 n-gram 架构的能力的特征，可以在现有文献 [27, 28] 中找到。
使用训练语料库中特定词序列的出现频率（由提取的 n-gram 指定），语言模型被训练以产生给定该词上下文的任何词出现的条件概率，即(n ? 1) 个或更少的单词。 这些概率可以表示为 p (wi | ci,n)，其中 wi是某个词序列中位置 i 的词，ci,n 是该词的上下文 32 假设它是 n-gram 的一部分（这个 n-gram 是一个包含 n 个词的词序列，wi 作为最后一个词 该序列），并且 n ∈ {1, 2, 3, 4, 5}。 词 wi 的上下文定义为以下元组：

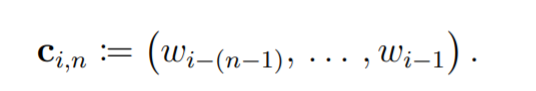
当 n = 1 时，上下文是 ()，一个空元组。 当 n = 2 时，单词 wi 的上下文是 (wi-1)，一个包含 wi 之前的单词的单元素元组。 使用这项工作中使用的语言模型，这种模式一直持续到 n = 5，其中单词 wi 的上下文是 (wi?4, wi?3, wi?2, wi?1)，一个包含四个单词的元组 在 wi 之前的序列中（按顺序）。 要求每个 wi ∈ W，其中 W 是 50 个词的集合。 此要求也适用于上下文 ci,n 中包含的单词。

句子独立

在句子任务期间，每个句子都独立于任务块中的另一个句子进行解码。 我们在语言模型推理过程中使用的上下文 ci,n 只能包含前面的单词，但也与 wi 位于同一个句子中（上下文从不跨越两个或多个句子）。 我们在推理过程中使用的上下文中的值 i 和 n 之间的关系可以表示为：

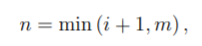
其中 m 是模型的阶数（对于该模型，m = 5），i = 0 指定句子中初始词的索引。 将 n 的这个定义代入方程 S12 中指定的 ci,n 的定义，得到其中 m 是模型的阶数（对于该模型，m = 5），i = 0 指定句子中初始词的索引。 将 n 的这个定义代入方程 S12 中指定的 ci,n 的定义，得到：

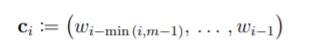
其中 ci 是句子试验中单词 wi 的上下文。 这种代换将语言模型得到的词概率的形式简化为p(wi|ci)。

初始词概率

由于在此任务中句子总是独立解码，因此在对句子中的初始词 w0 进行推理时，空元组仅用作上下文。 我们没有使用语言模型在推理过程中产生的 p (w0 | c0) 值，而是使用直接来自语料库的字数和两种不同类型的平滑。 首先，我们计算了以下概率：

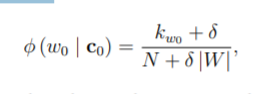
其中 kw0 是单词 w0 在训练语料库中作为句子中初始单词出现的次数，N 是训练语料库中的句子总数，δ 是加性平滑因子。 在这里，加性平滑因子是在归一化之前添加到所有计数 kw0 的值，它平滑（减少了概率分布的方差）[27]。 在这项工作中，N = 3415，δ = 3，和 |W| = 5。

然后我们平滑了这些 φ (w0 | c0) 值，以进一步控制初始单词概率的概率分布有多平坦。 这可以解释为控制语言模型对初始单词概率预测的“信心”程度（概率分布越平坦表示信心越低）。 我们使用超参数来控制这种平滑的程度，允许超参数优化过程确定在测试期间优化的平滑程度（有关超参数优化过程的描述，请参见部分 S7 和表 S1）。 我们使用以下等式来执行此平滑：

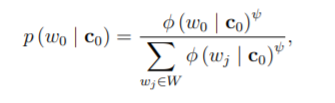
其中 ψ 是初始词平滑超参数值。 当 ψ > 1 时，初始词概率的方差增加，使它们不太平滑。 当 ψ < 1 时，初始词概率的方差减小，使它们更平滑。 当 ψ = 1 时，p (w0 | c0) = φ (w0 | c0)。 请注意，方程 S16 中的分母用于重新归一化平滑后的概率，使它们的总和为 1。

其中 ψ 是初始词平滑超参数值。当 ψ > 1 时，初始词概率的方差增加，使它们不太平滑。当 ψ < 1 时，初始词概率的方差减小，使它们更平滑。当 ψ = 1 时，p (w0 | c0) = φ (w0 | c0)。请注意，方程 S16 中的分母用于重新归一化平滑后的概率，使它们的总和为 1。
本工作中使用的 Viterbi 解码模型包含一个语言模型缩放因子 (LMSF)，这是一个单独的超参数，可在期间重新缩放 p (wi | ci) 值
句子解码方法（有关更多详细信息，请参阅第 S11 节）。这个超参数对所有语言模型概率的影响类似于 ψ 对初始词概率的影响。这应该鼓励超参数
优化程序以找到一个 LMSF 值，该值可以最佳地缩放语言模型概率，以及一个 ψ 值，该值可以相对于随后应用于它们的缩放来优化平滑初始单词概率。

实时执行

为了确保实时解码期间的快速推理，我们使用语言模型预先计算了 p (wi | ci) 值，并为 wi 和 ci 的每个可能组合平滑超参数值，然后将这些值存储在 hdf5 文件中 [30] . 该文件在实时解码期间用作查找表； 这些值存储在文件内的多维数组中，并且在使用 h5py Python 包 [31] 的实时解码期间实现了对表的高效查找查询。 在这种需要更大词汇量的解码方法的未来迭代中，可能更适合使用更复杂的语言模型，该语言模型的计算效率也足以进行实时推理，例如 kenlm 语言模型 [32]。