行人重识别ReID
算法的提高主要体现在损失函数的设计上,损失函数会对整个网络的优化有着导向性的作用。
ReID任务在大多数情况下都是多任务学习,主流是分为两个任务,一个是构建id loss,通过分类损失,来学习对应不同id的损失,另一种是triple loss为主的通过特征向量直接构建的损失,学习类内的相似性和类内的区分性,让不同的特征向量直接的区分度更高,让相同的特征向量更加趋同。
在ReID中常见的loss有Identity Loss、Verification Loss、Triplet loss
Base line Softmax loss
各种延伸的算法 Triplet loss, center loss
###########
id loss 的目的是对特定领域的信息进行建模,以便在每个模式中区分不同的人。
contast loss弥补了两种异质模式之间的差距,增强了学习表征的模式差异。
1、Cross-entropy loss
交叉熵是常见的分类损失,用来描述了两个概率分布之间的距离,当交叉熵越小说明二者之间越接近。
1)普通交叉熵损失
y’是经过激活函数的输出,所以在0-1之间。可见普通的交叉熵对于正样本而言,输出概率越大损失越小。对于负样本而言,输出概率越小则损失越小。
2)label smooth
当然在ReID的过程中还是存在很多的负样本,类别越多负样本的数量越大,为了做好负样本的损失构建而不是忽略负样本,可以在交叉熵中引入label smooth的操作,与传统交叉熵不同,不强制将类别考虑为0/1,而是有一定概率计算,具体公式如下:
目的是由于一些id的图片量太少了,防止过度拟合训练集。这个策略也是提高了模型的泛化能力的,防止对训练集中的类别过度拟合,根据查阅资料这个也是一个好的策略。
(1)对比损失(Contrastive loss)
对比损失用于训练孪生网络(Siamese network)。孪生网络的输入为一对(两张)图片,其实就是损失函数的计算,还是一个网络。标签相同y=1,不同为0,对比损失函数写作:
(2)三元组损失(Triplet loss)
三元组损失是一种被广泛应用的度量学习损失,之后的大量度量学习方法也是基于三元组损失演变而来。顾名思义,三元组损失需要三张输入图片。和对比损失不同,一个输入的三元组(Triplet)包括一对正样本对和一对负样本对。三张图片分别命名为固定图片(Anchor) a ,正样本图片(Positive)p和负样本图片(Negative) n 。图片 a 和图片 p 为一对正样本对,图片 a 和图片 n 为一对负样本对。则三元组损失表示为:
Triplet loss属于Metric Learning, 相比起softmax, 它可以方便地训练大规模数据集,不受显存的限制。缺点是过于关注局部,导致难以训练且收敛时间长
这里提一下Metric Learning的概念,它是根据不同的任务来自主学习出针对某个特定任务的度量距离函数。通过计算两张图片之间的相似度,使得输入图片被归入到相似度大的图片类别中去。通常的目标是使同类样本之间的距离尽可能缩小,不同类样本之间的距离尽可能放大。
后来有改进版认为原版的Triplet loss只考虑正负样本对之间的相对距离,而并没有考虑正样本对之间的绝对距离,为此提出改进三元组损失(Improved triplet loss):
保证网络不仅能够在特征空间把正负样本推开,也能保证正样本对之间的距离很近。
1、 Softmax loss
这就是softmax loss函数,xxxxxxxxx表示全连接层的输出。在计算Loss下降的过程中,我们让{W^T_{j}x_i+b_{j}} 的比重变大,从而使得log() 括号内的数更变大来更接近1,就会 log(1) = 0,整个loss就会下降。
这种方式只考虑了能否正确分类,却没有考虑类间距离。
softmax是最常见的人脸识别函数,其原理是去掉最后的分类层,作为解特征网络导出特征向量用于人脸识别。softmax训练的时候收敛得很快,但是精确度一般达到0.9左右就不会再上升了,一方面是作为分类网络,softmax不能像metric learning一样显式的优化类间和类内距离,所以性能不会特别好,另外,人脸识别的关键在于得到泛化能力强的feature,与分类能力并不是完全等价的。
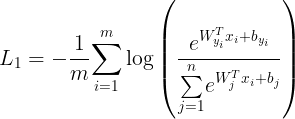
2、center loss
可以看到,在separable features中,类内距离有的时候甚至是比内间距离要大的,这也是上问题到softmax效果不好的原因之一,它具备分类能力但是不具备metric learning的特性,没法压缩同一类别。在这个基础上,center loss被提出来,用于压缩同一类别。center loss的核心是,为每一个类别提供一个类别中心,最小化每个样本与该中心的距离:
https://blog.csdn.net/u012505617/article/details/89355690