一、什么是Seq2Seq？

Seq2Seq(Sequence to Sequence), 就是一种能够根据给定的序列，通过特定的方法生成另一个序列的方法。它被提出于2014年，最早由两篇文章独立地阐述了它主要思想，分别是Google Brain团队的《Sequence to Sequence Learning with Neural Networks》和Yoshua Bengio团队的《Learning Phrase Representation using RNN Encoder-Decoder for Statistical Machine Translation》。这两篇文章不谋而合地提出了相似的解决思路，Seq2Seq由此产生。Seq2Seq是一个Encoder-Decoder结构，其中Encoder为一个RNN结构，Decoder也为一个RNN结构，当然这里的RNN结构可以替换成为LSTM或者GRU等。我们以机器翻译的例子进行讲解，如下图，我们希望将汉语小明吃苹果翻译成为英文。首先是对汉语进行分词处理得到小明，吃，苹果三个词语，而我们希望输出的是xiao ming eats apples.具体的流程见下图：
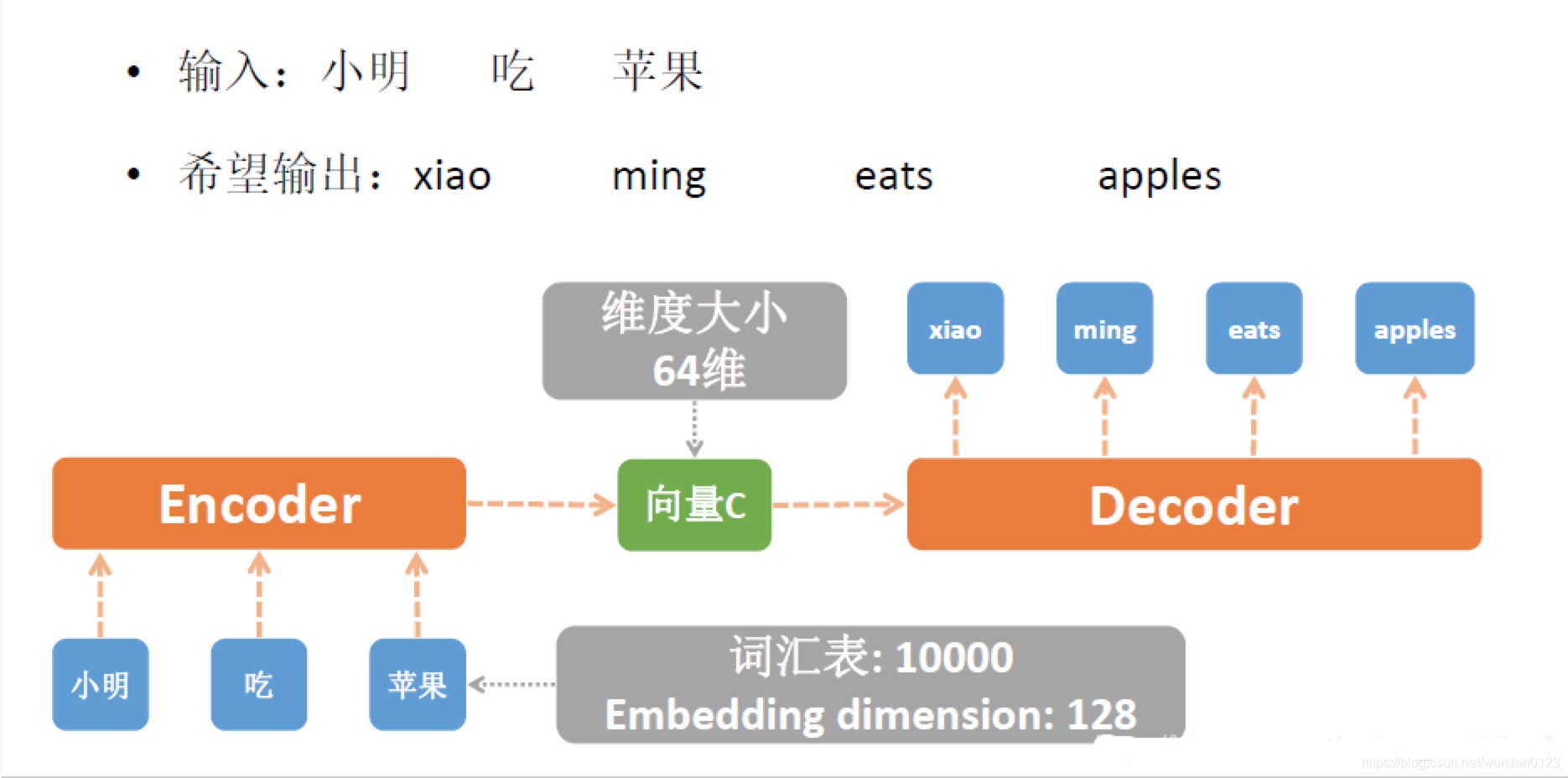
在这里插入图片描述

二、Seq2Seq的应用场景

Seq2Seq的应用随着计算机技术、人工智能技术、算法研究等方面的发展以及社会发展的需求，它在许多领域产生了一些运用。目前，它主要的应用场景有

机器翻译
对话机器人
文本摘要自动生成
图片描述自动生成
机器写诗歌
代码补全、生成 commit message
故事风格改写

当然seq2seq的应用不仅局限于此，工业界有更多的应用等着我们去挖掘。

三、Seq2Seq原理解析

Seq2Seq模型是基于输入序列，预测未知输出序列的模型。它有两个部分组成，对输入序列的Encoder编码阶段和生成输出序列的Decoder解码阶段。
我们使用 $x=[x_1,x_2,\cdots,x_n]$ 代表输入的语句， $y=[y_1, y_2, \cdots, y_n]$ 代表输出的语句， $y_t$ 代表当前输出词。在理解seq2seq的过程中，我们要牢记我们的目标是：
$p(y|x)=g(h_{<t>},y_{t},c)=\prod_{t=1}^{n_y}p(y_t|y_{1},y_{2},\cdots,y_{t-1},x)\quad\quad(1)$
即输出的 $y_t$ 不仅依赖之前的输出 $[y_1, y_2, \cdots, y_{t?1}]$ ，还依赖输入语句 $x$ ，模型再怎么变化都是在公式(1)的约束之下。

seq2seq最初模型

最早由bengio等人发表在computer science上的论文：Learning Phrase Representations using RNN Encoder–Decoder
for Statistical Machine Translation。
对于RNN来说， $x=[x_1,x_2,\cdots,x_t]$ 代表输入，在每个时间步 $t$ ，RNN的隐藏状态 $h_t$ 由公式(1)更新:
$h_t=f(h_{t?1},x_t)\quad\quad(2)$
其中， $f$ 代表一个非线性函数。这时 $h_t$ 就是一个rnn_size的隐含状态。然后需要通过一个矩阵 $W$ 将其转成一个symbol_size的输出，并通过softmax函数将其转化为概率，然后筛选出概率最大的symbol为输出symbol。
$p(x_{t,j}=1|x_{t-1},\cdots,x_{1}=\dfrac{e^{w_jh_{<t>}}}{\sum_{j'=1}^{K}e^{w_{j'}h_{<t>}}}\quad\quad(3)$
以上是rnn的基本原理，接下来介绍论文中的seq2seq模型：
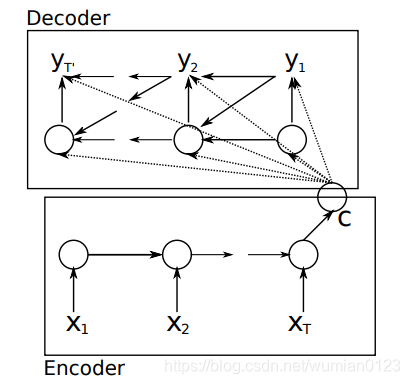
在这里插入图片描述
上图中可以看出，Encoder使用RNN编码后形成语义向量 $C$ ，再将 $C$ 作为输出序列模型Decoder的输入。解码过程中每一个时间点 $t$ 的输入是上一个时刻隐层状态 $h_{t-1}$ 和中间语义向量 $C$ 和上一个时刻的预测输出 $y_{t-1}$ ，之后将每个时刻的 $y_t$ 相乘得到整个序列出现的概率，其中 $f$ 是非线性的激活函数。
$h_{<t>}=f(h_{<t-1>},y_{t-1},c)$
由此我们的到了decoder的隐藏状态，那么最后的输出 $y_t$ 从图中也可以看得出来由三部分得到， $h_{t}$ ， $y_{t-1}$ 和 $C$ ，即：
$P(y_t|y_{t-1},y_{t-2},\cdots,y_1,c)=g(h_{<t>},y_{t},c)$
最后Seq2Seq两个部分(Encoder和Decoder)联合训练的目标函数是最大化条件似然函数。其中 $θ$ 为模型的参数， $N$ 为训练集的样本个数。
$\max_{\theta}\dfrac{1}{N}\sum_{n=1}^{N}logp_{\theta}(y_{n}|x_{n})$

seq2seq的改进模型

改进模型介绍2014年发表的论文：Sequence to Sequence Learning with Neural Networks。模型图：
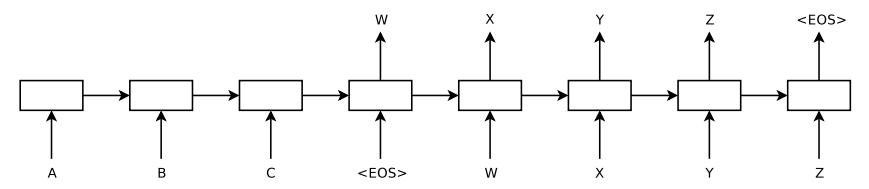
在这里插入图片描述
可以看到，该模型和第一个模型主要的区别在于从输入到输出有一条完整的流：ABC为encoder的输入，WXYZ为decoder的输入。将encoder最后得到的隐藏层的状态 $h_t$ 输入到decoder的第一个cell里，就不用像第一个模型一样，而一个decoder的cell都需要 $h_t$ ，因此从整体上看，从输入到输出像是一条“线性的数据流”。本文的论文也提出来，ABC翻译为XYZ，将encoder的input变为“CBA”效果更好。即A和X的距离更近了，更有利于seq2seq模型的交流。
具体来说，encoder的过程如下图。这和我们之前的encoder都一样。
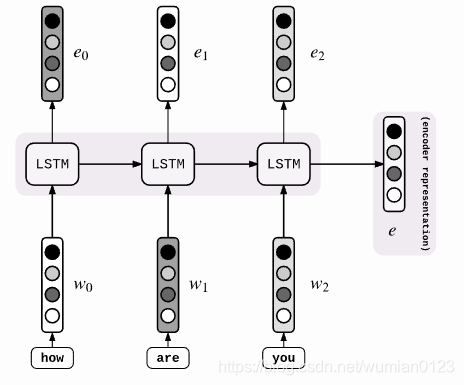
在这里插入图片描述
不同的是decoder的阶段：

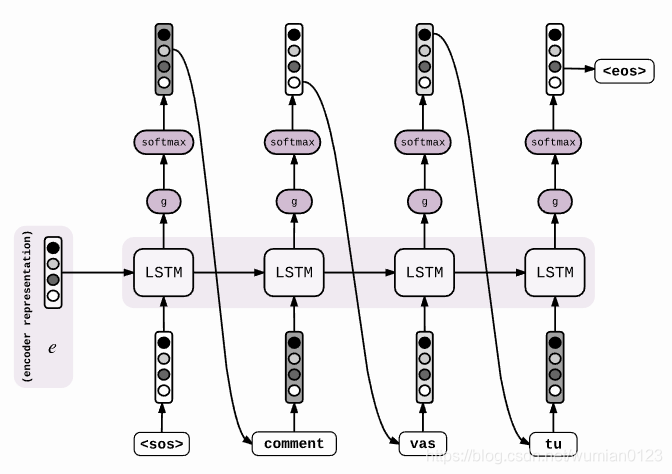
得到了encoder represention，即encoder的最后一个时间步长的隐层 $h_t$ 以后，输入到decoder的第一个cell里，然后通过一个激活函数和softmax层，得到候选的symbols，筛选出概率最大的symbol，然后作为下一个时间步长的输入，传到cell中。这样，我们就得到了我们的目标(1)。