[人工智能]Neural Encoder-Decoder论文笔记-2020-BMC Genomics

摘要

背景:新一代测序(NGS)和色谱分析的技术进步。液相色谱质谱法(LC-MS)]已经使鉴定数千种微生物和代谢物物种并测量它们的相对丰度成为可能。在本文中，我们提出了一个稀疏神经编码器-解码器网络来从微生物丰度预测代谢产物丰度。
结果:使用来自炎症性肠病(IBD)患者队列的配对数据，我们表明，我们的神经编码器-解码器模型在准确性、稀疏性和稳定性方面优于线性单变量和多变量方法。重要的是，我们证明了我们的神经编码器-解码器模型不仅仅是一个为了最大化预测准确性而设计的黑盒子。相反，该网络的隐藏层(即仅由稀疏加权的微生物计数组成的潜在空间)实际上捕获了本身具有临床意义的关键微生物-代谢物关系。虽然这个隐藏层是在不知道患者诊断的情况下学习的，但我们表明，学习的潜在特征是在一种预测IBD和治疗状态高准确性的方式构建的。
结论:通过施加非负权约束，网络成为一个有向图，其中每个下游节点都可以解释为上游节点的相加组合。在这里，中间层包含不同的微生物代谢物轴，将关键的微生物生物标志物与代谢物生物标志物联系起来。通过使用成分数据分析方法对微生物组和代谢组数据进行预处理，我们确保我们提出的多组学工作流将适用于任何一对组学数据。据我们所知，这项工作是神经编码器-解码器在多组生物数据的可解释集成方面的首次应用。
关键词:代谢组学，多组学，机器学习，深度学习，可解释性

背景

??人类肠道是一个宿主细胞和外来生物共存、合作和竞争的复杂生态系统。在这个生态系统中悬浮着一种营养代谢物的环境，它们就像货币一样，被生活在环境中的生物交换和转换。新一代测序(NGS)和色谱分析技术的进步液相色谱质谱法(LC-MS)]已经使鉴定数千种微生物和代谢物物种并测量它们的相对丰度成为可能。通过将NGS和LC-MS应用于粪便样本，人们对肠道细菌产生、消耗和诱导代谢环境的复杂生态系统获得了两种互补的“视图”。这些数据模式都促进了我们对炎性肠病[1]等难以捉摸的肠道疾病的理解，而且越来越多的数据同时被收集[2-4]。
??炎症性肠病(IBD)一度罕见，现已成为发达国家的主要健康负担，其发病率自第二次世界大战以来稳步上升[5]。IBD是两种截然不同的临床症状的总称，克罗恩病(CD)和溃疡性结肠炎(UC)，两者的特征都是由遗传和环境因素引起的胃肠道(GI)慢性免疫紊乱[6，7]。CD在胃肠道的任何部分都表现为片状的跨壁(深)炎症，而UC的特点是弥漫的粘膜(浅)炎症，从直肠延伸到结肠[8]。虽然IBD的炎症没有感染性来源，但CD和UC患者的肠道微生物群不规则，细菌多样性较少，健康细菌减少，不健康细菌过多[5，9，10]。这些变化部分归因于对良性共生生物体的异常免疫反应[5]。微生物群的不规则性，称为生物失调，也与微生物功能[11]和新陈代谢谱[12]的同步变化有关，两者共同会扰乱正常的肠道生理。例如，Marchesi等人。在IBD粪便样本中发现较低水平的短链脂肪酸[13]，这可能与肠道细菌代谢碳水化合物的方式改变有关[1]。
??Franzosa等人研究了164名IBD患者和56名健康对照者的配对微生物和代谢谱，产生了最大的可公开使用的多组学数据集[14]。在他们的多组学分析中，作者报告说，在所有可能的成对关联中，只有6%具有统计学意义，并得出结论，代谢物与微生物组“倾向于不机械地关联”[14]。然而，多组学数据集成可以通过几种方式进行，从简单到复杂不等。我们将这些方法分为四个层次。第一种方法也是最简单的，使用迭代的单变量-单变量回归，例如，测量单个细菌和单个代谢物之间的Pearson相关性(如Franzosa等人[14]所做的)。这个简单的方法在几个微生物组特定的软件工具[15]中实现。虽然两两关联很容易解释，但它们缺乏模拟细菌(或代谢物)共存的附加效应的能力。第二种方法使用迭代的单变量多变量回归，例如，测量单个细菌作为所有代谢物的功能(反之亦然)。这种方法仍然很容易解释，并已用于从DNA突变[16]和微生物组[2]的代谢物变量推断基因表达。第三种方法使用单一的多变量-多变量回归，如典型相关(CanCor)分析 。CanCor是一个强大的工具，可以找到与代谢物组合最相关的微生物组合。这项技术已经被应用于研究IBD患者的挥发性呼吸代谢产物与肠道菌群的关系[17]，但其广泛应用受到高维[1]的限制(至少没有正则化[18])。
??为了进一步深入建模，我们探索了第四层，它利用多层神经网络对单个多变量-多变量回归进行建模。这些网络的隐藏层就像交换机一样，通过一组中间节点连接输入层和输出层，这些中间节点可以学习层之间的复杂(非线性)模式。在生物学中，深度神经网络已被用于许多应用，包括预测1000个标志性基因中的20000个基因的表达[19]。虽然有用，但这些网络的隐藏层并没有将模型与真实的生物过程联系起来的自然含义。为了解决这一局限，许多神经网络遵循编码器-解码器模式，其中网络具有沙漏形状，其特征是具有压缩输入输出关系的狭窄中间层。这一层被规则化为低维，使其只有足够的信息空间来描述输入输出变换。因此，所有其他信息都会被过滤掉。这一层将网络分为两个专门的部分：编码器和解码器。人们可以把一个通用的编解码器网络想象成一个神经“信号翻译器”，旨在通过中间表示Z将一个数据集X转换成另一个数据集Y。
??编码器-解码器网络已经在计算机视觉中以完全卷积模型的形式进行了研究[20]，其中图像被编码成紧凑的表示，然后被解码成所需的特征映射。在生物医学成像中，U-net[21]已成功地分割了细胞图像，编码器和解码器形成了U形的两个相互作用的轴。在生物学中，自动编码器(一种输入和输出完全相同的特殊类型的编码器-解码器体系结构)已被用于将酵母、假单胞菌和癌细胞聚集在一起，其中隐藏的一层被认为提供了对数据具有生物学意义的抽象[22]。然而，将一个数据域转换到另一个数据域的通用编解码器显然还没有用于多组学数据集成。在这种广义形式中，编解码器可以像CanCor一样，通过潜在空间从多个输入预测多个输出。与CanCor不同，编解码器了解特征之间的深度非线性关系。
??使用编解码器架构，我们试图找到一个好的模型，它可以在多组学数据中提供简单、描述性和可验证的模式。在本文中，我们介绍了我们高度可解释的神经编解码器，旨在了解肠道微生物群与其周围代谢物之间的非线性和协同关系。在这样做的过程中，我们证明了(a)神经网络在微生物代谢组预测中优于线性模型，并且(b)因为加上网络稀疏和非负权重约束，提高了编码器-解码器模型的准确性、稳定性和可解释性。重要的是，我们证明了我们的神经编解码器模型不是一个简单的黑匣子，它的设计目的是最大限度地提高预测精度。相反，网络的隐层(即潜在空间，仅由稀疏加权的微生物计数组成)实际上捕获了本身具有临床意义的关键微生物-代谢物关系。虽然这个隐藏层是在不知道患者的诊断的情况下学习的，但我们证明了学习的潜在特征是以一种高精度预测IBD和治疗状态的方式构建的。综上所述，我们的工作表明，配对的多组学数据可以使用神经网络进行集成，其隐层在没有任何监督的情况下提取输入数据的临床有意义的表示。通过使用标准的合成方法对数据进行预处理，我们确保我们的编码器-解码器工作流程将适用于任何一对组学数据。

结论

??炎症性肠病(IBD)是发达国家的主要健康负担。虽然IBD不是传染性的，但克罗恩病(CD)和溃疡性结肠炎(UC)的患者表现出肠道微生物群异常和肠道代谢组改变。在本文，我们提出了一个神经编码器-解码器模型来学习一组加权连接，这些连接可以仅使用微生物丰度来预测代谢物丰度。我们发现这种神经网络在微生物代谢组预测上优于线性模型，稀疏化加上非负权重约束，进一步提高了编解码器模型的准确性、稳定性和可解释性。重要的是，神经编解码器模型不只是一个旨在最大限度提高预测精度的黑匣子。相反，模型的隐藏层可以帮助可视化微生物和代谢物之间的预测关系。此外，学习的潜在特征空间(即，隐藏节点本身)似乎以临床一致的方式构建数据：该潜在空间与IBD诊断和药物使用相关联，并对其进行预测。我们的发现表明，微生物-代谢物轴本身，而不仅仅是微生物和代谢物本身，是IBD特异性生物标记物的标志。据我们所知，这项工作是首次应用神经编解码器对多组学生物数据进行可解释集成。

方法

Data acquisition and processing

??我们从Franzosa等人的补充中获得成对的微生物组和代谢组数据作为原始比例[14]。为了降低数据的维度，我们删除了超过50%的测量值为零的特征。我们通过zComposations中的cmultRepl零替换函数，用非常小的数字来替换剩余的零，这是一个显式建模NGS和LC-MS数据的相对性质的归因工具[23]。接下来，我们通过两条管道之一来处理数据：“完整”或“概括”（ “Complete” or “Summarized” ）。
??在“Complete”管道中，我们直接对菌种水平和代谢产物聚类水平的丰度进行了中心对数比例(CLR)变换。CLR是成分数据分析的基石[24-27]：

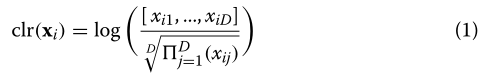
其中，xi是一个细菌或代谢物丰度的样本向量。除了将数据转换为实数外，clr还便于机器学习应用，因为“归一化因子”应用于每个样本，与其他所有样本无关，从而保持测试集的独立性。
??在“Summarized”管道中，我们通过对各自的属成员进行求和，将细菌物种级的丰度聚合到属级的丰度。我们还通过对各个类成员进行求和，将代谢物聚类水平的丰度聚集到类水平。我们从综合分类信息系统(ITIS)(通过R包taxize[28])中检索到种-属（species-to-genus)转换表，从Franzosa等人的[14]补充中检索到代谢产物-类(metabolite-to-class)转换表。不属于任何属或纲的特征被剔除。表1描述了处理前后数据的维度。

Our motivation: predicting metabolites from microbes

??如果我们能找到一种方法从其中一种数据（微生物）来预测另一种数据（代谢物），那么这两个数据模态之间的关系的本质就可以明确地表示出来。理想的模型不仅能识别数据对之间的相关性，还能揭示它们相互影响的机制。这些复杂的过程可以从回归模型的角度来考虑，回归模型可以根据细菌的丰度来预测代谢物的丰度。
??我们将预测问题表示为利用参数集θ来寻找参数函数f，该参数函数将(经clr变换的)微生物丰度X作为输入，以估计真实(经clr变换)观测Y的预测(经clr变换)代谢物丰度?Y：


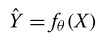
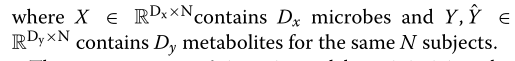
??通过最小化预测和真实观测值误差来估计参数集θ，例如可使用均方误差（MSE):

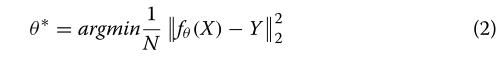
??函数f的选择和用于求解方程(2)的优化策略是具有更好的准确性、稳定性和可解释性的预测模型的关键。在下一节中，我们将提出一种专为实现这一目标而设计的深度神经网络。首先，让我们考虑最直接的基线来模拟函数f——线性回归(linear regression, LR)模型，其中每个代谢物的丰度被预测为所有可用微生物的线性组合：

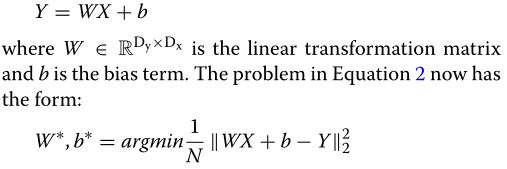
??虽然LR是最简单的模型，但它的缺点是操作一个完整的变换矩阵。大量的参数(即权重)不仅使LR在小而高维的数据集时容易过拟合，而且使模型难以解释。为了降低线性变换矩阵的密度，可以添加Lasso正则化约束以减少变换矩阵W[29]中的有效(即，非零)权重的数量。通过这种正则化，目标函数变成

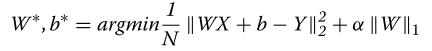
其中，超参数α控制模型的稀疏性，||W||1是线性权重的L1范数。图1b显示了Lasso模型的一个示例。

Our model: a sparse neural encoder-Decoder for data integration

??虽然简单且易于解释，但单变量多组学模型依赖于一个主要假设，即微生物影响代谢物的过程是单一的且彼此独立。另一方面，神经网络可以学习控制两种模式之间动态、多阶段交互的全局过程的许多子过程。
??学习多变量-多变量关系的传统方法是典型相关(CanCor)分析，但是和LR一样，它只能找到数据模态之间的线性关系。因此，我们提出构建一个健壮的、可解释的深度神经网络。我们的模型旨在放松LR和CCA背后的关键假设：这两种数据模式之间存在直接和线性的关系。这一放松将通过两个假设扩展我们对预测模型的表示：
1.在将微生物转化为代谢物的过程中，存在起作用的中间因子。
2.这些因素之间的转换可能包含非线性部分。

1.The neural encoder-Decoder (NED) network

??神经编解码器(NED)结构的目标是通过一个称为潜在特征空间的中间表示，利用来自一个多变量过程的信息来预测另一个多变量随机过程。网络中将相关信息从输入(即微生物)提取到潜在空间的部分称为编码器。网络中预测潜在空间的输出(即代谢物)的部分称为解码器。潜在特征空间被实现为位于编码器和解码器之间的窄隐层。与线性回归等直接线性模型相比，编解码器网络应该具有更稳健的表示，因为权值经历了非线性激活。因此，我们预计NED会表现得更好。
??为了保持模型的可解释性，并使其对少量训练数据更具鲁棒性，我们将隐含层数限制为1。我们的初步实验表明，大量的隐含层并没有改善NED的预测性能，因为该模型隐层过多很容易在有限的训练数据上过度拟合。
??在操作中，模型的两个部分顺序地一起工作。首先，编码器通过编码函数从微生物X中提取相关信息以存储在潜在变量Z中，该编码函数由线性核We和固定的非线性激活函数σe组成：

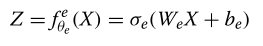
然后，解码器使用类似的解码函数对Z中的潜在内容进行解密，来作为Y的预测值?Y：

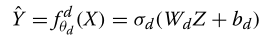
最终的预测模型是编码器和解码器的组成：

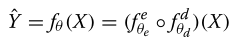
将使用下面的损失函数来训练这个模型：

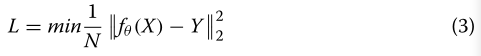
使用优化的参数集θ：

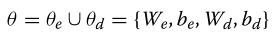
??图1将NED的计算网络与其直接线性对应网络进行了比较。设{xi}i=1，2，…，Dx表示X的Dx分量，并设{yj}j=1，2，…，Dy表示Y的Dy分量。潜在变量的个数Dz是一个可由启发式选择 的元参数(meta-parameter, 虽然我们先验设置Dz=70)。为了提高健壮性和可解释性，首选连接较少的模型。LR模型具有LR有Dx.Dy连接，而NED有Dx.Dz+Dz.Dy连接。因此，我们可以看到，当Dz<<Dx和Dy时，NED<LR。这使得NED不太可能过度拟合，并且更容易解释。我们可以使用稀疏过程进一步降低NED网络的密度，该过程消除了层之间的冗余连接。

2.Sparsifying the nED network

??为了进一步提高模型的稳定性和可解释性，我们试图学习一个有效权数最少的NED模型：一种更稀疏的神经网络，其中大多数权值等于零。近年来，稀疏神经网络的研究取得了重大进展。这项工作的动机是这样一种直觉，即深度网络通常是过度完备的，而稀疏网络可以减少计算开销[30]。此外，稀疏的深度网络也可以简化底层过程的可解释性[31，32]。实现更稀疏网络的主要方法要么修剪不必要的权重[33]，要么加强稀疏性约束作为额外的调节损失[34]。为了将NED稀疏化为一种新的模型，称为稀疏NED，我们采用了一种类似于Lee等人[35]最先提出的单次剪枝策略的预训练筛选 方法。
??Sparse-NED的学习包括两个阶段:筛选和训练。在筛选阶段，我们识别在从微生物丰度中提取预测代谢产物丰度所需信息时最有用的关联。所有其他连接都被标记为不必要的。在训练阶段，使这些冗余链路从前向和后向操作中停用（具体代码实现不理解？？？） 。
??筛选阶段从在全连接模型上的一次训练迭代开始，其中通过对样本数据集D的反向传播来估计损失L(来自公式3)的导数g(w;D)。这些导数是评估连接重要性的关键，因为当连接处的导数具有高幅度时，该连接将对损失具有可测量的影响，因此对代谢物丰度的预测更加显著。与[35]略有不同的是，我们使用所有可用的训练数据，而不是只使用一个小批次作为D来进行灵敏度计算。每个连接Sc的显著性？？？ 被计算为导数的归一化幅度：

??接下来，将网络中的连接按sc的降序进行排序，保留top-k个连接（代码的top-k是根据相关性排序？？？）用于网络训练和推断。保持的连接数量k通过相对于全连接网络中的连接总数的稀疏级别β来控制。k = β|θ| 超参数β是为了平衡模型的精确性和稀疏性。在我们的实验中，我们选择了一个β，以便在和其他稀疏模型比较时，活动(即非零)连接的数量是差不多。使用剩余的连接，稀疏NED通过反向传播进行训练。图1D显示了一个稀疏-NED的例子。
??有趣的是，隐藏节点可能会丢失所有传入连接，导致其被隔离。例如，当隐藏节点多于表示所有潜在信息所需的数量时，可能会发生这种情况。尽管我们在实验中没有预料到这一点，但节点隔离将是有利的，因为这将意味着模型发现的多模态关系具有较低的排名(即，由更少的变量表示)；较低的排名有助于更好地解释模型。节点隔离还可以使稀疏-NED模型对潜在空间大小的变化更具弹性：如果实践者指定了过多的隐藏节点，节点隔离可能会导致多余的节点在训练期间自动停用，只留下必要的节点。

3.The non-Negative weights constraint

??由于活动连接数量较少，稀疏NED比完全连接的NED更容易理解。然而，在其余的连接中，许多都自发地具有负权值。这些神经网络中的负面连接被理解为抑制了对来自一层的因素如何影响另一层[36]的分析。为了提高网络的可解释性，可以使用非负约束来防止权值降至零[37]以下。在我们的应用中，非负权重为微生物丰度对编码器和解码器中的代谢物丰度的贡献提供了更清晰的含义，因为其贡献总是正的。
??为了实现这一观点，我们在每个训练迭代中，通过将参数的估计固定在[0，∞)，对稀疏-NED模型应用非负约束:

??在我们的实验中，我们观察到非负约束不仅提高了模型的可解释性，而且对模型的整体适宜性和稀疏性也有有利的影响。当强制权重为正或零时，每层中的节点往往会相互竞争影响。这实际上使 稀疏-NED 更加稀疏。

Model evaluation

??为了深入理解细菌-代谢关系，我们需要一个不仅准确，而且可高度解释的模型，其解释在不同的数据折叠中是稳定的。在本节中，我们将讨论用于评估我们的预测模型的三个标准：准确性、稀疏性和稳定性。
Accuracy 预测模型fθ的准确性是通过计算预测的代谢物丰度?Y=fθ(X)与实测丰度Y（前10个最佳预测代谢物对应的实测丰度 ）之间的皮尔逊相关系数来得到的。与基于强度的标准相比，相关系数不受信号中使用的尺度的影响，并且在不同的数据归一化方法中是可靠的。为了减少伪相关性的影响，通常使用CLR变换后的数据来计算相关性。对于所有的实验，我们使用了五折交叉验证方案，在五个不同的80%-20%的训练-测试集上验证了模型，并报告了平均准确率。
Sparsity fθ的稀疏性通过模型中活动的线性连接数Cfθ来衡量。在NED及其变体的情况下，它包括来自编码器和解码器网络部分的权重。
Stability 虽然准确性和稀疏性是预测模型的期望属性，但只有当它们在训练集组成的变化中保持一致时，它们的性能和解释才是可靠的。对于每个模型家族，我们通过测量模型参数θ在不同训练集上的平均成对相似性[38]来评估预测模型的稳定性。具体地说，我们将数据集划分为5块，并在每一块中学习一个模型实例。然后，对于每对模型实例，计算模型参数之间的皮尔逊相关系数。方法稳定性的主要度量，即稳定性指数，是通过模型族中所有模型实例对之间的平均相似度来计算的。
??为了集中考虑模型体系结构的稳定性，我们使用模型中每两层之间的二元（0或1）连接邻接矩阵来计算稳定性指数。对于全连接的模型(例如，线性回归或CanCor)——其中一层中的每个因素都会影响后续层中的每个因素——二元连接矩阵包含全部1。因此，稳定指数总是等于1（代码跑出来的mean_ci确实为1，背后的原理不理解？？？）。对于稀疏方法(例如，Lasso和NED)，稳定性指数衡量跨层连接的一致性和可靠性。对于像NED及其变体这样的多层模型，我们使用第一个模型实例来初始化其他实例的训练，以便我们保持中间层变量的对应(例如，划分块1中的潜在变量“V5”与划分块2中的潜在变量“V5”相同)。

Interpretation of network layers

??神经网络包含三个层次:微生物输入层、隐藏层(即潜层)和代谢产物输出层。为了理解潜在空间的性质，我们对每一层进行了单独的分析，并比较了它们的结果。所有的微生物和代谢产物分析都是在clr转化数据上进行的，而潜空间分析则是在未改变(即tanh压缩，激活函数)数据上进行的。

1.Differential abundance (DA) analysis

??我们对三个实验组[溃疡性结肠炎(UC)、克罗恩病(CD)和健康对照组(HC)]的微生物、代谢物和潜在空间特征集(分别)进行方差分析(ANOVA)。我们认为FDR调整后的p值p<0.05的任何特征都是显著的。请注意，先前的clr变换使相对数据的单变量统计检验有效，只要结果相对于所使用的参考能得到解释[26，27]。

2.Redundancy analysis (RDA)

??我们使用R包vegan[39]中的RDA函数(分别)对微生物、代谢物和潜在空间特征集进行了冗余分析(RDA)。

3.Random forests

??我们使用微生物、代谢物和潜在空间特征来训练一个随机森林分类器来预测几个双因素结果(见下一节结果和讨论)。随机森林模型使用R包randomForest[40]中的randomForest函数进行训练，没有任何特征选择或超参数调整。对于每个特征空间和每个结果，我们比较了使用R包exprso[41]的plMonteCarlo函数拆分的25个随机子样本测试集的平均“out-of-the-box”AUC。

结果和讨论

Summarization preserves data structure

??像NGS和LC-MS这样的高通量分子分析产生的数据集通常比样本有更多的特征。在统计学上，高维是一个问题，因为每增加一次测试，错误发现的可能性就会增加。在机器学习中，高维增加了过度拟合的可能性，也使结果模型更难解释。因此，在训练模型之前减少特征的数量是明智的。在去除零值特征后，我们使用领域知识将剩余的特征聚合成具有生物学意义的组。对于代谢物，我们使用功能聚类；对于细菌，我们指定属。表1描述了数据处理前后的维度。
??图2显示了代谢物数据(上)和微生物组数据(下)的前两个主成分，使用“Complete”(左)和“Summarized”(右)管道进行处理。在这里，我们看到，使用领域知识将代谢物聚集成类，将细菌种类分类到属，似乎并没有改变数据的基本结构。为了量化两条管道之间的一致性，我们计算了“Complete”样本间距离和“Summarized”样本间距离之间的皮尔逊相关性。我们发现，对于代谢物(ρ=.903)和微生物(ρ=.674)而言，“Summarized”的样本间距离与“Complete”距离一致。发现微生物数据有更大的不一致性，可理解为在同一属内的不同细菌物种可以占据不同的生态位。
??另外，我们发现就IBD患者聚类情况而言，他们的肠道代谢物比他们的肠道细菌聚集更明显。事实上，代谢数据的差异丰度分析揭示了128个(总共143个)显著代谢物类别，而只有15个(总共51个)显著细菌属(完整列表见附录)。**表2（？？？）**显示了选定细菌属经CLR转化后的平均丰度，选择这些细菌属，是因为它们已被发现与IBD有关。两个属，反刍球菌属和梭杆菌属，显示出与过去文献一致的联系[42]。

Microbe abundance predicts metabolite abundance

??由于代谢物和细菌都与IBD有关，因此探讨它们之间的相互依赖关系是很有意义的。在引言中，我们描述了四种整合多组学数据的方法：单变量-单变量回归、单变量-多变量回归、多变量-多变量回归和神经网络。Franzosa等人证实了这些数据的弱单变量-单变量回归[14]。在这里，我们通过5折交叉验证对微生物-代谢物预测模型性能进行基准测试，来评估其他多组学方法的性能。定量评价是使用“Model evaluation”中描述的三个标准进行的。
神经编解码器的性能优于线性回归
??我们不指望微生物群本身就能预测所有代谢物的丰度。相反，我们的动机是回答两个研究问题：(1)微生物群可以预测哪些代谢物？以及(2)这一预测的可靠性有多高？**表3（“Complete”数据）和表4（“Summarized”数据）**显示了微生物-代谢物预测模型的性能。表格按使用的多组学整合方案组织：单变量-多变量、多变量-多变量或神经网络。为了回答这两个研究问题，我们比较了每个模型对前10个最佳预测的准确性，以及它的稀疏性和稳定性。
稀疏性提高了精确度和可解释性
??如果没有正则化，模型很容易过度拟合。因此，稀疏线性回归(即Lasso)和稀疏神经编解码器的性能优于全连接的相应模型。然而，在这两种情况下，神经编解码器的表现都优于线性回归(尽管Lasso的表现也不错)。
非负权重提高了可解释性
??默认的线性回归和神经编解码器网络，权重可以取任何值。在这里，我们建议使用非负权重约束来提高模型的可解释性。对于神经网络，此约束意味着当输入节点对隐藏节点有贡献时，该贡献始终是累加的。这允许我们将隐藏层解释为输入活动的聚合，同样每个输出节点都被计算为隐藏节点活动的聚合。结合稀疏性，非负权重约束确保每个节点是几个元素的简单求和。表3和表4显示该限制不会严重降低准确性，此外它有利地迫使网络变得更加稀疏。

The latent space is clinically coherent

??编码-解码器网络的潜在空间是对输入数据的抽象学习，旨在描述肠道微生物如何与所有患者的肠道代谢物相关联 （或在所有患者中肠道微生物是如何与肠道代谢物相关联的）。因此，隐藏层内的差异反映了微生物-代谢物轴内的患者间差异。我们重点关注稀疏和非负的神经编解码器模型，使用“Summarized”数据进行训练，因为我们认为它很好地平衡了准确性和可解释性。对于该神经网络，每个隐节点的值等于tanh(x·w+b)，其中x是每个样本的微生物丰度，w是与每个微生物相关的权重，b是偏移量。这些隐藏节点共同构成了一个新的特征空间，以完全无监督的方式学习，可以用常规的统计建模直接进行分析。
潜在空间与IBD相关
??对于隐含层中的70个节点中的每一个，我们可以计算所有患者的方差 ：一些节点比其他节点更易变。我们还可以计算进出每个节点的权重 ：一些节点比其他节点有更多的“流量”。高流量节点将多种微生物与多种代谢物紧密地联系在一起，而低流量节点描述的关系较少或更微弱。图3绘制了节点方差与节点流量的关系图。在这里，我们看到高方差节点通常是高流量节点，这表明模拟微生物代谢相互作用最强的节点在个体患者之间的差异也最大。潜在特征的方差分析表明，高方差-高流量节点与IBD显著相关(FDR调整后的p值<0.05)。由于潜在空间是微生物和代谢物之间关系的抽象，它与IBD的相关性表明，微生物和代谢物之间的关系本身就与IBD有关。
潜在空间是一个噪声过滤器
??方差分析(ANOVA)允许我们测量潜在空间与IBD之间的统计关联性，我们还可以通过冗余分析(RDA)进一步了解潜在空间的临床相关性。RDA是一种主成分分析，它约束主轴，使它们描述潜伏空间的一部分，也被解释为“条件矩阵”L。这里，条件矩阵包含临床协变量：年龄、粪便钙保护素、诊断、抗生素使用、免疫抑制剂使用、美沙拉明使用、类固醇使用。在图4左侧面板中，我们看到第一个RDA轴包括多个相关节点，这些节点都与IBD诊断密切相关(CD vs.HC vs.UC)。虽然用药会混淆诊断，但我们看到离轴结点“V21”与抗生素使用(和CD)完全反相关，而离轴结点“V66”与其相关。图4右侧面板显示一些最长的第一轴和离轴箭头的框图。通过观察RDA特征值，我们发现26.9%的潜在空间可以用临床协变量L来解释；而超过12%微生物数据，23.6%的代谢物数据可以用临床协变量L来解释。换句话说，隐层比输入或输出层更能解释临床协变量。这一发现由两个假设支持。（1）微生物和代谢物之间的关系本身与IBD有关。（2）编解码器潜在空间就像一个噪声过滤器，可以完全无监督地提取源数据中与临床相关的部分。
潜伏空间是有识别力的
??从我们的差异丰度分析中， 我们知道微生物、代谢物和潜伏特征都与IBD相关(尽管代谢物关联多于微生物关联)。虽然我们已经证明了潜在空间与临床相关，但我们还想进一步证明它在分类任务中的区分能力。表5显示了在25个随机子样本训练集上训练的二进制分类器的平均“out-of-the-box”AUC。在大多数结果中，潜在空间分类器的性能至少和微生物分类器一样好。然而，当预测抗生素和免疫抑制剂的使用时，隐藏层实际上比微生物或代谢物的丰度更具预测性。
潜在空间是可解释的
??图5显示了将微生物与代谢物联系起来的三层图，该图使用所有5个训练集划分块上的边缘重叠来构建 。中间层包含对微生物丰度进行加权的潜在变量，以便最大限度地预测代谢物丰度。这张图揭示了一个总体结构：上半部分描述了富集在健康肠道中的微生物如何预测也富集在健康肠道中的代谢物，而下半部分描述了在健康肠道中减少的微生物如何预测在健康肠道中也减少的代谢物。反刍球菌和梭杆菌(Ruminococcus and Fusobacterium）都是IBD的复制型生物标志物，它们与代谢产物相关的潜在变量也与IBD相关。
??在图的上半部分，我们看到瘤胃球菌(以及其他)如何影响6个潜在变量，进而预测几种健康的代谢物特征，包括托烷生物碱和甾体皂甙，以及其他植物衍生化合物。有趣的是，尽管可能并不令人惊讶，一些富含在健康肠道中的植物衍生化合物具有已知的药用特性[43，44]。在图的下半部分，我们看到梭杆菌(以及其他)是如何影响1个潜在变量的；节点V61，高度预测了胆汁酸、酒精和衍生物的丰度。这一发现与文献一致，即胆汁酸结合牛磺酸是细菌新陈代谢的底物，牛磺酸副产物的解毒缺陷与溃疡性结肠炎有关[45]。