[人工智能]sklearn入门——回归树

重要参数、属性及接口

• criterion
  回归树衡量分支质量的指标，支持的标准有三种：
  1）输入“mse”使用均方误差(mean squared error)，父节点和子节点之间的均方误差的差额来作为特征选择的标准，通过使用叶子节点的均值来最小化L2损失。
  2）输入"friedman_mse"使用费尔德曼均方误差，这种指标使用费尔德曼针对潜在分支中的问题改进后的均方误差。
  3）输入"mae" 使用绝对平方误差，使用节点的中值来最小化L1损失
  其他属性也包括feature_importances_,接口有apply,fit,predict,score等核心的。
  $$MSE=\frac{1}{N}\sum _{i=1}^N(f_i?y_i{)}^2$$

  在回归树中MSE既是分支质量的衡量标准也是回归树回归质量的标准，在回归中，MSE越小越好，而接口score返回的是R²,R²定义是：
  $R^2=1?\frac{u}{v},u=\sum (f_i?y_i{)}^2,(残差平方和)v=\sum (y_i?y_{hat})(总平方和)$,其中y-hat是所有标签的平均值。
  虽然均方误差恒为非负，但考虑到作为损失，变成了负的。

交叉验证

交叉验证是用来观察模型的稳定性的一种方法，将数据划分为n份，依次使用其中的一份作为测试集，其他n-1份作为训练集，多次计算模型的准确性来评估模型的平均准确程度。（这吃瓜的时候学过，现在听到居然毫无印象。。。。）
相关操作：

from sklearn import tree
# 交叉验证的库
from sklearn.medel_selection import cross_val_score
# 随便搞一个数据集
from sklearn.datasets import load_boston

# 实例化一个回归模型
regressor = tree.DecesionTreeRegressor(random_state=0)
# 参数分别是实例化的模型，样本数据矩阵，样本标签，验证次数，衡量标准（这里是均方误差的相反数）
cross_val_score(regressor, boston.data, boston.target, cv=10,scoring='neg_mean_squared_error')

回归树的例子

用回归树拟合正弦函数曲线

import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
rng = np.random.RandomState(1) # 随机数种子
X = np.sort(5*rng.rand(80,1), axis=0)
# y数据必须是一维的，用ravel()展平
# numpy数组中一维数组不分行和列
y = np.sin(X).ravel()

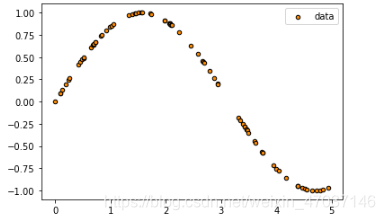
plt.figure()
# plt.scatter专门画散点图
plt.scatter(X, y, s=20, edgecolor='black', c='darkorange', label='data')
plt.legend()

# np.random.rand(数组结构),生成随机数组的函数
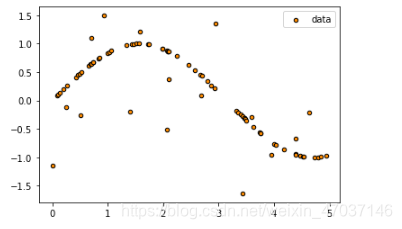
# 加噪声
y[::5] += 3*(0.5-rng.rand(16))

plt.scatter(X, y, s=20, edgecolor='black', c='darkorange', label='data')
plt.legend()

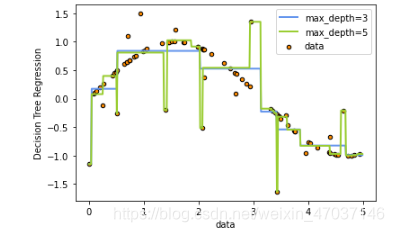
regressor1 = tree.DecisionTreeRegressor(max_depth=3)
regressor2 = tree.DecisionTreeRegressor(max_depth=5)
regressor1.fit(X, y)
regressor2.fit(X, y)

X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regressor1.predict(X_test)
y_2 = regressor2.predict(X_test)

plt.figure()
plt.scatter(X, y, s=20, edgecolor='black', c='darkorange', label='data')
plt.plot(X_test, y_1, color='cornflowerblue', label='max_depth=3', linewidth=2)
plt.plot(X_test, y_2, color='yellowgreen', label='max_depth=5', linewidth=2)
plt.xlabel('data')
plt.ylabel('Decision Tree Regression')
plt.legend()
plt.show()