第三周:浅层神经网络(Shallow neural networks)
文章目录
- 第三周:浅层神经网络(Shallow neural networks)
- 前言
- 正文
- 3.1 神经网络概述( Neural Network Overview)
- 3.2 神经网络的表示( Neural Network Representation)
- 3.3 计算一个神经网络的输出( Computing a Neural Network's output)
- 3.4 多样本向量化( Vectorizing across multiple examples)
- 3.5 向量化实现的解释( Justification for vectorized implementation)
- 3.6 激活函数( Activation functions)
- 3.7 为什么需要非线性激活函数?( why need a nonlinear activation)
- 3.8 激活函数的导数( Derivatives of activation functions)
- 3.9 神经网络的梯度下降( Gradient descent for neural networks)
- 3.10(选修)直观理解反向传播 (Backpropagation intuition)
- 3.11 随机初始化( Random+Initialization)
- 总结
前言
主要内容:吴恩达《Deep Learning》系列的第一门课《神经网络和深度学习》的第三周部分:浅层神经网络简介:本文是笔者在学习该课程的过程中随意记录的一些要点,希望能帮助到大家,欢迎大家留言or私信讨论
参考资料:吴恩达先生的课程材料&黄海广先生整理的深度学习课程笔记(V5.7)
正文
以下是本篇文章正文内容
3.1 神经网络概述( Neural Network Overview)
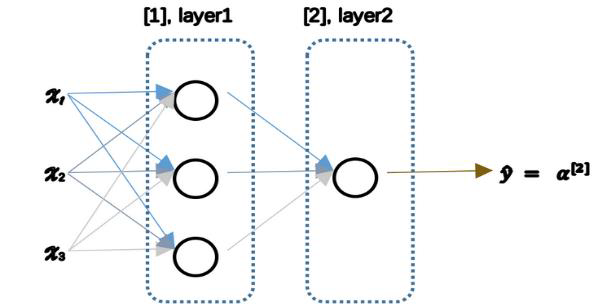
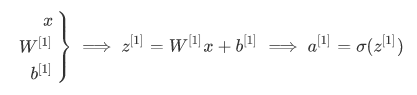
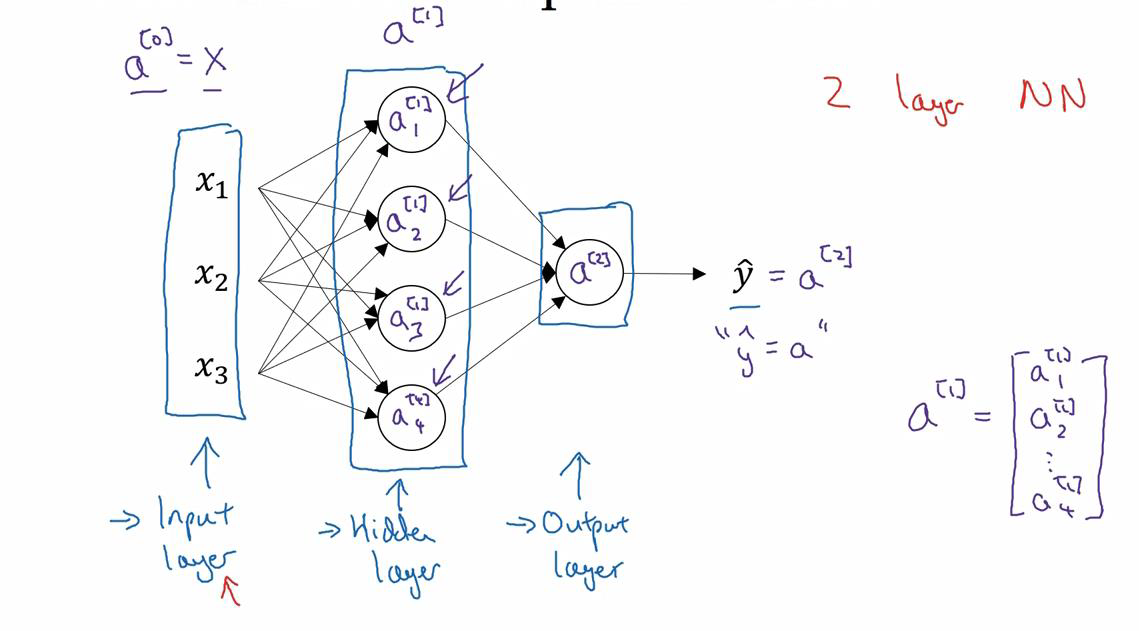
3.2 神经网络的表示( Neural Network Representation)
一、
当我们计算网络的层数时,输入层是不算入总层数内,所以隐藏层是第一层,输出层是第二 层
二、
我们将输入层称为第零层
3.3 计算一个神经网络的输出( Computing a Neural Network’s output)
单一样本

3.4 多样本向量化( Vectorizing across multiple examples)
多个样本
? 逻辑回归是将各个训练样本组合成矩阵,对矩阵的各列进行计算。神经网络是通过对逻辑回归中的等式简单的变形,让神经网络计算出输出值。这种计算是所有的训练样本同时进行的,以下是实现它具体的步骤:
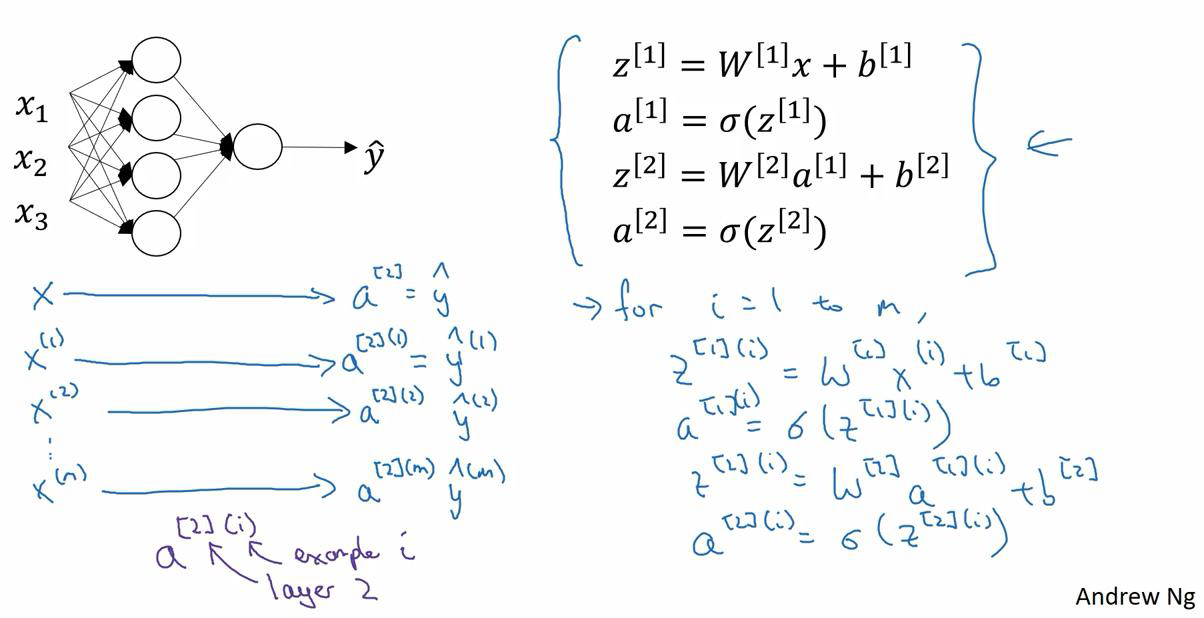
向量化


3.5 向量化实现的解释( Justification for vectorized implementation)

3.6 激活函数( Activation functions)
a = t a n h ( z ) = e z ? e ? z e z + e ? z a=tanh(z)=\frac {e^z-e^{-z}}{e^z+e^{-z}} a=tanh(z)=ez+e?zez?e?z?
? tanh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后,穿过了(0,0)点,并且值域介于+1和-1之间。
? 在训练一个算法模型时,如果使用tanh函数代替sigmoid函数中心化数据,使得数据的平均值更接近0而不是0.5。
? 优化算法中:tanh函数在任何时候都优于sigmoid函数
? 但有一个例外:在二分类的问题中,对于输出层,因为𝑦的值是0或1,所以想让 y ^ \widehat{y} y ?的数值介于0和1之间,而不是在 -1和 +1之间。所以需要使用sigmoid激活函数。
? sigmoid函数和tanh函数两者共同的缺点是,在𝑧特别大或者特别小的情况下,导数的梯度或者函数的斜率会变得特别小,最后就会接近于0,导致降低梯度下降的速度。
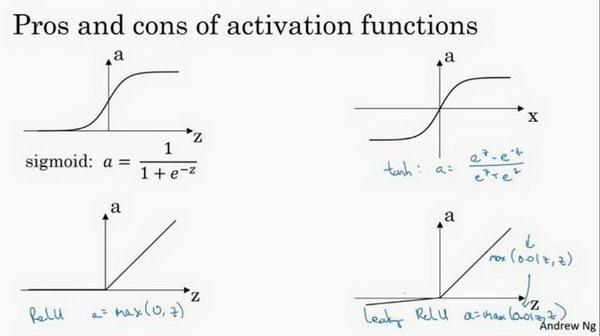
? 如果输出是0、1值(二分类问题),则输出层选择sigmoid函数,然后其它的所有单元都选择Relu函数。
? Relu函数和Leaky Relu函数



3.7 为什么需要非线性激活函数?( why need a nonlinear activation)

? 总而言之,不能在隐藏层用线性激活函数;唯一可以用的通常是输出层
3.8 激活函数的导数( Derivatives of activation functions)
(1)Sigmoid activation function
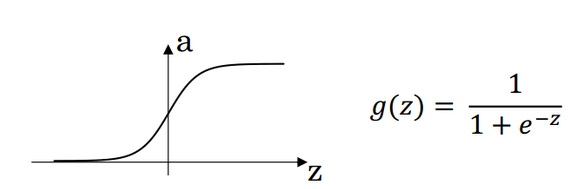
a = g ( z ) a=g(z) a=g(z)
d d z g ( z ) = a ( 1 ? a ) \frac {d}{dz}g(z)=a(1-a) dzd?g(z)=a(1?a)
(2)Tanh activation function
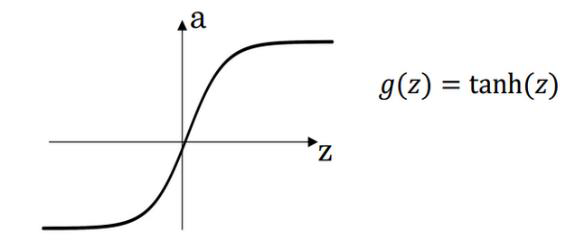
g ( z ) = t a n h ( z ) = e z ? e ? z e z + e ? z g(z)=tanh(z)=\frac {e^z-e^{-z}}{e^z+e^{-z}} g(z)=tanh(z)=ez+e?zez?e?z?
d d z g ( z ) = 1 ? ( t a n h ( z ) ) 2 \frac{d}{dz}g(z)=1-(tanh(z))^2 dzd?g(z)=1?(tanh(z))2
注:当 z = ± 10 z=±10 z=±10时 d d z g ( z ) ≈ 0 \frac{d}{dz}g(z)≈0 dzd?g(z)≈0
? 当 z = 0 z=0 z=0时 d d z g ( z ) = 1 ? ( 0 ) = 1 \frac{d}{dz}g(z)=1-(0)=1 dzd?g(z)=1?(0)=1
(3)Rectified Linear Unit(ReLU)
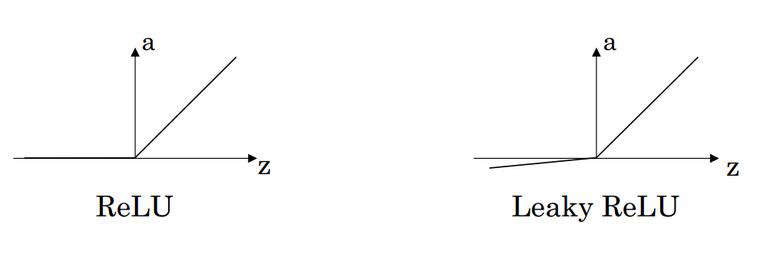

(4)Leaky Linear Unit(Leaky ReLU)

3.9 神经网络的梯度下降( Gradient descent for neural networks)
3.10(选修)直观理解反向传播 (Backpropagation intuition)
3.11 随机初始化( Random+Initialization)
? 当你训练神经网络时,权重随机初始化是很重要的。对于逻辑回归,把权重初始化为0当然也是可以的。但是对于一个神经网络,如果你把 权重或者参数都初始化为 0,那么梯度下降将不会起作用。
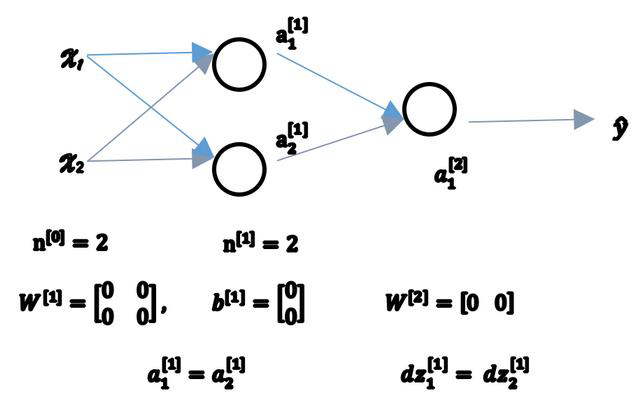
? b可以初始化为0,但W不行,一旦W=0,会导致反向传播中dZ1=dZ2,从而导致梯度下降无法继续
? e.g.

总结
以上就是神经网络的编程基础(第二周)的部分学习笔记,本文仅仅简单记录了在学习过程中个人认为比较重要的要点。