[人工智能]机器学习之三（读书笔记）

• Binary-class Classification
• 逻辑斯蒂回归
• Multi-class Classification

五、Classification:Probabilistic Generative Model

在分类中找一个function，它的input是一个object x，它的output是这个object属于哪一个class。

task：在金融上，通过某个人的信息决定要不要借钱给他；医疗诊断；手写字辨识；人脸辨识；

以下以宝可梦为例，输入一个宝可梦输出它是哪一类：

1.将宝可梦数值化放到function中，即特性数值化：
Total（多强）、HP（生命值）、Attack（攻击）、Defense（防御）、SP Atk（特殊攻击时的攻击力）、SP Def（特殊攻击时的攻防御值）、Speed（速度）；
那么一只宝可梦就是一个7个数字组成的vector（向量）；
2.Training data for Classification

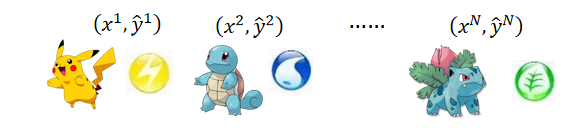
a.建立一个function $f(x)$，内嵌一个函数$g(x)$，$g(x)$>0输出为分类1；$g(x)$<0输出为分类2；
b.定义Loss Function为输出数值为错误的次数；
c.找到最好的function（方法有SVM等）

find best function solution（非SVM）：
两个分类中，x属于分类1的概率（其中$P(C_1)$为从calss1抽出x的几率、$P(C_2)$为从calss2抽出x的几率、$P(x\mid C_1)$从class1中能抽到指定x的几率、$P(x\mid C_2)$从class2中能抽到指定x的几率）：

以上想法叫Generative Model（生成模型，可以算某一个x出现的几率$P(x)=P(x\mid C_1)P(C_1)+P(x\mid C_2)P(C_2)$ ，就可以自己产生x）。

从training data中估测出以上4个几率值：
假设Class1为水系的神奇宝贝，Class2为一般系；400个data中，水系和一般系的当做training data 。剩下的当做testing data；

Training data：79 Water ，61 Normal；

Prior：从Class1里sample出一只宝可梦的概率：
$P(C_1)$ = 79 / ( 79 + 61 ) =0.56；
从Class2里sample出一只宝可梦的概率：
$P(C_2)$ = 61 / ( 79 + 61 ) =0.44；

79只水系宝贝的分布（一个点代表一只）：

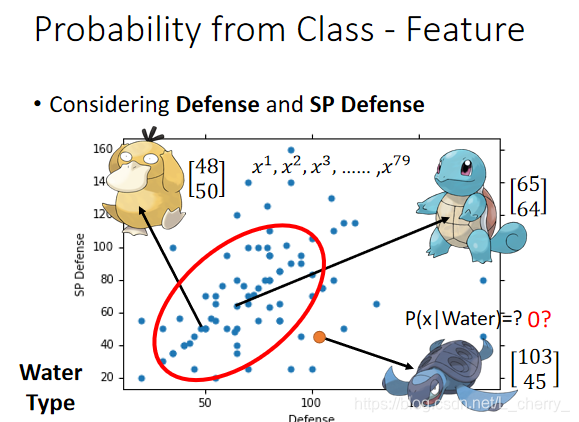
如何计算不在这79个中的海归的$P(x\mid Water)$？
假设这79个点都是从一个Gaussian distribution（高斯分布）中sample出来的，如何通过79个点找到这个高斯分布？

Gaussian Distribution
mean：$\mu$（是一个vector）、covariance（协方差）:$\Sigma$（是一个matrix）；
同样的x，把不同的$\mu$和$\Sigma$代入function，就会有不同的形状；
同样的$\Sigma$、不同的$\mu$，代表它们几率分布最高点的地方是不一样的；

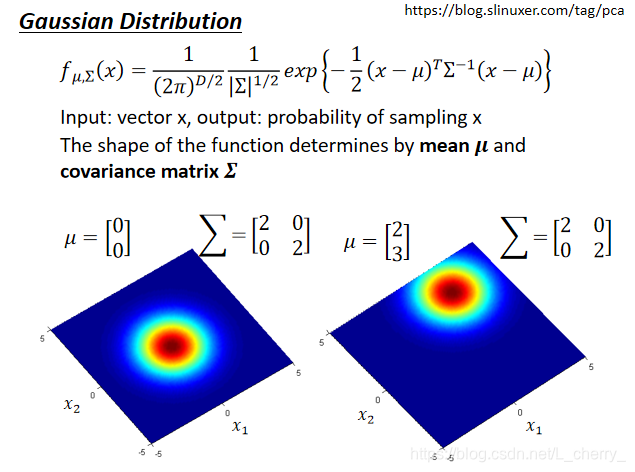
同样的$\mu$、不同的$\Sigma$，代表几率分布最高点是一样的，但是分布，散的程度不一样；

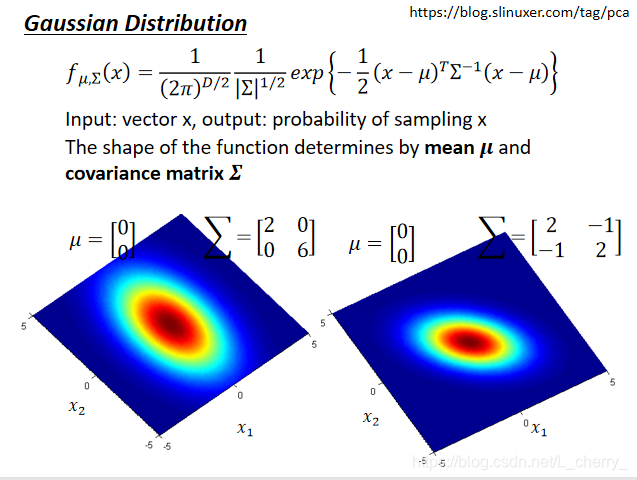
根据79个点估测出Gaussion的mean $\mu$和$\Sigma$，根据以上Gaussion的公式可算出某x从这个Gaussion中被sample出来的几率。

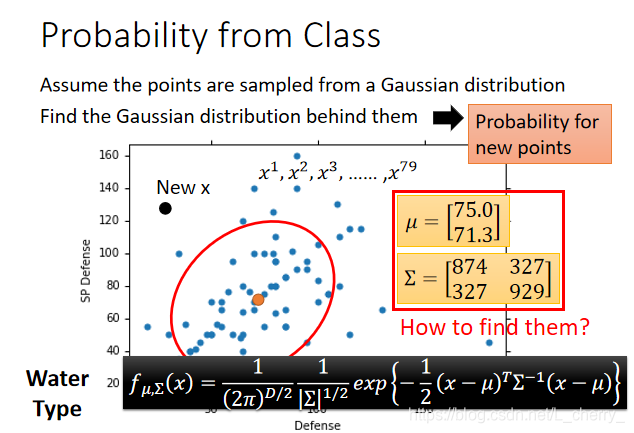
那么怎么找这个$\mu$和$\Sigma$呢？
用Maximum Likelihood（极大似然）的概念：找到likelihood最大的Gaussion。
给一个Gaussion，可以算出这个Gaussion sample出这79个点的几率（likelihood）：
$L(\mu ,\Sigma )=f_{\mu ,\Sigma }(x^1)f_{\mu ,\Sigma }(x^2)f_{\mu ,\Sigma }(x^3)......f_{\mu ,\Sigma }(x^{79})$，其中$f_{\mu ,\Sigma }(x^1)$为从这个Gaussion中sample出第一个点的几率；

likelihood最大的Gaussion写作$({\mu }^{?},{\Sigma }^{?})$：
穷举所有的$\mu$和$\Sigma$看哪个likelihood最大（通过对第二个式子微分=0求极值）

通过以上方法得到两个分类的Gaussion：

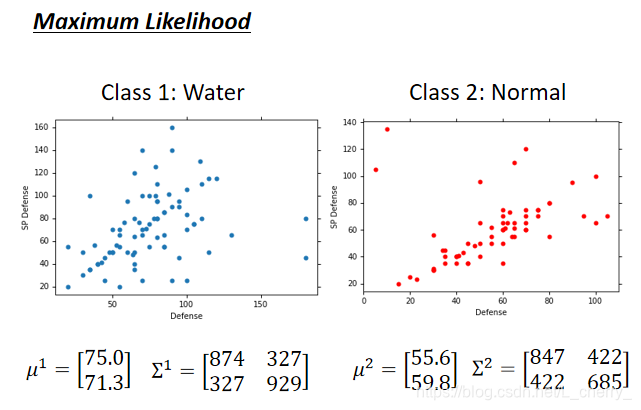
回到分类问题：

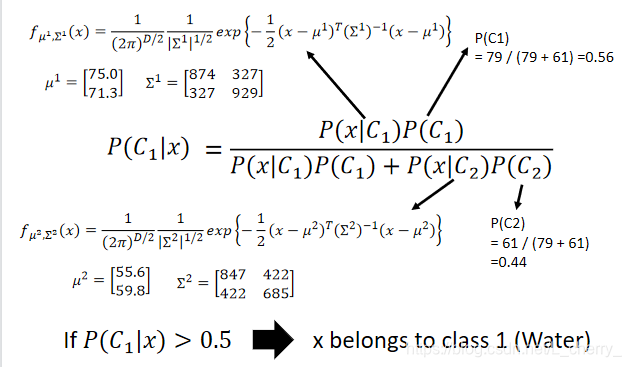
得到的结果在testing data上的正确率是47%（原因是因为feature取的太少，原本应该是7维的）：

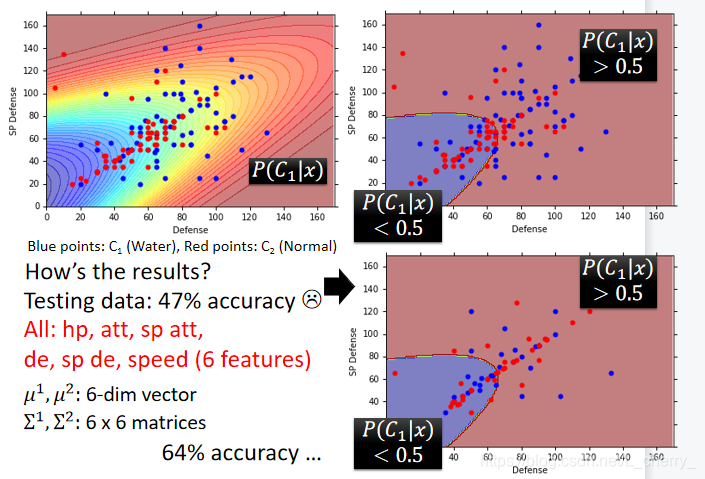
一般不会每个class都给一个Gaussion，一般是share同一个covariance的matrix，即$\Sigma$，这样就可以需要比较少的parameter（防止过度拟合）：

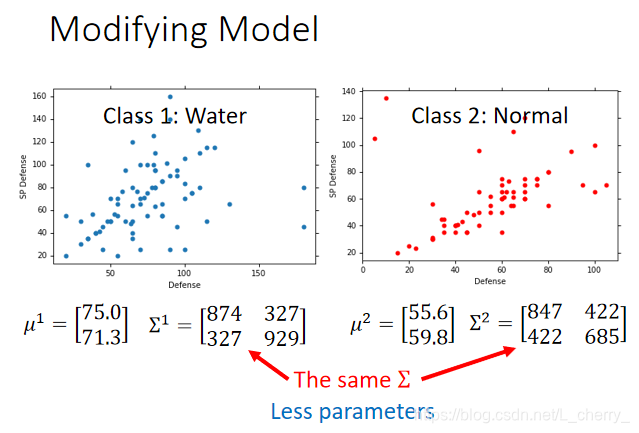
那么这个Gaussion就是：

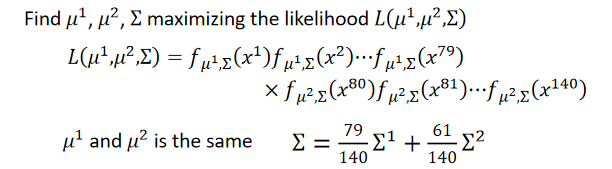
其中${\mu }^1$和${\mu }^2$的算法和之前一样（class1中的x平均起来就变成了${\mu }^1$，class2中的x平均起来就变成了${\mu }^2$），唯一不一样的是$\Sigma$：
$\Sigma =\frac{79}{140}{\Sigma }^1+\frac{61}{140}{\Sigma }^2$（把原来的加起来乘以数目再平均再相加）

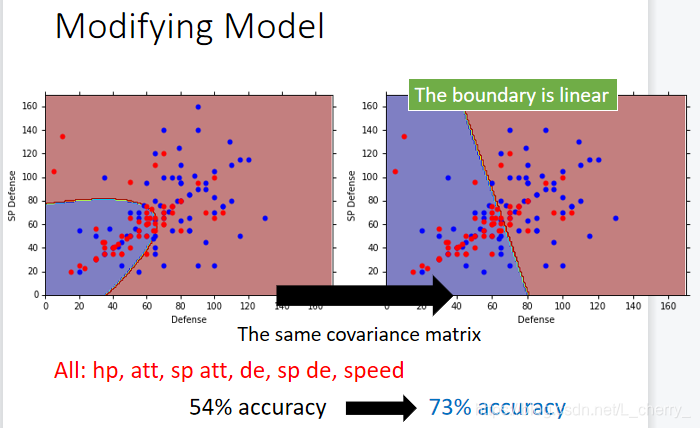
调整后的结果为：

总结：three steps

• Function Set(Model):
  

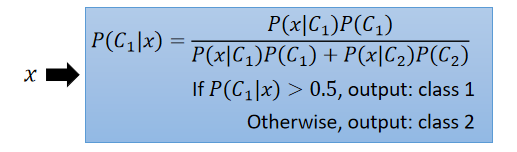
• Goodness of a function:
  找一个probability distribution可以最大化产生data的likelihood

朴素贝叶斯（Naive Bayes Classifier）：假设所有的feature都是independent产生的，不model feature 和feature间covariance的关系，用这种方法做分类，叫做朴素贝叶斯。

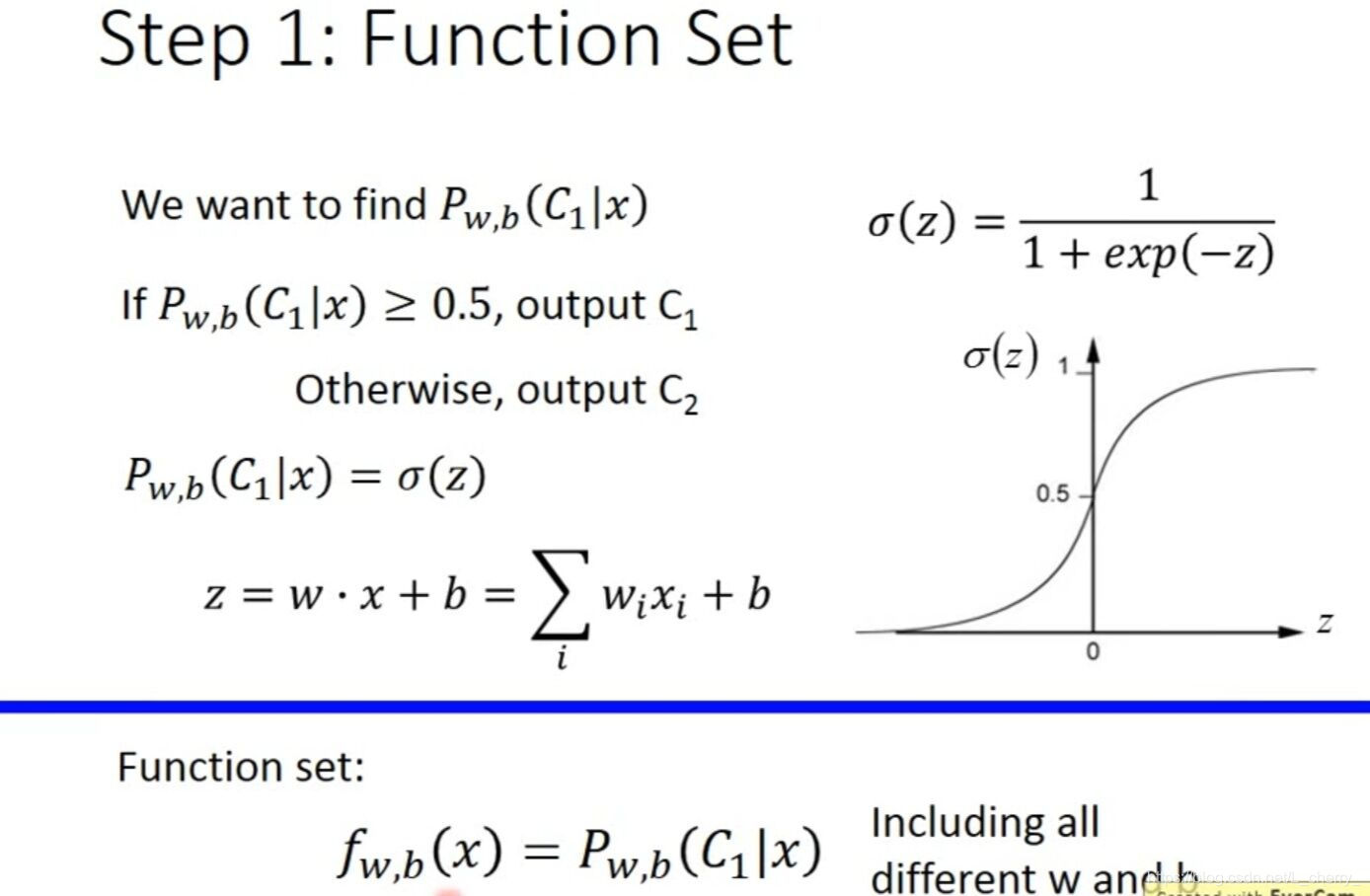
posterior probability（后验概率）：

z越大，sigmoid function（乙状函数）越趋近于1；z越小，sigmoid function（乙状函数）越趋近于0；
通过计算化简得到z：
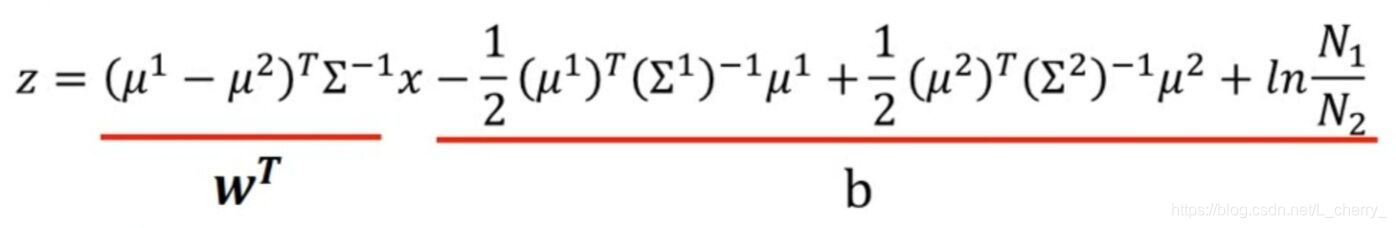那么$P(C_1\mid x)=\sigma (w?x+b)$ （linear）

六、Logistic Regression

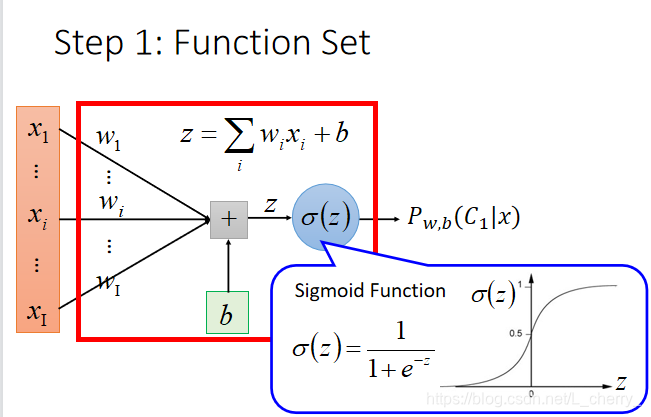
argmax是一种函数，是对函数求参数(集合)的函数。当我们有另一个函数y=f(x)时，若有结果
x0 = argmax(f(x))，则表示当函数f(x)取x=x0的时候，得到f(x)取值范围的最大值；若有多个点使得f(x)取得相同的最大值，那么argmax(f(x))的结果就是一个点集。换句话说，argmax(f(x))是使得 f(x)取得最大值所对应的变量点x(或x的集合)。arg即argument，此处意为“自变量”。

找一个$w$和$b$使得$L(w,b)$最大化，即：

根据以上的数值化后，可得：

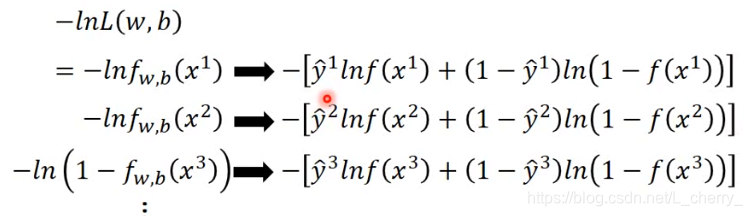
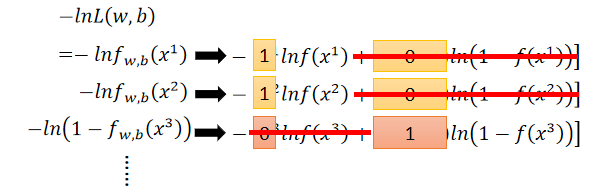
那么损失函数可改写为：

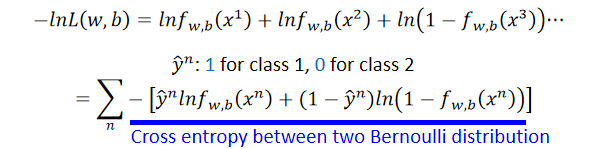
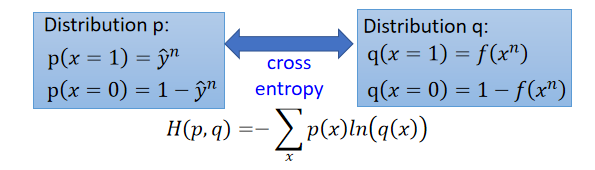
cross entropy between two Bernoulli distribution(两个伯努利分布之间的交叉熵)：
使用Gradient Descent找到最佳function：

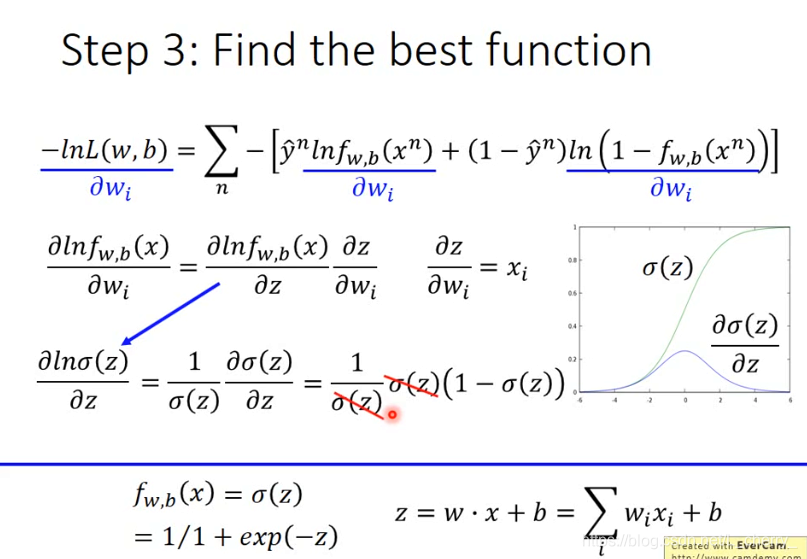
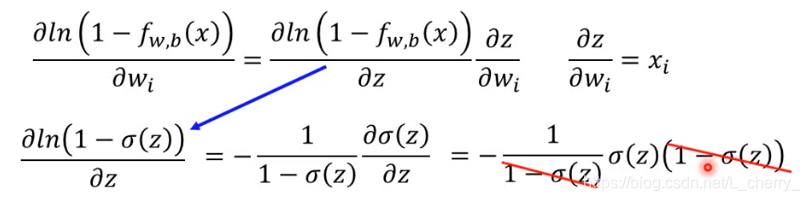得到的式子为：

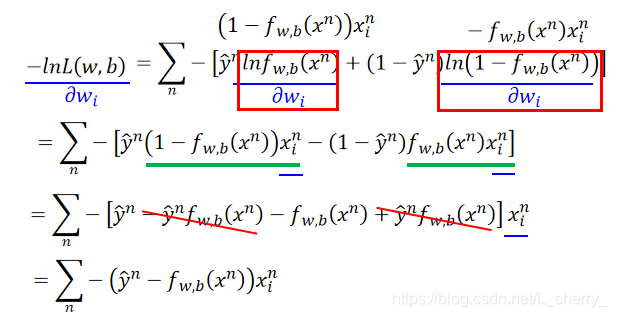
对比Logistic Regression和Linear Regression：

如上图所示，在Step 1 中，两者的Model Function不一样，并且前者的Output值范围在0~1之间，后者的Output值可以是any value；
在Step 2 中，两者的Loss Function不一样，并且前者的$\hat{y}$值为1或0（分类），后者的$\hat{y}$值为实数；
其中前者交叉熵为：

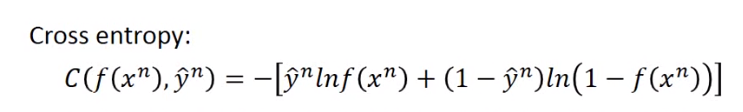
在Step 3中，两者的update方式一致。

Logistic Regression + Square Error（平方误差）：



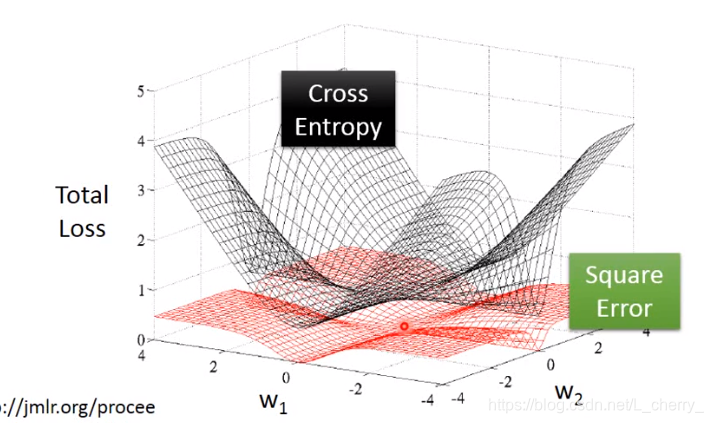
结论：如果使用Square Error无论离目标很近，还是很远，结果都是0，导致update很慢，不容易得到好的结果。

Discriminative v.s. Generative

Logistic Regression的方法称之为Discriminative（判别的）；
用Gaussion描述posterior probability的方法称之为Generative；

1. 两者的Model一样：
   
2. Generative Model的优点：

• 在概率分布假设下,需要更少的training data
• 在概率分布假设下，对噪音更具鲁棒性
• 先验概率和类相关概率可以从不同的来源进行估计

七、Multi-class Classification

假设有三个类别，每个类别都有自己的weight 和 bias；

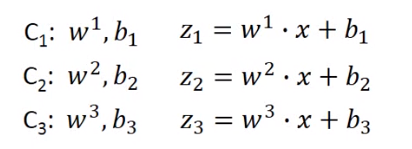
把$z_1,z_2,z_3$丢进Softmax function:
首先将它们指数化，再相加求和得到total sum${\sum }_{j=1}^3{e}^{z^j}$，再将$e^{z^j}$分别除以total sum得到Softmax function的Output：$y_1,y_2,y_3$，如图：

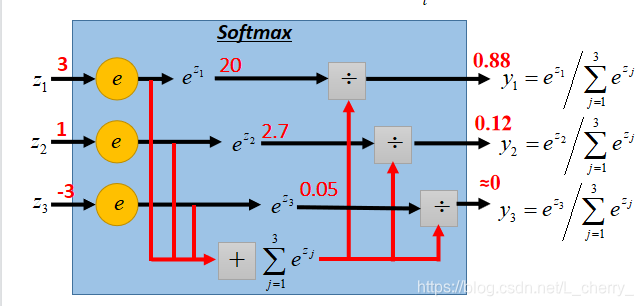
Softmax function的Output特点：

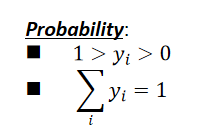
$x$从$C_1$中取出的function为：

总结：

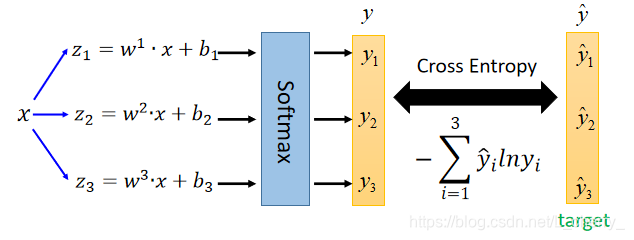
计算$y$$\hat{y}$和Cross Entropy要求$\hat{y}$是一个probilitity distribution （概率分布）：

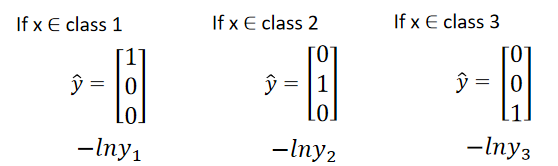
Limitation od Logistic Regression
假设存在一个如下图的Case，四组data，每组data有两个feature，使用Logistic Regression对此做分类：

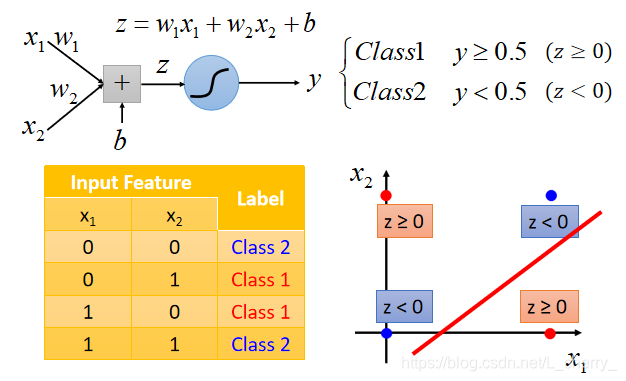
无法做到，因为Logistic Regression的boundary是一条直线，无法把Class1和Class2分到boundary的两边。
但如果坚持用Logistic Regression分类解决办法就是使用Feature Transformation（特征变换）：做一些转换，找一个比较好的feature space

把$\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$转到另一个space，$x_1^{{}^{\prime }}$就是某一个点到$\left[\begin{array}{c}0\\ 0\end{array}\right]$的距离，$x_2^{{}^{\prime }}$就是某一个点到$\left[\begin{array}{c}1\\ 1\end{array}\right]$的距离；
$\left[\begin{array}{c}0\\ 0\end{array}\right]$这个点距离$\left[\begin{array}{c}0\\ 0\end{array}\right]$为0，$x_1^{{}^{\prime }}$=0；距离$\left[\begin{array}{c}1\\ 1\end{array}\right]$这个点为$\sqrt{2}$，$x_2^{{}^{\prime }}$=$\sqrt{2}$，那么$\left[\begin{array}{c}0\\ 0\end{array}\right]$就转移到$\left[\begin{array}{c}0\\ \sqrt{2}\end{array}\right]$这个点；同理$\left[\begin{array}{c}1\\ 1\end{array}\right]$就转移到$\left[\begin{array}{c}\sqrt{2}\\ 0\end{array}\right]$这个点；$\left[\begin{array}{c}1\\ 0\end{array}\right]$和$\left[\begin{array}{c}0\\ 1\end{array}\right]$这两个点都转移到$\left[\begin{array}{c}1\\ 1\end{array}\right]$这个点，如图：

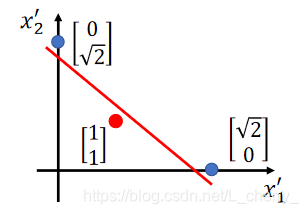
由此可用Logistic Regression分类，缺点是很难找到一个好的transformation；

那么如何让机器自动产生一个transformation？
解答：把很多个Logistic Regression cascade（级联）起来
假设有两个input：$x_1$、$x_2$，通过一个Logistic Regression的model，；两个input通过这个model相加得到$x_1^{{}^{\prime }}$，同理，通过另一个model得到$x_2^{{}^{\prime }}$，通过这组数据就可以再通过一个Logistic Regression 的model把两类分开，如下图：

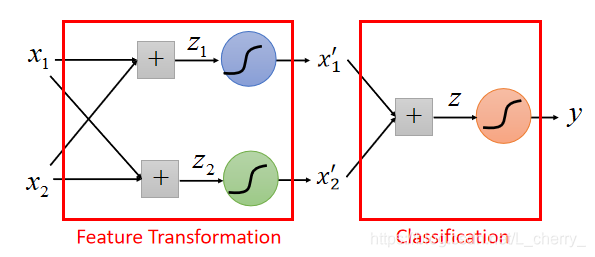
举例：

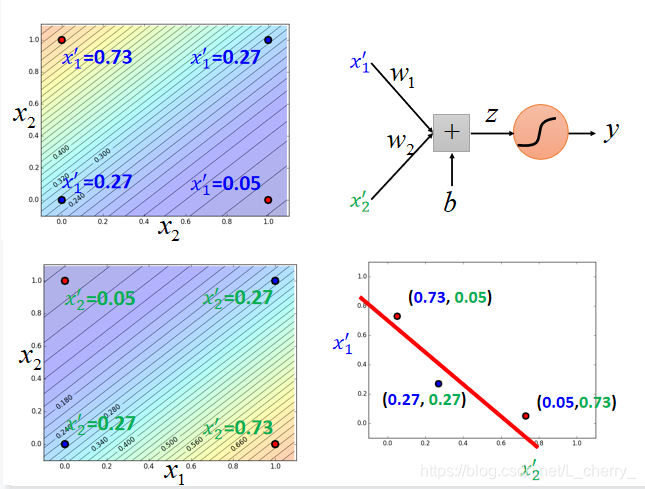
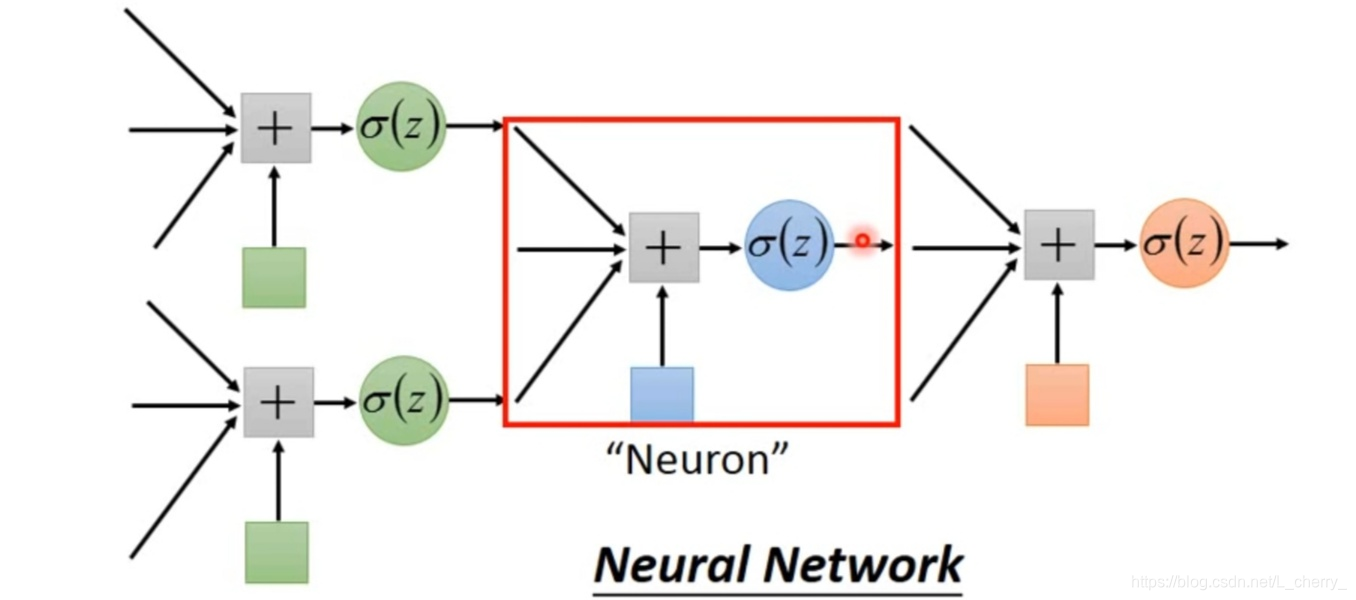
某一个Logistic Regression 的model一部分是来自于其它Logistic Regression 的Output，而某一个Logistic Regression 的Output也可以是其它Logistic Regression 的Input，可以把每一个其它Logistic Regression叫做一个“Neuron”；把这些“Neuron”串起来就叫做“Neural Network‘。

本文是对blibli上李宏毅机器学习2020的总结，如有侵权会立马删除。