1 R 2 R^2 R2计算公式
若用
y
i
y_i
yi?表示真实的观测值,用
y
ˉ
\bar{y}
yˉ?表示真实观测值的平均值,用
y
i
^
\hat{y_i}
yi?^?表示预测值,则
R
2
=
1
?
∑
i
=
1
n
(
y
i
?
y
^
i
)
2
∑
i
=
1
n
(
y
i
?
y
2
)
2
R^{2}=1-\frac{\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{\sum_{i=1}^{n}\left(y_{i}-y^{2}\right)^{2}}
R2=1?∑i=1n?(yi??y2)2∑i=1n?(yi??y^?i?)2?
即
R
2
=
1
?
∑
i
(
y
i
?
y
i
)
2
/
n
∑
i
(
y
i
?
y
^
)
2
/
n
=
1
?
R
M
S
E
Var
?
R^{2}=1-\frac{\sum_{i}\left(y_{i}-y_{i}\right)^{2} / n}{\sum_{i}\left(y_{i}-\hat{y}\right)^{2} / n}=1-\frac{R M S E}{\operatorname{Var}}
R2=1?∑i?(yi??y^?)2/n∑i?(yi??yi?)2/n?=1?VarRMSE?
分子就变成了常用的评价指标均方根误差RMSE,分母就变成了方差Var。
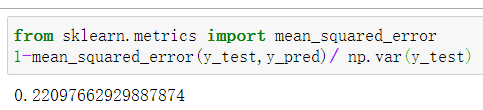
2 利用Python的误差值实现
from sklearn.metrics import mean_squared_error
1-mean_squared_error(y_test,y_pred)/ np.var(y_test)
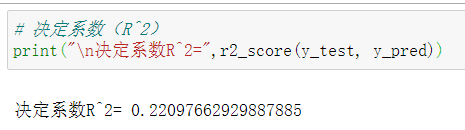
3 利用sklearn.metrics.r2_score实现
from sklearn.metrics import r2_score
print("\n决定系数R^2=",r2_score(y_test, y_pred))
4 笔者认为:
- 决定系数
一般用在回归模型的评价中; - 因为分类模型的预测值只有0,1,在
分类模型中非 0 即 1,这样利用公式计算时对模型的评测结果是不合适的。