讲在前面

一.笔者最近来搞心电信号了，当前算法框架就参考的这篇论文，来钻研一下这篇论文。说真的，搞ecg的人真的太少了；
二.我设计了几种字体颜色用于更加醒目地表现关键的思想和主题：
- 红色表示尚未理解透彻的一些概念
- 蓝色表示对原来的理解做的一些修改或补充
- 绿色表示此处需要参考的论文其他部分
- 橙色表示本文的重要关键字
- 紫色表示后续更新的内容
- ~~我会用删除线将自己曾经不到位的理解进行删除~~

摘要

我们提出了一种类似于UNet的全卷积网络来实现对ECG信号的分割，算法可以输入任意采样率的信号，然后输出一系列P波、T波的起点终点和QRS波群（波群的输出形式？）。我们的方法在速度上和其他算法不同，因为参数很少，同时效果又很好（对采样率有自适应性并且适用于多种ECG监视器）。提出的这个方法在质量上要优于其他的SOTA级别的分割算法。特别要指出的是，F1-measures对P、T波的起点与终点和QRS波群的检测精度都至少在97.8%、99.5%和99.0%。

1. 介绍

ECG是心脏的心电活动记录仪，是通过人身上携带的电极获得的。这是诊断心脏病的最重要的方法。ECG通常是由医生进行诊断，最近ECG信号的自动分析引起了广泛的关注。
ECG信号分析包含P、T、QRS波群的检测，以及各自的形状、幅度、相应位置等的分析（如下图）。
图1：
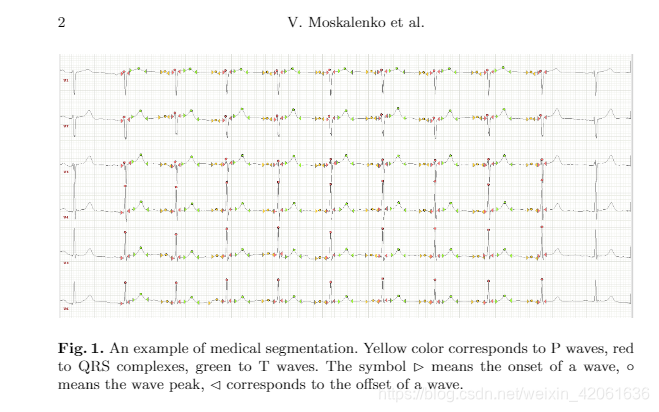
在这里插入图片描述
这三个波的起点和终点检测也被叫做ECG信号分割或者ECG信号勾画。
对ECG进行自动分割因为以下原因而成为一个困难的问题。比如，P波的幅度很小，所以很容易被识别成电极移动或者肌肉噪声产生的一些干涉等等。P波和T波可以是双向的，所以精确判断它的起点和终点就相对有点困难。有些心脏的周期可能不全是标准的分割，比如，P波可能消失等等。
在所有ECG自动分割的方法中，使用wavelet transform已经被证明是最好的方法【3,4,7,6,8,9】，在【11】中，一种ECG分割的神经网络方法被提出，这种算法的效果基本达到了wavelet transform的级别，但是仍然比较低。在这片论文中，我们建议使用UNet结构的神经网络。结果，使用这种神经网络的方法可能达到了，甚至超越了其他分割算法的质量。就质量而言，这种算法已经超过了其他同类算法。特别要指出的是，F1-measures对P、T波的起点与终点和QRS波群的检测精度都至少在97.8%、99.5%和99.0%。
另外要说的是，我们提出的分割算法在速度上与其他算法有所不同，因为它参数量很小，而且具备对于不同采样频率和不同类型设备的自适应性。
下面是论文所提出方法的主要不同点：

【11】提出了一种12个卷积神经网络的合并，这里我们使用的是一个带有跳层连接的全连接网络；
与现在的方法相比，【11】没有使用后处理；
【11】使用预处理来移除等值线偏移，通过这样处理数据，即使有等值线偏移的情况下也能很好的分割信号。这点从Section3.3可以看出来。

2. 算法

2.1 预处理

下面描述的神经网络是在一个采样频率为500Hz、周期为10s的ECG信号上进行训练的（看Section3.1）。为了使得算法能在不同采样频率和不同时长的信号上使用，我们提出了以下的预处理方法，假设输入信号 $x=(x_1,x_2,...,x_n)$ 的频率为 $v$ ，训练集信号频率为 $μ$ 。那么 $T = n / v$ 就是信号的周期。把输入的信号做如下转换：

1.构建一个时间采样点的数组 $t = (t_1, t_2, ...,t_n)$ ，将一个长度为 $[0, T]$ 的信号分成 $n$ 个相等的部分 $(i = 1, 2, . . ., n)$ ， $t_i=(\frac{(2i-1)*T}{2n})$ 就是每段时间间隔的中点。
2.通过点集{ $t_1,x_1),(t_2,x_2),...,(t_n,x_n)$ }，构建cubic spline【2】。
3.组成一个时序数组 $t^{'}=(t_1^{'},t_2^{'},...,t_m^{'})$ ，这里：
$t_i^{'}=\frac{(2i-1)T}{2m}$
4.使用cubic spline，找到 $t^{'}$ 处的信号值，所得到的结果就是神经网络的输入。

2.2 神经网络结构

神经网络结构与UNet结构相似【10】，如图2：
图2：
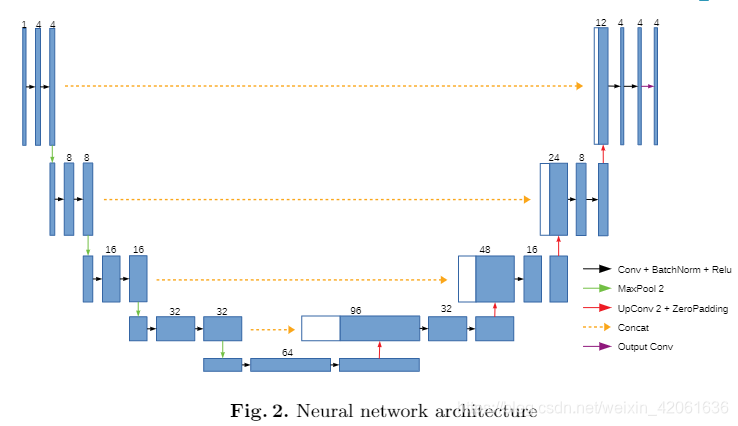
在这里插入图片描述
神经网络的输入是一个长度为 $l$ 的向量， $l$ 是每一条传入的信号的长度，每一条数据独立输入神经网络。
输出的尺寸为 $(4, l)$ ，输出矩阵的每列包含有四个分数，分别表示分割为P、QRS、T或者其他的置信度。提出的网络包含了以下几个层：

(i) 4个block，每个里面包含了两个卷积层+bn+relu，每个block之间通过最大池化层进行连接；
(ii) 上一个block的输出经过最大池化后，作为下一个block的输入；
(iii) 反卷积和0填充后的输出，与对应位置上的层的输出进行concat，输入下一层；
(iv) concat后的输出同样要进行卷积+BN+relu；
(v) 上层卷积的结果是下一层卷积的输入。
所有卷积的kernelsize=9，padding=4，所有反卷积层的kernelsize=8，stride=2，padding=3。每个block的最后的卷积的kernelsize=1。
我们提出的网络和UNet网络有以下不同点：
使用一维卷积代替了二维卷积；
我们在卷积层使用了不同的通道数和不同的参数；
我们使用copy+zero pad layer代替了copy+crop layer，用这种方法，得到的输出的维度和输入的维度相同，而UNet的网络输出是一张图片。

2.3 后处理

神经网络的输出是形状为 $(4, l)$ ， $l$ 是信号的长度。通过对矩阵的每列应用argmax函数，我们得到了一个长度为 $l$ 的方向向量。然后将波的数组组合在一起，找到所有连续的具有相同标签的段。

3 实验结果

3.1 LUDB数据集

神经网络的训练和实验是在扩展的LUDB数据集【5】上进行的。这个数据集包含了455个12导联的ECG（周期为10s，采样频率为500Hz）。为了对算法进行比较，数据集被分成了训练集和测试集，测试集包含了200个从原始LUDB数据集中拿来的ECG。由于我们提出的方法独立处理每一个导联，所以训练时实际使用了255x12=3060个长度为500x10=5000的信号。为了避免过拟合，我们使用了数据增强的方法：在每一个batch的迭代过程中，一个4s的随机连续的ECG分段被输入到神经网络。
LUDB数据集有以下几个特征：前一个（或者前两个）和最后一个心脏周期并没有标注。同时，第一个和最后一个标注的分段一定时QRS（看下图一）。为了和对应的分割结果进行一个正确的对比，算法使用了下面的修改方式：

1.在数据增强的过程中，前两秒和后两秒的数据不使用，比如：长度为4s的子序列是从第2秒到第4秒开始（从第6秒到第8s结束）；
2.为了避免假阳性，第一个和最后一个心脏周期在算法验证时被移除。

3.2 算法比较

表一包含了实验结果，以及和使用wavelet的算法【4】、使用其他神经网络分割算法【11】的对比。最后一行展示了我们的算法对包含200x12=2400个ECG信号，独立分析每一个导联的特征。
表一：
在这里插入图片描述
我们通过下列步骤确定算法的质量。根据医疗器械协会的建议，如果机器计算的结果与医生标注的位置的偏差在150ms以内则认为是标注正确。
如果算法正确检测到了一个有意义的点（比如P、QRS、T波的起点或者终点），那么一个真阳性 $(T P)$ 指标将会被计数，同时会自动测量和医生标注位置的偏差。如果在医生标注的位置附近正负某个范围内没有找到这个有意义的点，那么 $I$ 类型错误就会被计数，也就是指假阳性 $(F P)$ 。如果算法没有检测到任何有意义的点，那么 $I I$ 类型错误将会被计数，也就是指 $(F N)$ 。
根据【3，6，8，9】，我们进行了下面质量算法的测量：

1.平均误差 $m$ ；
2.平均误差的标准差 $\sigma$ ;
3.敏感/回归率， $S e = T P / (T P + F P)$
4.阳性预测值/精确率， $P P V = T P / (T P + F P)$

这里TP、FP、FN分别表示的是标记正确的数量、类型 $I$ 错误，类型 $I I$ 错误。我们也给出了 $F 1 ? m e a s u r e$ 的值： $F1=2\frac{Se*PPV}{Se+PPV}$

通过分析表一的结果，我们能够得出以下结论：

1.我们提出的算法的 $S e$ 和 $P P V$ 的指标，在所有分割算法中几乎是最高的；
2.averaging the answer over all 12 leads helps to detect the complexes better:it has improved both Se and PPV; however, the detecting the onsets and the offsets worsens, which is indicated by the growth of σ in all indicators；
3.如果想要检测qrs波群的话，只用II导联就行了，这样会减少12倍的时间，不用把其他导联送入神经网络；
4.算法给出了最好的 $\sigma$ 【4】
5.算法表现超过了其他的神经网络方法【11】。

3.3 一些分割的例子

我们所提出算法的分割例子在图3至图7中显示：
实验表明我们的算法能够处理不同频率的噪声干扰，图三是低频率的噪声干扰（呼吸），图四是高频率的噪声干扰。
图三：
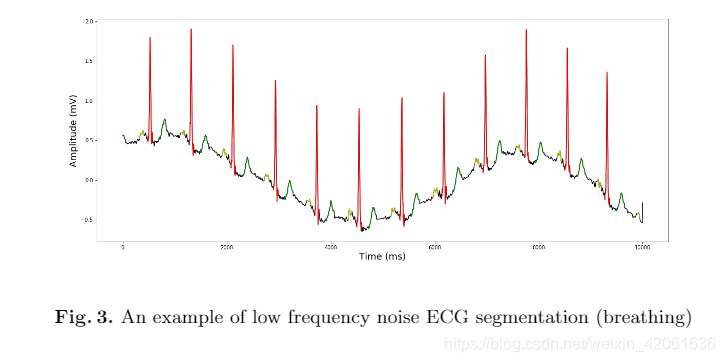
在这里插入图片描述
图四：

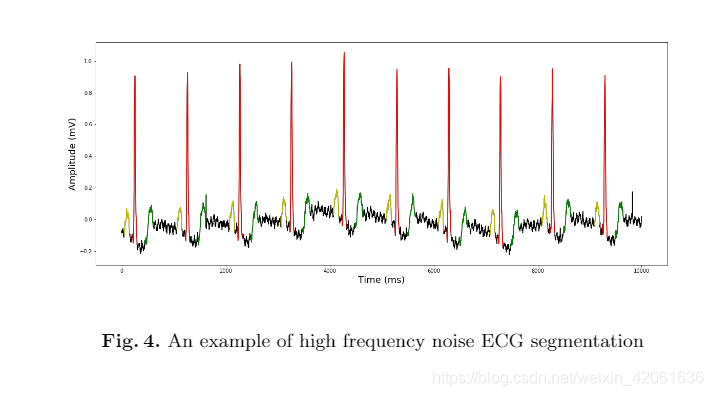
图五是一个心室早搏（ventricular extrasystole）患者的ECG信号：
图五：

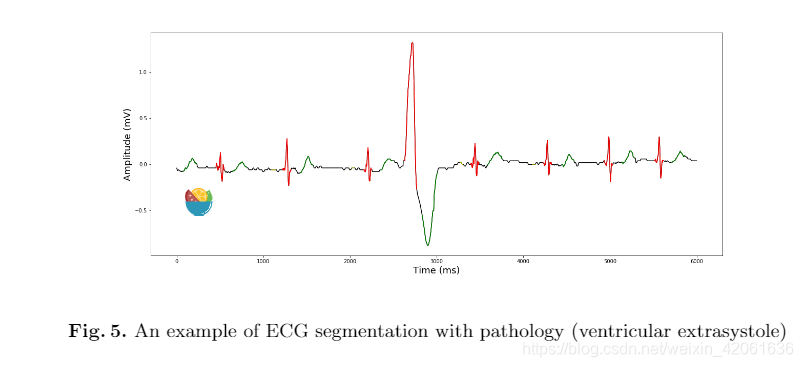
图六是来自于另一种类型ECG检测仪的信号，这个信号的T波很高，而且信号更平滑：
图六：

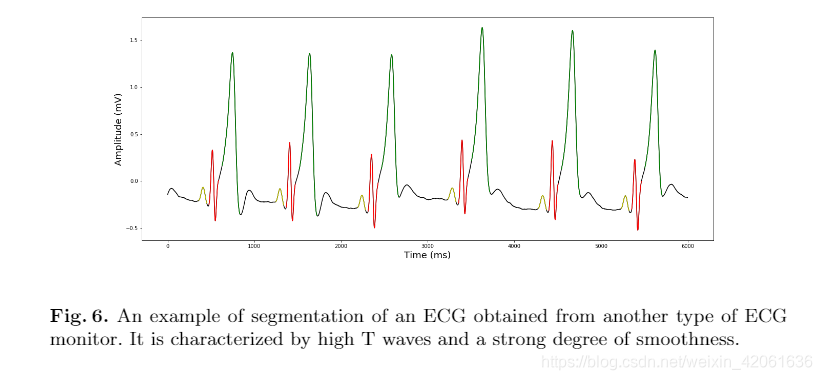
图七显示的是一个采样频率为50HZ的ECG信号，通过cubic spline插值到500HZ的分割结果：
图七：
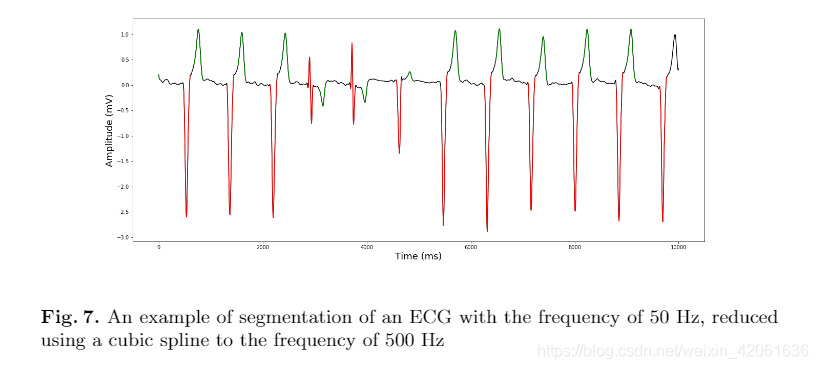
在这里插入图片描述

4 总结和未来工作

这篇论文是建立在UNet网络结构之上的，事实证明可以很好的用来分割ECG信号。我们的算法虽然参数量很少，但是生成效果很好。尤其对于不同的采样率和不同类型的检测器。该算法的质量由于其他算法，P、T、QRS的 $F 1 ? m e a s u r e$ 指标至少都为99.5%、99.9%、99.9%。
这个算法在未来可能会用于诊断目的，使用这个分割算法可以将分割的结果输入到其他的神经网络，从而提升分类的准确率。
另外，有一个可能对算法性能有改善的方法。尤其，这个算法种所提出的损失函数可能并不会真正影响分割的质量。比如它并没有考虑ECG的一些特征。（比如两个QRS波群并不会过于近，或者过于远）。