[人工智能]PyTorch实现前馈神经网络（手动）

回归任务

该回归问题为高维回归问题，涉及的自变量过多，因此不适合用之前的线性回归模型，因为模型过于简单容易导致训练的效率太低。因此我们考虑利用前馈神经网络，增加隐藏层，并且为了避免梯度消失问题，在隐藏层采用relu激活函数。

导入包

import torch
import numpy as np
import random
from IPython import display
import torch.utils.data as Data

自定义数据集

num_inputs = 500
num_examples = 10000
#
true_w = torch.ones(500,1)*0.0056
true_b = 0.028
#随机生成的数据样本
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)#行*列=10000*500
labels = torch.mm(features,true_w) + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float) #扰动项
#训练集和测试集上的样本&标签数----真实的特征和样本
trainfeatures = features[:7000]
trainlabels = labels[:7000]
testfeatures = features[7000:]  
testlabels = labels[7000:]
print(trainfeatures.shape,trainlabels.shape,testfeatures.shape,testlabels.shape)

torch.Size([7000, 500]) torch.Size([7000, 1]) torch.Size([3000, 500]) torch.Size([3000, 1])

构造数据迭代器

采用torch.utils.data.DataLoader读取小批量数据，分别定义关于训练集数据和测试集数据的迭代器iterate

• batch_size是超参数，表示一轮放入多少个样本进行训练
• shuffle是否打乱数据，True表示打乱数据
• num_workers=0表示不开启多线程读取数据

注：利用Data.TensorDataset获取数据集，Data.DataLoader构建数据迭代器，从而实现数据的批量读取。

#获得数据迭代器
batch_size = 50 # 设置小批量大小
def load_array(data_arrays, batch_size, is_train=True):  #自定义函数
    """构造一个PyTorch数据迭代器。"""
    dataset = Data.TensorDataset(*data_arrays)#features 和 labels作为list传入，得到PyTorch的一个数据集
    return Data.DataLoader(dataset, batch_size, shuffle=is_train,num_workers=0)#返回的是实例化后的DataLoader
train_iter = load_array([trainfeatures,trainlabels],batch_size)
test_iter = load_array([testfeatures,testlabels],batch_size)

# 测试:利用python内置函数next，从迭代器中获取第一项。
next(iter(train_iter))

初始化参数

初始化参数针对神经网络相关数据：

• 宏观层面(超参数)：输入层、隐藏层、输出层的维度，分别为：num_inputs/num_hiddens/num_outputs；
• 微观层面：W1,b1,W2,b2

注：如果从A–>B，则W.shape = (A * B),这样可以直接参与mm，不用转置.t()

由于XW1 + b1结构：X.shape=(num_example * num_input) 因此W1.shape=(num_inputs * num_hiddens)
XW1结果为：num_example * num_hiddens作为隐藏层的输入

#定义超参数
num_inputs=500
num_hiddens = 256
num_outputs = 1
#定义参数
W1 = torch.tensor(np.random.normal(0, 0.01, (num_inputs,num_hiddens)), dtype=torch.float32)  
b1 = torch.zeros(1, dtype=torch.float32)  
W2 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens,num_outputs)), dtype=torch.float32)  
b2 = torch.zeros(1, dtype=torch.float32)  
params = [W1,b1,W2,b2]
for param in params:
    param.requires_grad_(requires_grad = True)#设置为true，追踪并记录所有在计算图上的操作（正向积累）

定义隐藏层激活函数

对隐藏层通常使用Relu激活函数，当x>0时，不存在梯度消失问题

def relu(x):
    x=torch.max(x,torch.tensor(0.0))
    return x
#     a = torch.zeros_like(x)#与X.shape一致的零张量
#     return torch.max(x,a)#即X>0.输出为X,否则输出为0
x =torch.tensor(2)
relu(x),relu(-x)

定义模型

#定义模型  
def net(X):  
    X = X.view((-1,num_inputs)) #将数据进行展平，对于空间结构的数据生效
    H = relu(torch.matmul(X,W1)+b1)  
    return torch.matmul(H,W2)+b2  

#测试 @可以表示矩阵乘法
a=torch.ones(2,3)
b = torch.ones(3,4)
a@b,(a@b).size()

损失函数

由于是回归问题，因此使用torch模块自带的最小化均方误差。对于回归问题，损失是唯一的衡量标准，对于分类问题，一般采取更直观的角度进行衡量模型的效果，即分类的准确率。

loss = torch.nn.MSELoss()

优化算法

小批量随机梯度下降:

在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。接下来，朝着减少损失的方向更新我们的参数。 下面的函数实现小批量随机梯度下降更新。该函数接受模型参数集合、学习速率和批量大小作为输入。每一步更新的大小由学习速率lr决定。

理解下面这句话：
因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size）来归一化步长，这样步长大小就不会取决于我们对批量大小的选择。（步长即?param.data，param.grad与批量样本的大小有关，因此需要归一化）

def SGD (params,lr,batch_size):
    for param in params:
        param.data -= lr * param.grad/batch_size

训练

定义训练函数

对于每一轮次的训练;

• step1:在训练集上，进行小批量梯度下降更新参数
• step2 每经过一个轮次的训练， 记录训练集和测试集上的loss

#记录列表（list），存储训练集和测试集上经过每一轮次，loss的变化
def train (net,train_iter,test_iter,loss,num_epochs,batch_size,params = None,lr=None,optimizer=None):
    train_loss=[]
    test_loss=[]
    for epoch in range(num_epochs):#外循环控制循环轮次
        #step1在训练集上，进行小批量梯度下降更新参数
        for X,y in train_iter:#内循环控制训练批次
            y_hat = net(X)
            l = loss(y_hat,y)#l.size = torch.Size([]),即说明loss为表示*标量*的tensor`
            #梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            l.backward()
            if optimizer is None:
                SGD(params,lr,batch_size)
            else:
                optimizer.step()
        #step2 每经过一个轮次的训练， 记录训练集和测试集上的loss
        train_labels = trainlabels.view(-1,1)  
        test_labels = testlabels.view(-1,1) 
        train_loss.append((loss(net(trainfeatures),train_labels)).item())#！注意要取平均值
        test_loss.append((loss(net(testfeatures),test_labels)).item())
        print("epoch %d,train_loss %.6f,test_loss %.6f"%(epoch+1,train_loss[epoch],test_loss[epoch])) 
    return train_loss, test_loss

开始训练模型

lr=0.01
num_epochs = 100
#batch_size、params epc已经定义
train_loss, test_loss = train (net,train_iter,test_iter,loss,num_epochs,batch_size,params,lr)#每一给optimizer,默认None

epoch 1,train_loss 0.016171,test_loss 0.016306
epoch 2,train_loss 0.016082,test_loss 0.016221
epoch 3,train_loss 0.016013,test_loss 0.016155
epoch 4,train_loss 0.015956,test_loss 0.016101
epoch 5,train_loss 0.015908,test_loss 0.016056
epoch 6,train_loss 0.015867,test_loss 0.016018
epoch 7,train_loss 0.015831,test_loss 0.015985
epoch 8,train_loss 0.015798,test_loss 0.015956
epoch 9,train_loss 0.015768,test_loss 0.015929
epoch 10,train_loss 0.015739,test_loss 0.015903
epoch 11,train_loss 0.015712,test_loss 0.015879
......
epoch 93,train_loss 0.013922,test_loss 0.014301
epoch 94,train_loss 0.013901,test_loss 0.014283
epoch 95,train_loss 0.013880,test_loss 0.014264
epoch 96,train_loss 0.013858,test_loss 0.014245
epoch 97,train_loss 0.013837,test_loss 0.014227
epoch 98,train_loss 0.013816,test_loss 0.014208
epoch 99,train_loss 0.013795,test_loss 0.014189
epoch 100,train_loss 0.013773,test_loss 0.014170

绘制loss曲线

import matplotlib.pyplot as plt
x=np.linspace(0,len(train_loss),len(train_loss))
plt.plot(x,train_loss,label="train_loss",linewidth=1.5)
plt.plot(x,test_loss,label="test_loss",linewidth=1.5)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.legend()
plt.show()

?

二分类任务

#在执行一个新的任务之前，先将之前的中间变量的结果全部清空，即之前的编译不作数
%reset

Once deleted, variables cannot be recovered. Proceed (y/[n])? y

导入所需要的包

import torch
import numpy as np
import random
from IPython import display
import torch.utils.data as Data

自定义数据集

共生成两个数据集。

• 两个数据集的大小均为10000且训练集大小为7000，测试集大小为3000。
• 两个数据集的样本特征x的维度均为200，且分别服从均值互为相反数且方差相同的正态分布。
• 两个数据集的样本标签分别为0和1。

然后利用torch.cat()操作将两类的训练集和测试集分别合并，从而训练集的大小为14000，测试集的大小为6000。

num_inputs = 200
#1类
x1 = torch.normal(2,1,(10000,num_inputs))
y1 = torch.ones(10000,1)#标签1
x1_train = x1[:7000]
x1_test = x1[7000:]
#0类
x2 = torch.normal(-2,1,(10000,num_inputs))
y2 = torch.zeros(10000,1)#标签1
x2_train = x1[:7000]
x2_test = x1[7000:]
#合并数据----按行合并，即dim=0，且分训练集和测试集
    ##合并训练集数据（包括特征和标签）
trainfeatures=torch.cat((x1_train,x2_train),0).type(torch.FloatTensor)
trainlabels = torch.cat((y1[:7000],y2[:7000]),0).type(torch.FloatTensor)
    ##合并测试集数据
testfeatures=torch.cat((x1_test,x2_test),0).type(torch.FloatTensor)
testlabels=torch.cat((y1[7000:],y2[7000:]),0).type(torch.FloatTensor)
print(trainfeatures.shape,trainlabels.shape,testfeatures.shape,testlabels.shape)

torch.Size([14000, 200]) torch.Size([14000, 1]) torch.Size([6000, 200]) torch.Size([6000, 1])

构造数据迭代器

#设置批量大小
batch_size = 50
'''构造训练数据迭代器'''
#将训练数据的特征和标签组合---形成训练数据集
dataset1 = Data.TensorDataset(trainfeatures,trainlabels)
train_iter = Data.DataLoader(
    dataset=dataset1,#torch TensorDataset format
    batch_size = batch_size,#mini batch size
    shuffle =True,#是否打乱数据（训练集一般需要打乱）
    num_workers=0,#多线程读取数据，注意在windows下需要设置为0
)
'''构造测试数据迭代器'''
dataset2 = Data.TensorDataset(testfeatures,testlabels)
test_iter = Data.DataLoader(
    dataset = dataset2,
    batch_size = batch_size,
    shuffle = False,#测试集一般不需要打乱
    num_workers=0,
)

初始化参数

这部分和回归部分大致一样，因为网络的大体模型（如：隐藏层、隐藏单元的个数、以及最后的输出层神经元个数）是一样的，只是输入层的特征不同而已

#定义超参数
# num_inputs=200
num_hiddens = 100
num_outputs = 1
#定义参数
#参数初始化时，将参数的方差调大，增加不稳定性，方式初始参数刚好与理想参数接近的情况，可以更好的观察模型训练的效果。
W1 = torch.tensor(np.random.normal(0, 1, (num_inputs,num_hiddens)), dtype=torch.float32)  
b1 = torch.zeros(1, dtype=torch.float32)#wx+b时，会调用广播算法  
W2 = torch.tensor(np.random.normal(0, 1, (num_hiddens,num_outputs)), dtype=torch.float32)  
b2 = torch.zeros(1, dtype=torch.float32)  
params = [W1,b1,W2,b2]
for param in params:
    param.requires_grad_(requires_grad = True)#设置为true，追踪并记录所有在计算图上的操作（正向积累）

定义隐藏层激活函数

def relu(x):
    x=torch.max(x,torch.tensor(0.0))
    return x

定义模型

经过隐层，得到的tensor的size是num_example * num_hiddens，每一行代表每一个样本的在num_hiddens个神经元上的输出。
激活是，通过relu函数，若得到的tensor元素小于0的，则用0代替。

def net (X):
    X=X.view((-1,num_inputs))
    H=relu(torch.mm(X,W1)+b1)
    return torch.mm(H,W2)+b2 

损失函数

对于输出单元，由于是二分类问题，我们采用Sigmoid单元，常用于输出伯努利分布，适合二分类问题。
作为输出层的Sigmoid激活函数，这里我利用torch.nn.BCEWithLogitsLoss()函数，它将Sigmoid函数和交叉熵损失函数合并在了一起计算，相比于单独计算更加稳定了，然后同样是小批量随机梯度下降法进行梯度更新。

# 定义二分类交叉熵损失函数
loss = torch.nn.BCEWithLogitsLoss()

优化算法

同样是小批量随机梯度下降法进行梯度更新

def SGD (params,lr,batch_size):
    for param in params:
        param.data -= lr * param.grad/batch_size

训练

定义训练函数

#记录列表（list），存储训练集和测试集上经过每一轮次，loss的变化
def train (net,train_iter,test_iter,loss,num_epochs,batch_size,params = None,lr=None,optimizer=None):
    train_loss=[]
    test_loss=[]
    for epoch in range(num_epochs):#外循环控制循环轮次
        train_l_sum=0.0#记录训练集上的损失
        test_l_sum=0.0
        n =0.0
        #step1在训练集上，进行小批量梯度下降更新参数
        for X,y in train_iter:#内循环控制训练批次
            y_hat = net(X)
            #保证y与y_hat维度一致，否则将会发生广播
            l = loss(y_hat,y.view(-1,1))#这里计算出的loss是已经求过平均的，l.size = torch.Size([]),即说明loss为表示*标量*的tensor`
            #梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            l.backward()
            if optimizer is None:
                SGD(params,lr,batch_size)
            else:
                optimizer.step()
#             #计算每个epoch的loss
#             train_l_sum += l.item()
#             n+=y.shape[0]
        #step2 每经过一个轮次的训练， 记录训练集和测试集上的loss
        #注意要取平均值，loss已经默认求了平均值，因此我们不用再老费苦心，直接apply在测试集和训练集上。
        test_l_sum = loss(net(testfeatures),testlabels).item()
        train_l_sum = loss(net(trainfeatures),trainlabels).item()
        train_loss.append(train_l_sum)
        test_loss.append(test_l_sum)
        print("epoch %d,train_loss %.6f,test_loss %.6f"%(epoch+1,train_loss[epoch],test_loss[epoch])) 
    return train_loss, test_loss

开始训练模型

注：为什么重复运行train函数时，结果不一样，往往是第一次的结果较为合理。因为运行完一次train中，params已经更新，第二次运行时，计算得到的误差就会非常小！
因此，每次执行train之前，务必重新进行一次参数的初始化。

lr = 0.01
num_epochs = 100
train_loss,test_loss = train(net,train_iter,test_iter,loss,num_epochs,batch_size,params,lr)

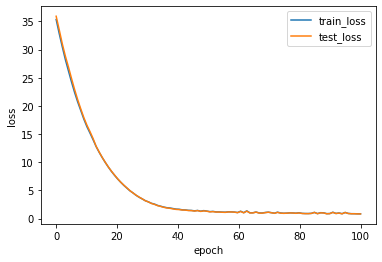
epoch 1,train_loss 35.329754,test_loss 35.914192
epoch 2,train_loss 32.825573,test_loss 33.488113
epoch 3,train_loss 30.459223,test_loss 30.997768
epoch 4,train_loss 28.204462,test_loss 28.817091
......
epoch 94,train_loss 0.874999,test_loss 0.855477
epoch 95,train_loss 1.093810,test_loss 1.089528
epoch 96,train_loss 0.925214,test_loss 0.902054
epoch 97,train_loss 0.876389,test_loss 0.864307
epoch 98,train_loss 0.873619,test_loss 0.862228
epoch 99,train_loss 0.854139,test_loss 0.836681
epoch 100,train_loss 0.850759,test_loss 0.834266

绘制loss曲线

import matplotlib.pyplot as plt
x=np.linspace(0,len(train_loss),len(train_loss))
plt.plot(x,train_loss,label="train_loss",linewidth=1.5)
plt.plot(x,test_loss,label="test_loss",linewidth=1.5)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.legend()
plt.show()

?

多分类任务

#在执行一个新的任务之前，先将之前的中间变量的结果全部清空，即之前的编译不作数
%reset

Once deleted, variables cannot be recovered. Proceed (y/[n])? y

导入包

import torch
import numpy as np
import random
from IPython import display
import torch.utils.data as Data
import torchvision
import torchvision.transforms as transforms

下载MNIST数据集

按实验要求，这里利用torchvision模块下载了数字手写数据集:

• 其中训练集为60000张图片，测试集为10000张图片，其每个图片对应的标签是0-9之间，分别代表手写数字0,1,2,3,4,5,6,7,8,9.
• 图像是固定大小(28x28像素)，其值为0到1。为每个图像都被平展并转换为784(28 * 28)个特征的一维numpy数组。

#下载MNIST手写数据集 :包括训练集和测试集
train_dataset = torchvision.datasets.MNIST(root='./Datasets/MNIST', train=True,  download=True, transform=transforms.ToTensor())  
test_dataset = torchvision.datasets.MNIST(root='./Datasets/MNIST', train=False,  download=True, transform=transforms.ToTensor())  

定义数据迭代器

通过测试，输出X.shape为torch.Size([32, 1, 28, 28]) ：

• 32个图像
• 1代表图像为黑白，只有一个通道
• 28*28为图像的大小

torch.Size([32])，则代表32个图像，每个图像有一个对应的标签

batch_size = 32  
train_iter = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True,  num_workers=0)  
test_iter = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=False,  num_workers=0) 
#测试：
for X, y in train_iter:
    print(X.shape,y.shape)
    break

torch.Size([32, 1, 28, 28]) torch.Size([32])

初始化参数

#超参数初始化
num_inputs=784 #28*28
num_hiddens=256
num_outputs=10
#参数初始化
W1 = torch.tensor(np.random.normal(0,0.01,(num_inputs,num_hiddens)),dtype=torch.float32)
b1 = torch.zeros(1,dtype=torch.float32)
W2 = torch.tensor(np.random.normal(0,0.01,(num_hiddens,num_outputs)),dtype=torch.float32)
b2 = torch.zeros(1,dtype=torch.float32)
params = [W1,b2,W2,b2]
for param in params:
    param.requires_grad_(requires_grad = True)

定义隐藏层的激活函数

#x为矩阵tensor
##对于一个小批量样本的训练而言，X=32*784，W=784*256，得到的relu函数参数：32*256
##表示32个样本，每个样本在256个隐藏层神经元上的输出值
def relu(x):
    x = torch.max(x,torch.tensor(0.0))
    return x

定义模型

def net (X):
    #因为我们忽略了空间结构，所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量。
    X = X.reshape((-1,num_inputs))#X.shape为torch.Size([32, 1, 28, 28]) 展平为32*728
    H = relu(X@W1+b1)
    return (H@W2+b2)#所得结果shape为32*10,代表32个样本,分别在10个输出层神经元上的输出。

#测试矩阵乘法
# for X, y in train_iter:
#     X = X.reshape((-1,num_inputs))
#     print(X.shape,W1.shape)
#     print(torch.mm(X,W1)==X@W1)#证明可以用@代替矩阵乘法
#     break

定义交叉熵损失函数

作为输出层的Softmax激活函数，这里我利用torch.nn. CrossEntropyLoss（）函数，它将Softmax函数和交叉熵损失函数合并在了一起计算，同理相比于单独计算更加稳定了。
这也解释了为什么输出层没用Softmax激活的原因，因为在这里做了激活。可以尝试理解为，在loss类的实例化的过程中，在CrossEntropyLoss的构造函数中完成了对输出层的softmax激活

loss = torch.nn.CrossEntropyLoss()

定义优化器

def SGD(paras,lr,batch_size):  
    for param in params:  
        param.data -= lr * param.grad/batch_size

定义准确率检验器

加入了对测试集的准确率的判断，利用测试集的预测值和真实值进行比较，计算测试准确的概率。
FUN
其中y_hat.argmax(dim=1)返回矩阵y_hat每行中最大元素的索引，且返回结果与变量y形状相同。相等条件判断式(y_hat.argmax(dim=1) == y)是一个类型为ByteTensor的Tensor,即tensor.bool，我们用float()将其转换为值为0（相等为假）或1（相等为真）的浮点型Tensor,即tensor.float。或者通过sum()直接转为为torch.int类型，再通item转换为int类型。

对于本次的检验器，给定一个数据迭代器，两个功能：

• 计算准确率
• 计算loss

#返回准确率以及loss
flag=0
def evaluate_accuracy_loss(net, data_iter):
    acc_sum=0.0
    loss_sum=0.0
    n=0
    global flag
    for X,y in data_iter:
        y_hat = net(X)
        #if flag==0:print (y_hat)#测试一下y_hat是否已经softmax激活
        #flag = 1
        acc_sum += (y_hat.argmax(dim=1)==y).sum().item()
        l = loss(y_hat,y)
        loss_sum += l.item()*y.shape[0]#由于loss(y_hat,y)默认为求平均，因此*y.shape[0]意味着求和。
        n+=y.shape[0]
    return acc_sum/n,loss_sum/n

训练

定义训练函数

#记录列表（list），存储训练集和测试集上经过每一轮次，loss的变化
def train (net,train_iter,test_iter,loss,num_epochs,batch_size,params = None,lr=None,optimizer=None):
    train_loss=[]
    test_loss=[]
    for epoch in range(num_epochs):#外循环控制循环轮次---跑完一轮，也就把数据走了一遍
        train_l_sum=0.0#记录训练集上的损失
        train_acc_num=0.0#记录训练集上的准确数
        n =0.0
        #step1在训练集上，进行小批量梯度下降更新参数
        for X,y in train_iter:#内循环控制训练批次
            y_hat = net(X)
            #保证y与y_hat维度一致，否则将会发生广播
            l = loss(y_hat,y)#这里计算出的loss是已经求和过的，l.size = torch.Size([]),即说明loss为表示*标量*的tensor`
            #梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            l.backward()
            if optimizer is None:
                SGD(params,lr,batch_size)
            else:
                optimizer.step()
            #每一个迭代周期中得到的训练集上的loss累积进来
            train_l_sum += l.item()*y.shape[0]
            #计算训练样本的准确率---将每个迭代周期中预测正确的样本数累积进来
            train_acc_num += (y_hat.argmax(dim=1)==y).sum().item()#转为int类型
            n += y.shape[0]
        #step2 每经过一个轮次的训练， 记录训练集和测试集上的loss
        #注意要取平均值，loss默认求了sum
        train_loss.append(train_l_sum/n)#训练集loss
        test_acc,test_l = evaluate_accuracy_loss(net,test_iter)
        test_loss.append(test_l)
        print("epoch %d,train_loss %.6f,test_loss %.6f,train_acc %.6f,test_acc %.6f"%(epoch+1,train_loss[epoch],test_loss[epoch],train_acc_num/n,test_acc)) 
    return train_loss, test_loss

开始训练模型

lr = 0.01
num_epochs=20
train_loss,test_loss=train(net,train_iter,test_iter,loss,num_epochs,batch_size,params,lr)

epoch 1,train_loss 2.282583,test_loss 2.272943,train_acc 0.499583,test_acc 0.581100
epoch 2,train_loss 2.261799,test_loss 2.247105,train_acc 0.598233,test_acc 0.614800
epoch 3,train_loss 2.230268,test_loss 2.207617,train_acc 0.608217,test_acc 0.608500
epoch 4,train_loss 2.182300,test_loss 2.148113,train_acc 0.604033,test_acc 0.812700
......
epoch 17,train_loss 0.801846,test_loss 0.759681,train_acc 0.812983,test_acc 0.819800
epoch 18,train_loss 0.759551,test_loss 0.720487,train_acc 0.819817,test_acc 0.826000
epoch 19,train_loss 0.723086,test_loss 0.686695,train_acc 0.825800,test_acc 0.833600
epoch 20,train_loss 0.691361,test_loss 0.657030,train_acc 0.831600,test_acc 0.840300

绘制loss、acc曲线

import matplotlib.pyplot as plt
x=np.linspace(0,len(train_loss),len(train_loss))
plt.plot(x,train_loss,label="train_loss",linewidth=1.5)
plt.plot(x,test_loss,label="test_loss",linewidth=1.5)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.legend()
plt.show()

Reference

https://blog.csdn.net/qq_37534947/article/details/109394648