创建和训练神经网络包括以下基本步骤: ?
- 定义网络结构??
- 使用输入数据在网络上正向传播--forward()
- 计算loss
- 反向传播以计算每个权重的梯度--backward(),计算出的梯度会存在每一个参数的tensor内部
- 使用学习率更新权重--optimizer.step()
第1,2,3步都已经了解,这里记录一下第4步的原理和pytorch中的实现,方便回忆。
原理
反向传播其实就是链式求导法则的另一个名字。在训练时,用给定的输入计算出输出,然后和标准比较计算出loss。然后用loss对每一个参数求偏导。因为用的是梯度下降法,所以是把当前的偏导值乘以学习率更新参数。如果只是一个简单的复合函数f(g(x)),链式法则很容易。但在神经网络中一般会用到多元复合函数求导法则(比如ResNet中的残差链接,就是y=x+f(x))。对于多变量的链式法则如下所示,其中z?=?f(x,?y),其中x?=?g(t),y?=?h(t)。

考虑一个简单的例子,如下图所示:
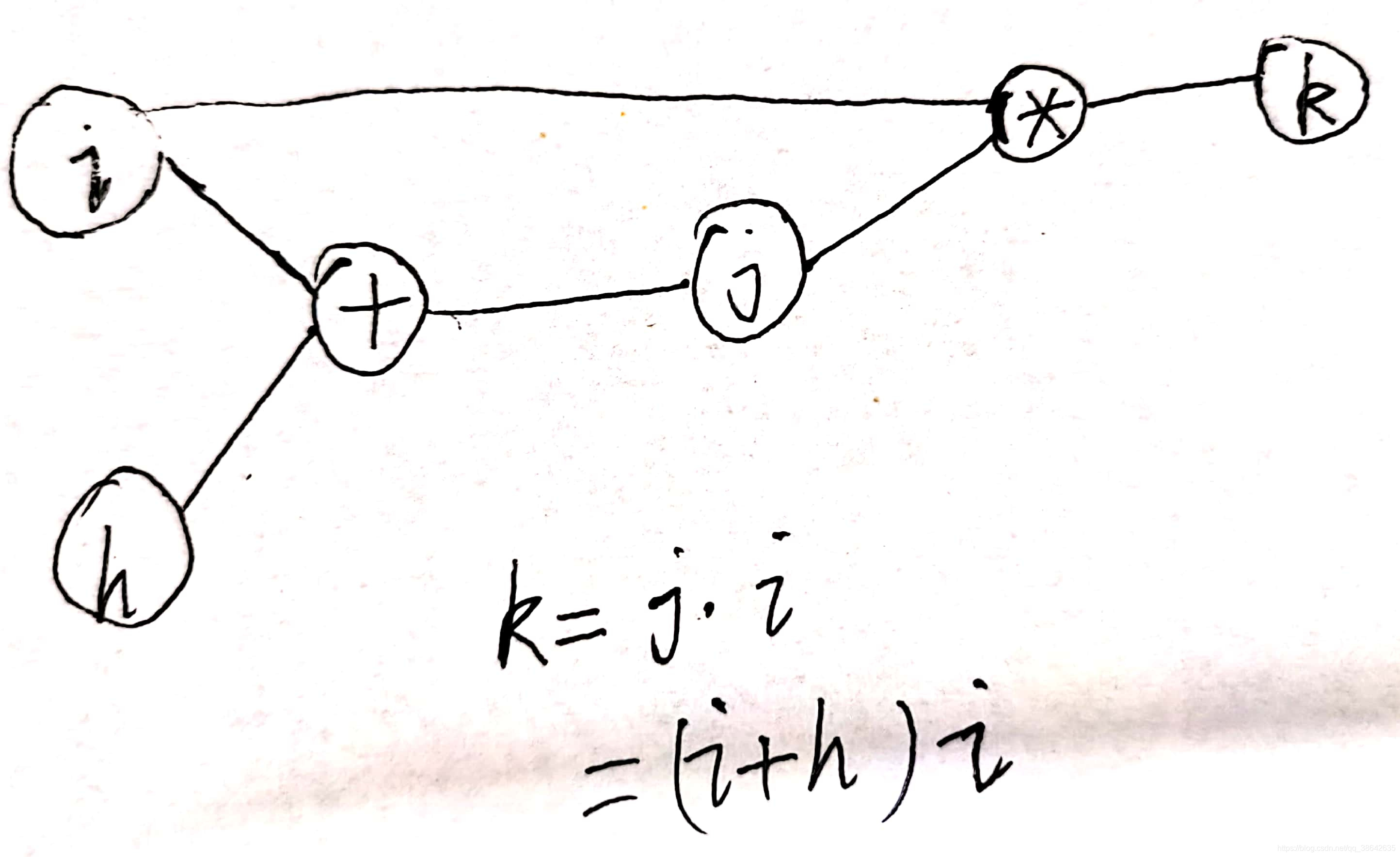
可以看成是残差链接的一个简化版。假如希望求k关于i的偏导,利用链式法则

可以求得k对于i的偏导。这个结果和用k=(i+h)*i求偏导是一样的。但是这种求法可以将求某个变量 的偏导限制在一个局部,方便程序执行。有一个注意的地方就是,在上边的计算图中,i的导数来自两个地方,一个是直接k对i求的,一个是k先对j求,再对i求。这两部分是直接加起来的关系,这是因为多变量的链式法则,对不同部分的偏导就是相加的关系。
pytorch实现
pytorch的实现可以参考这个视频,有一个很好的动画图示,上边的例子也是用的这个视频片尾的例子。
在正向时,除了做正向的计算,pytorch还会自动生成一个叫做计算图的东西。计算图会记录下来每个参数以及他们计算的op。然后在反向传播的时候,就会根据这个计算图来做。为了实现这个功能,tensor除了要存原本的参数外,还需要存额外的数据:
- data:参数本身。
- grad:调用backward()后,计算的梯度。
- grad_fn:这个数据是经过什么运算得到的,反向传播时就会用这个运算的求导。比如k=i*j,k的tensor中grad_fn就是MulBackward。
- is_leaf:是否是叶节点,反向传播会停在叶节点。一般由用户直接创建的tensor是叶节点,require_grad=False的节点是叶节点,使用过detach()的数据也是叶节点。
- require_grad:这个数据是否需要计算梯度。
在使用中,假如一波操作后,最终的输出是一个标量的变量loss。只需要对loss调用.backward(gradient),就可以按照计算图,把loss对每个变量的梯度求出来存在对应的变量中。然后使用optimizer.step(),就可以按照optimizer中定义的learning rate等更新参数。
backward()中的参数gradient需要解释一下。回看之前的例子,如果是k经过j再对i求偏导,那么就是。可以看到,在反向到中间步骤j那里时,计算j对i的偏导时,之前的偏导都已经变成了一个系数,代入j的值后就是个固定值。那么对于一开始的
,也可以有一个人为加入的系数,也就是在backward()中传入的gradient。如果最终的loss就是一个标量,那传入1就可以了。如果是一个向量,就需要传入一个相同长度的单位1向量。在pytorch中,如果最后的loss是一个向量,pytorch会先计算L = torch.sum(loss*gradient),然后再从L开始算梯度。这个操作不影响最终的计算结果。
参考:
https://pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html
https://zhuanlan.zhihu.com/p/29904755