写在前面
我新开了一个系列的文章,主要是有个原因,1:神经网络的结构发生了较大的变化,2:系列文章的更新方式我也有了新的想法。
那么在这个系列里面我就打算以MNIST为例实现基础以及当下流行的神经网络模型,而且文章的结构上,首先我会解决昨天的未解决的问题,接着放出今天的进展,最后再给出第二天亟待解决的问题。
那么今天这篇文章中我主要分享最新的神经网络结构以及正向传递,权重和阈值公式的推导结果。
昨天的问题
1:首先是第一个隐层输出的变化很小的问题,经过今天的分析,我认为很有可能是sigmoid(x)发生了梯度消失,因此我觉得将神经网络的隐层传输函数变成ReLU,输出层的传输函数使用sigmoid(x)。
2:权重,阈值的初始化值对于模型输出的影响,我的理解是如果参数初始化的数量级和输入神经元的数量级相近,而学习率又比较小的话,很有可能会导致模型学习过慢或者效率很低下的结果。
3:损失函数数值的问题,关于之前的损失函数我有一些理解错误,之前神经网络的损失函数最多只能下降到8左右,那是因为sigmoid(x)函数只能逼近1,然后我用数字5训练的图像,带入误差函数之后就会得到8左右的数值,因此这个数值说明不了什么问题,神经网络的目标是找到使得误差函数最小的参数数值。
神经网络结果
我采用了784个输入神经元,第一个隐层16个神经元,第二个隐层18个神经元,输出层有10个神经元。
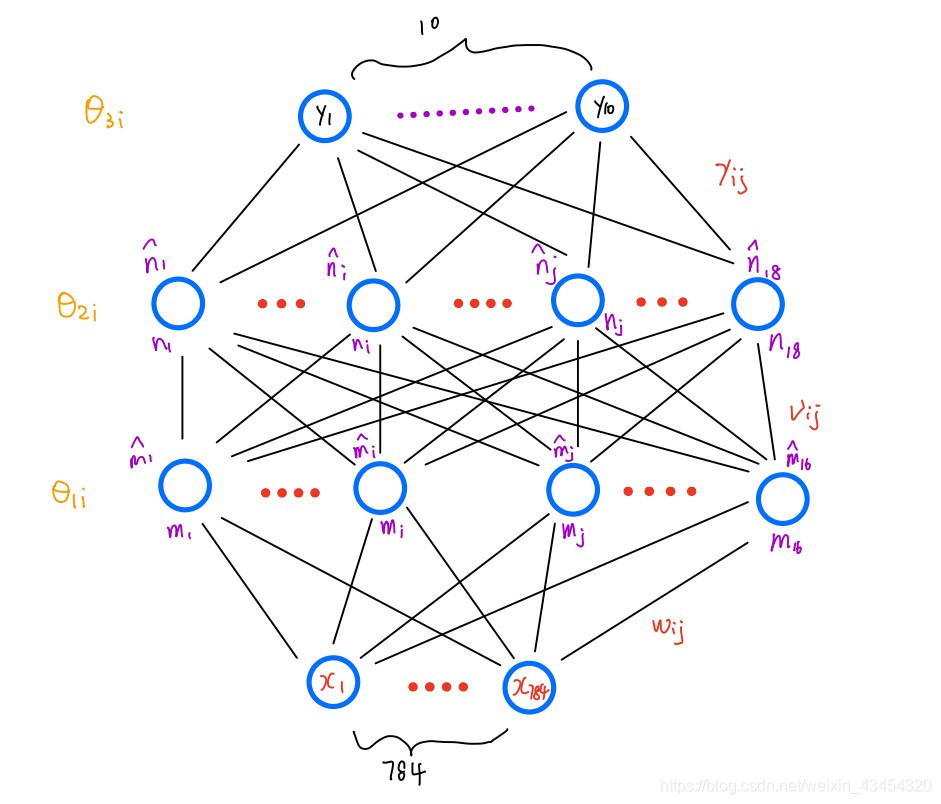
损失函数采用均方根值:

权重梯度下降公式:

阈值下降梯度公式:

正向传递公式:
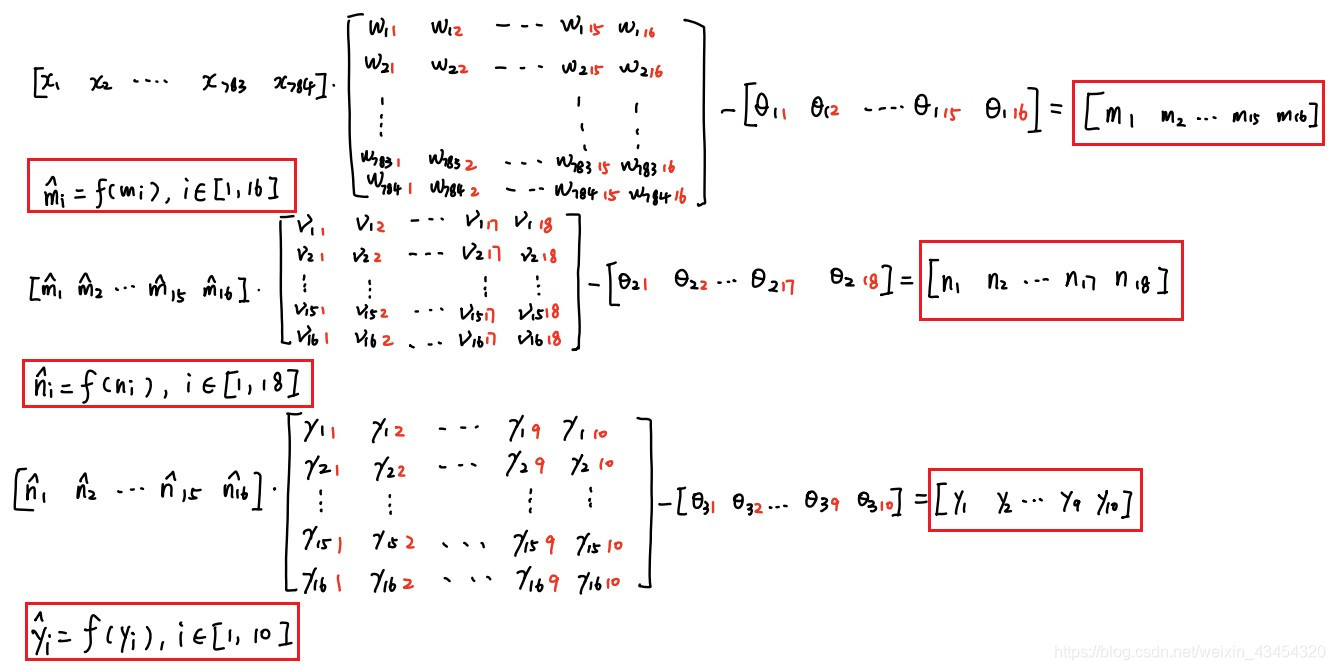
明天任务
明天需要重新实现一个这个神经网络,这个是比较快的,只需要更新一下公式即可,更重要的是需要看一下这个神经网络的损失函数曲线。

