Neural Network Basics
1.Logistic Regression
一个用于二分分类(Binary Classification)的算法。
逻辑回归问题可以看成是一个简单的神经网络,只包含一个神经元。
引例:IsCat
问题可描述为如下神经网络:
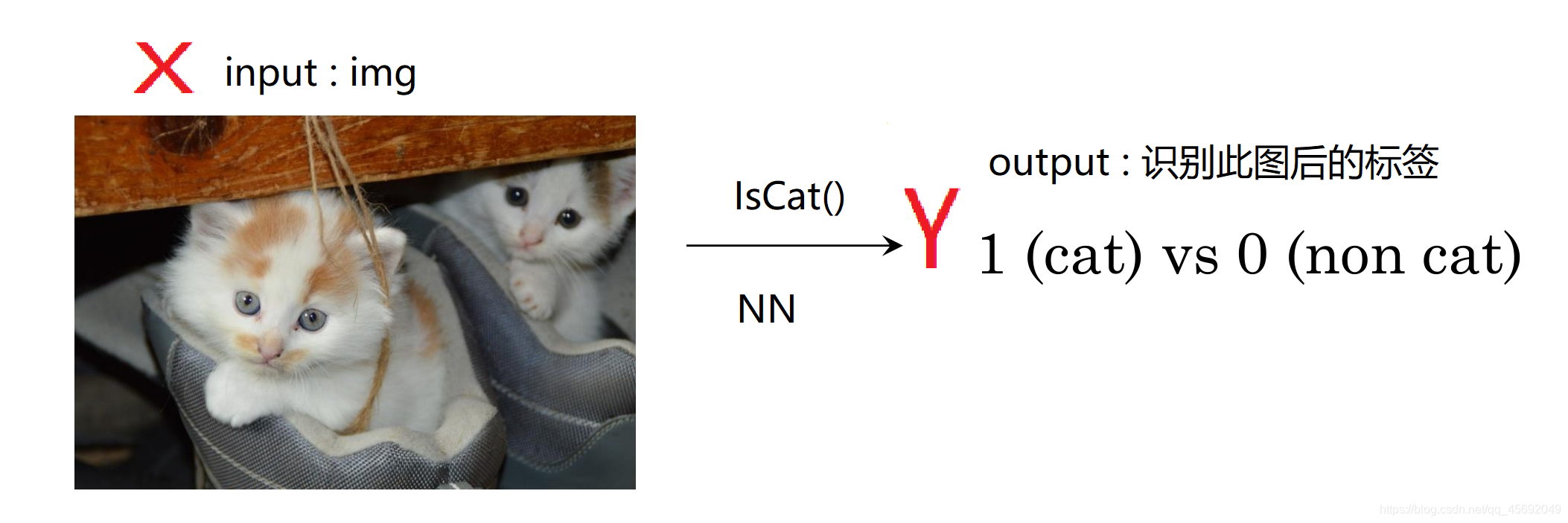
图片在计算机中如何表示?
计算机存储了3个独立矩阵,分别对应下图red、green、blue三个颜色通道。
三个矩阵的大小与图片大小相等,此该问题下都为64 × 64矩阵(图中简化为5 × 4的小矩阵),矩阵各行各列的值都是0-255,表示像素的亮度。
在二分分类问题中,目标是训练出一个分类器。以图片的特征向量x作为输入,输出为预测标签y(0/1)。具体实现如下图:
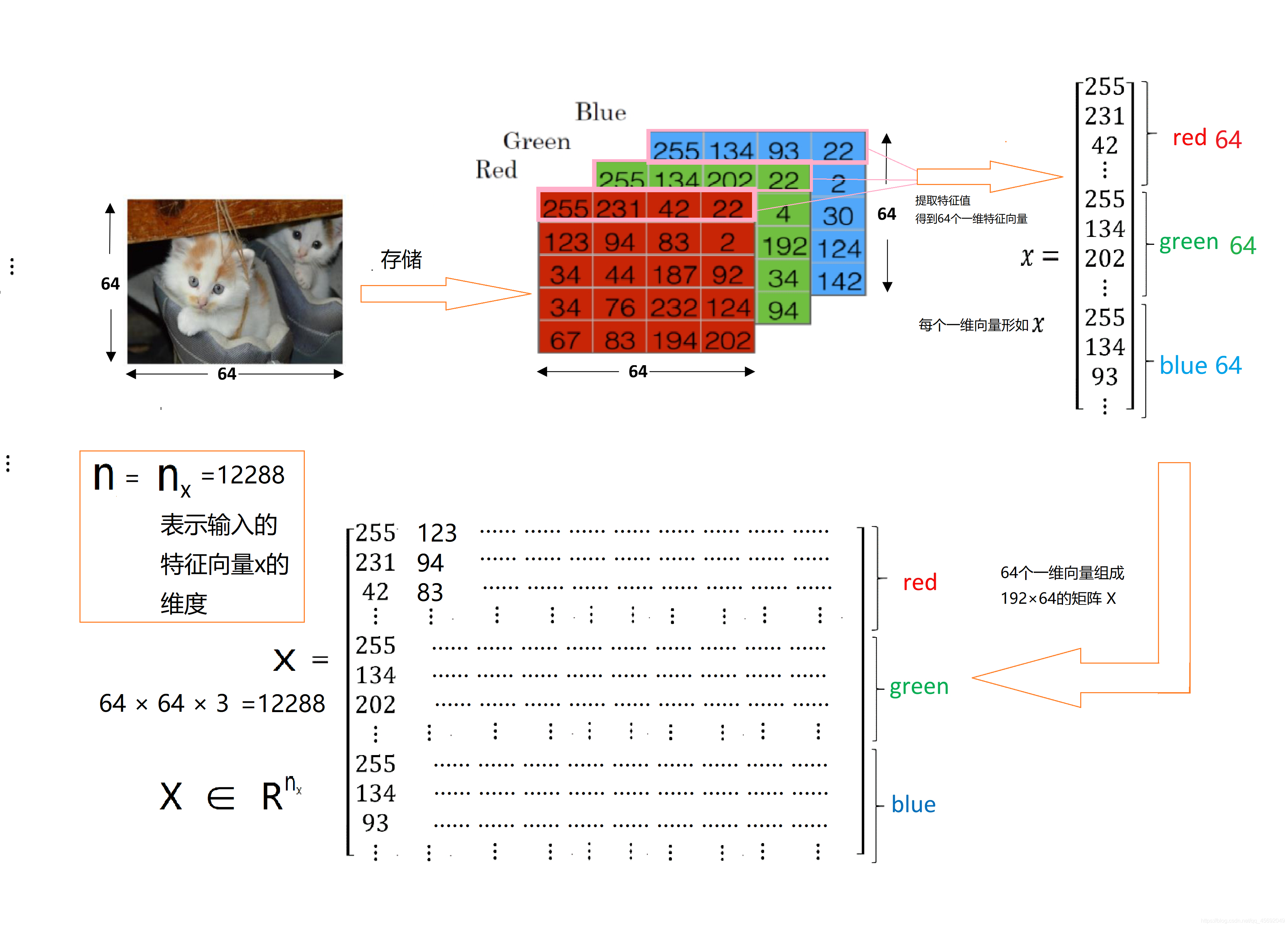
Notation
nx、Rn、mtrain 、mtest

shape函数 用于输出矩阵的维度
逻辑回归模型
基本概念
损失/函数(Loss Function) 是定义在 单个样本上的,算的是单个样本的误差。一般用L表示。用来衡量算法的运行情况,即衡量预测值与实际值有多接近。
为了训练逻辑模型中的参数w和b,需要定义一个成本/代价函数(Cost Function )。它是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均,一般用J表示。这给我们评价学习效果提供了一个标准,提出这个后下一步要做的就是不断优化神经网络,来减小成本/代价函数的值,即在逻辑模型训练过程中,找到合适的参数,使J尽可能小。
具体思路

线性输出区间为整个实数范围,而逻辑回归要求输出范围在[0,1]之间,所以还需要对上式的线性函数输出进行处理。方法是引入Sigmoid函数,让输出限定在[0,1]之间。
Sigmoid函数是一种非线性的S型函数,输出被限定在[0,1]之间,通常被用在神经网络中当作激活函数(Activation function)使用。Sigmoid函数的表达式和曲线如下所示:
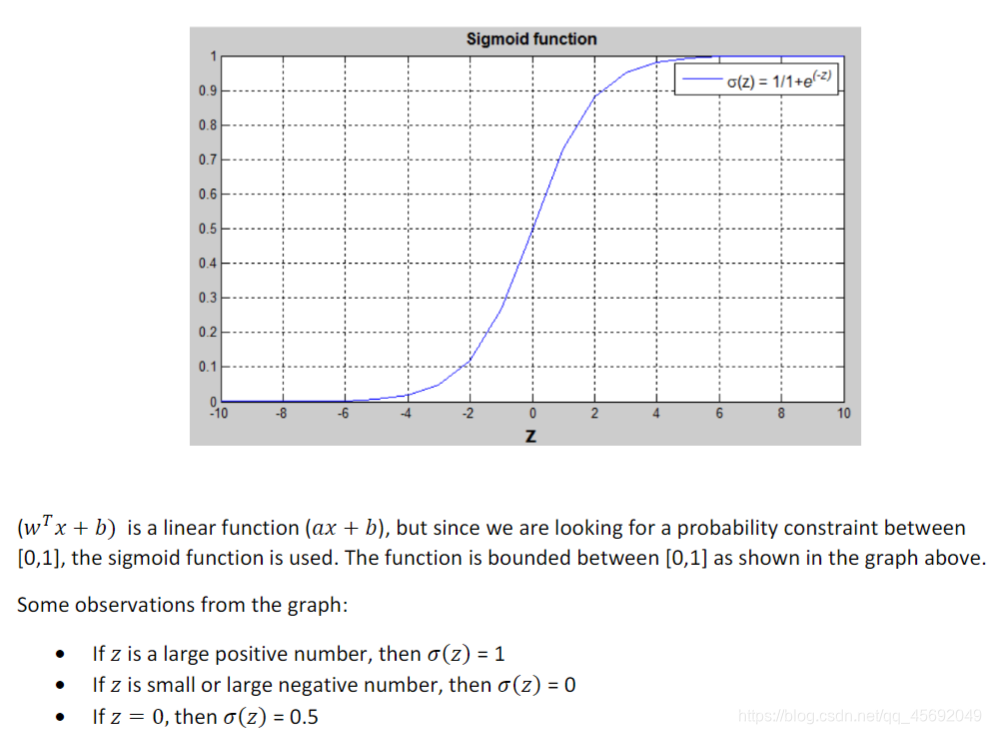
Sigmoid函数的一阶导数可以用其自身表示:
σ′(z)=σ(z)(1?σ(z)) (后面求导会用到)
这样,通过Sigmoid函数,就能够将逻辑回归的输出限定在[0,1]之间了。
损失/误差函数(loss/error fuction)和成本/代价函数(Cost Function )的定义:
1)虽然用差平方或其1/2这样定义损失函数,理论上是可行的。但在逻辑回归中,我们通常不这样定义,因为原因是这种Loss function一般是non-convex的。non-convex函数在使用梯度下降算法时,容易得到局部最小值(local minumum),即局部最优化。而我们最优化的目标是计算得到全局最优化(Global optimization)。因此,我们一般选择的Loss function应该是convex的。
2)成本/代价函数是损失函数的平均。
基于以上两点,做出如下分析:

损失函数
2.Gradient Descent
w可以是实数,也可以是更高维的向量,为方便理解,以w是实数为例作图如下。我们的目的是用梯度下降法来计算出合适的w和b值,从而最小化m个训练样本的Cost function,即J(w,b)。
由于J(w,b)是convex function,梯度下降算法是先随机选择一组参数w和b值(对于逻辑回归,任意初始化都是有效的,通常用0初始化),然后每次迭代的过程中分别沿着w和b的梯度(偏导数)的反方向前进一小步(沿最陡的下坡方向走),不断修正w和b。每次迭代更新w和b后,都能让J(w,b)更接近全局最小值。梯度下降的过程如下图所示。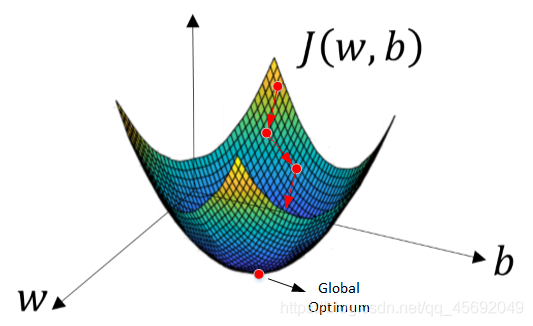
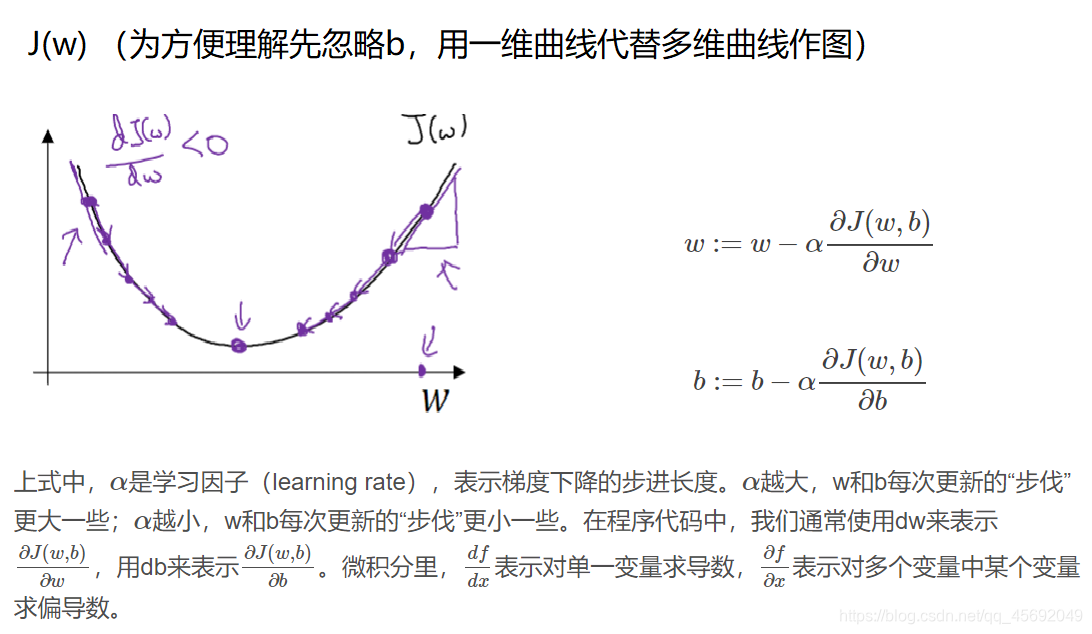
: = 是覆盖之前的值
?= 是如果没有被赋值过就赋予等号后面的值
3.Forward and Back Propagation
整个神经网络的训练过程实际上包含了两个过程:正向传播(Forward Propagation)和反向传播(Back Propagation)。正向传播是从输入到输出,由神经网络计算得到预测输出的过程;反向传播是从输出到输入,对参数w和b计算梯度的过程。
计算图的正向传播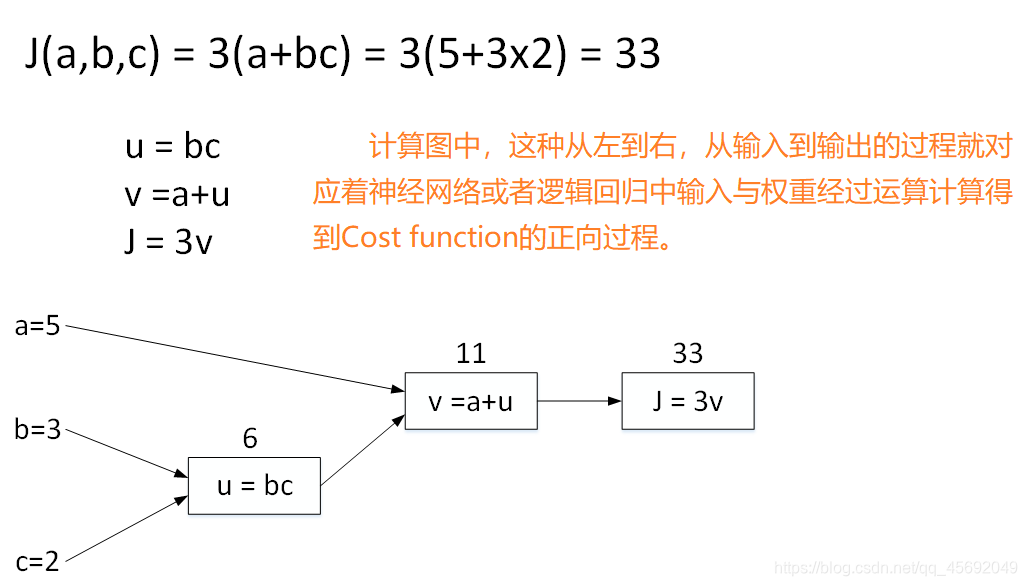
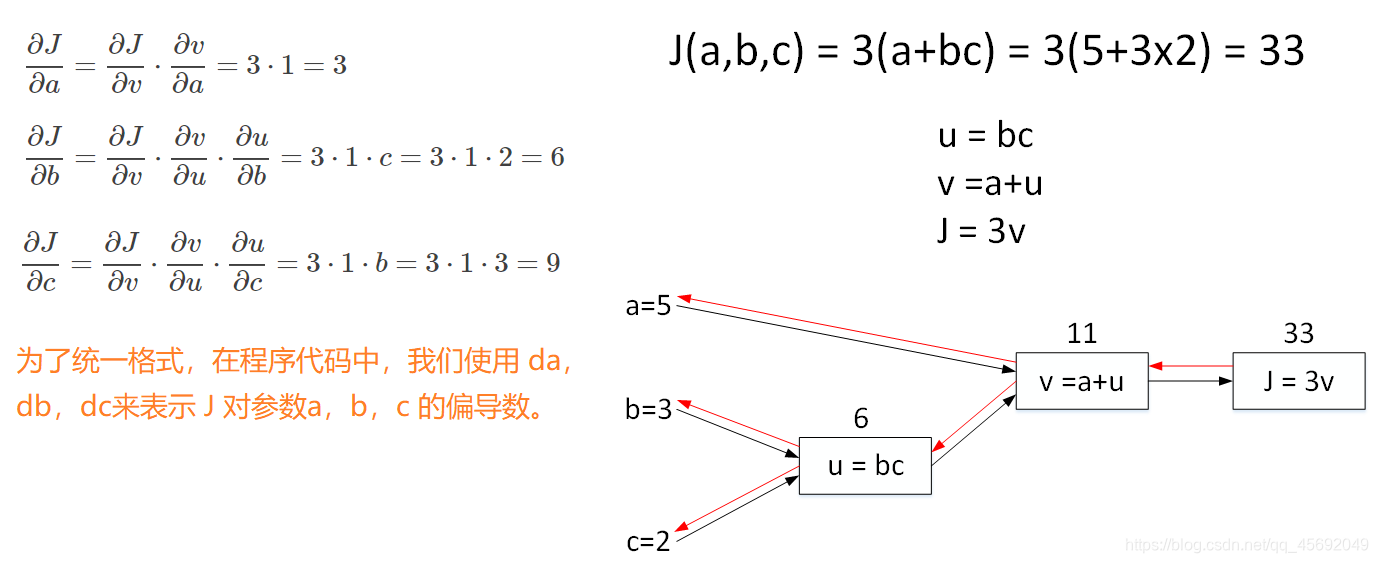
计算图的反向传播
微积分、链式法则
4. Gradient Descent for Logistic Regression
在单个样本上的梯度下降
该逻辑回归的正向传播过程如下:
w 和 x看作列向量

计算该逻辑回归的反向传播过程,即由Loss function计算参数w和b的偏导数:

在整体训练集上的梯度下降
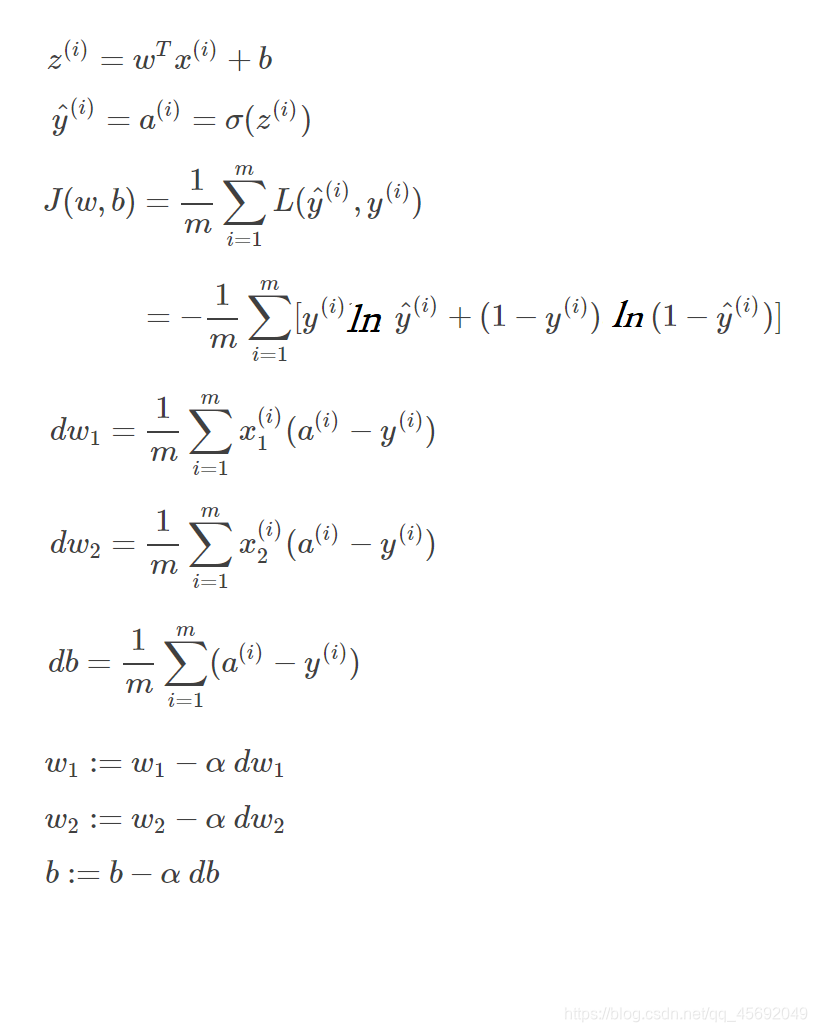
2次for循环:样本从1-m的循环,计算dw时用循环
#伪代码
J=0; dw1=0; dw2=0; db=0
# dw1、dw2、db都作为累加器
for i in range(1,m+1):
z(i) = wx(i)+b
a(i) = sigmoid(z(i))
J += -[y(i)ln(a(i))+(1-y(i))ln(1-a(i))
dz(i) = a(i)-y(i)
dw1 += x1(i)dz(i)
dw2 += x2(i)dz(i)
db += dz(i)
J /= m
dw1 /= m
dw2 /= m
db /= m
5.vectorization
在深度学习中,样本数量m通常很大,使用for循环会让神经网络程序运行得很慢。所以,我们应该尽量避免使用for循环操作,而使用矩阵运算,能够大大提高程序运行速度。
向量化:消除代码中显式的for循环
掌握numpy:如dot()、exp()、sum()、zeros()
向量化与非向量化 代码运行时间的比较(以函数dot()为例)
import numpy as np
import time
w = np.random.rand(1000000)
x = np.random.rand(1000000)
#向量化
start1 = time.time()
z = np.dot(w,x)
end1 = time.time()
print(z)
print("vectorization_time:"+str(1000*(end1-start1))+"ms")
#非向量化
z = 0
start2 = time.time()
for i in range(1000000):
z += w[i]*x[i]
end2 = time.time()
print(z)
print("loop_time:"+str(1000*(end2-start2))+"ms")
函数sigmoid()的定义:
def sigmoid(z):
# 参数:z —— 任何大小的标量或numpy数组。
# 返回:s —— sigmoid(z)
s = 1 / (1 + np.exp(-z))
return s
正向传播
一步向量化实现,同时处理m个训练样本:
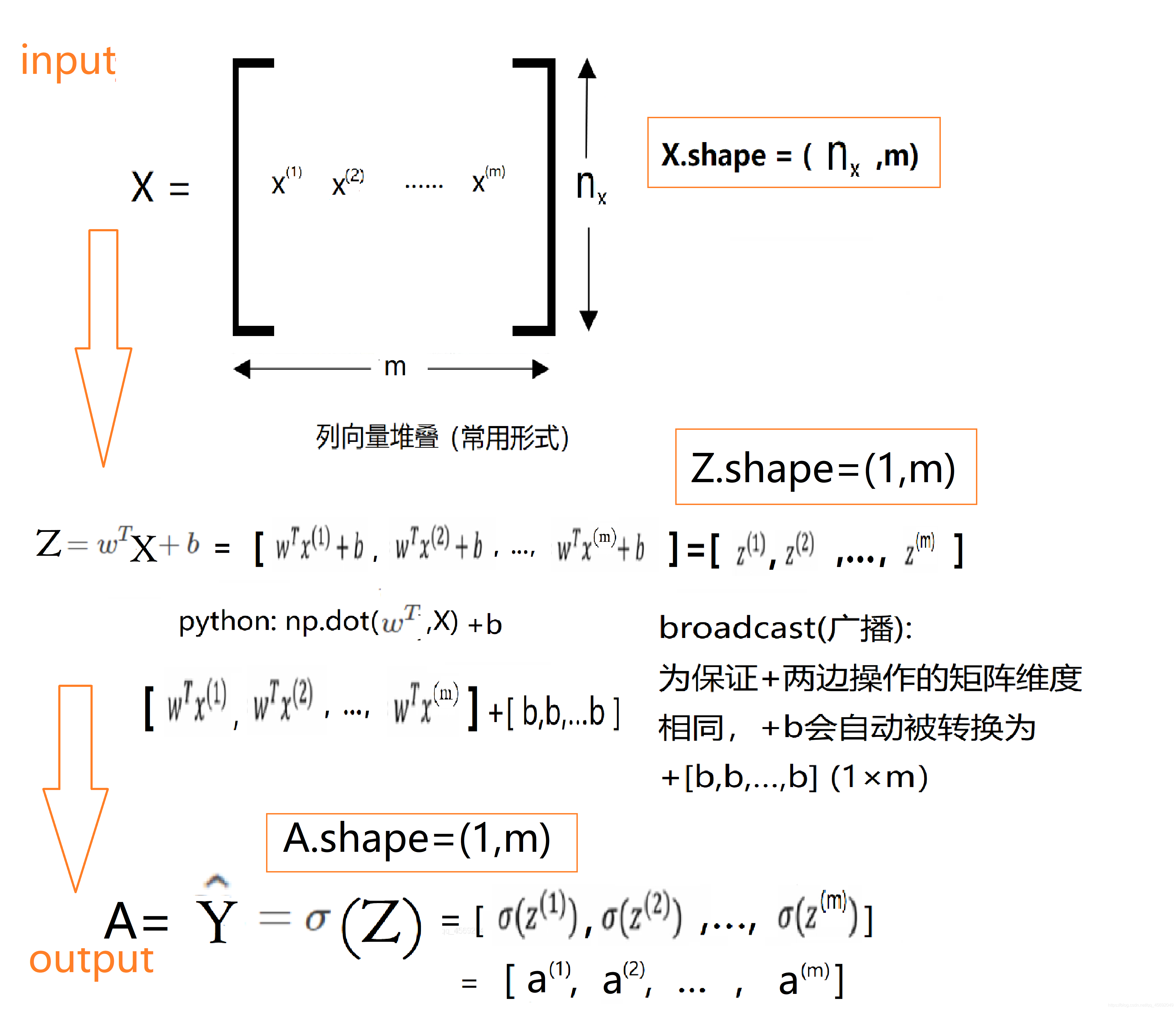
广播(broadcasting)
可以通过下图形象地理解:
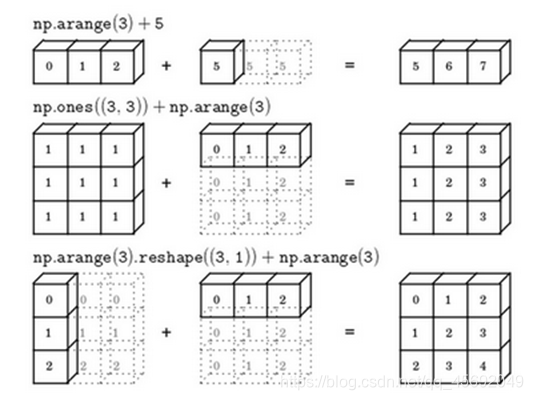
反向传播
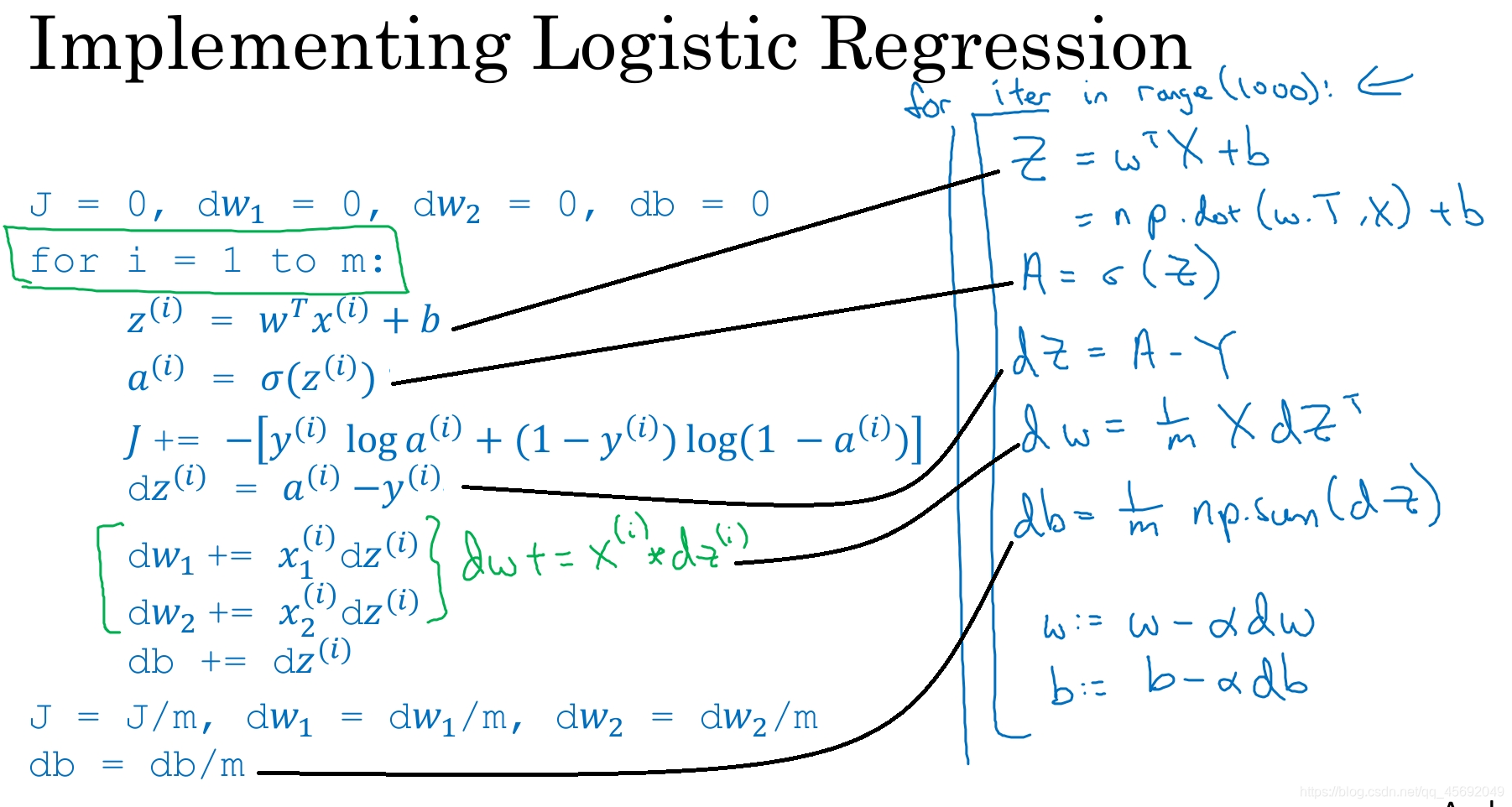
如果希望多次迭代进行梯度下降,那么仍然需要for循环,放在最外层。
tips:
1)减少秩为1的矩阵的使用
2)如果不完全确定一个向量的维度(dimension),使用断言语句(assertion statement)。如图确保在这种情况下是一个维度为(5,1)的向量/列向量。这些断言语句实际上是要去执行的,并且它们也会有助于为你的代码提供信息。
3)重新改变数组维数 a=reshape,表明一个(5,1)数组或者一个(1,5)数组,以致于它表现更像列向量或行向量。

