[人工智能]NLP中的Transformer的学习【正在编辑】

NLP中的Transformer操作总结

本文只作为笔者的学习笔记，记录了笔者从零开始接触NLP的过程。
文章引用了各个渠道的资料，但全部是个人总结的结果。渠道包括但不限于：CSDN，GitHub，知乎，Wikipedia，各类书籍，期刊与会议，课程教材等。本文可能包含您或您见过的各种资料，笔者已尽可能加入了引用的地址。如有纠正与补充，欢迎指正。

前言

以下是废话
开始学习：现在是2021/08/06，作为一个刚刚拿到EIE学士学位的萌新…决定继续申请PhD学位的我看中了NLP这个貌似还算可以的方向。由于本科只有做Speech Enhancement的经历，NLP从哪里入手也是个大问题。和一个认识的UCL的教授讨论了一下，决定还是先找个突破口入门。随便Google了一下，打算从attention和semantic representation入手。当然，只了解方法或者模型而不去弄明白他是干什么的显然毫无意义。于是有了如下笔记。本文将以Transformer为主题，记录我作为初学者的学习经过。

现在进入正文

一、Encoder-Decoder：编码译码器

机器翻译有助于提高翻译速度。最简单的机器翻译可以通过编码译码器实现。Encoder-Decoder 通常称作——编码器-解码器，是深度学习中常见的模型框架，很多常见的应用都是利用编码-解码框架设计的。

1. Encoder-decoder 定义：

是一个通用的框架，而非具体的模型

Encoder 和 Decoder 部分可以是任意文字，语音，图像，视频数据，模型可以是 CNN，RNN，LSTM，GRU，Attention 等等。所以，基于 Encoder-Decoder，我们可以设计出各种各样的模型。

编码：将输入序列转化成一个固定长度向量
解码：将之前生成的固定向量再转化出输出序列
encoder-decoder的特征：Sequence-to-sequence也称为end to end

2. Seq2Seq：

Seq2Seq ( Sequence-to-sequence 的缩写)，就如字面意思，输入一个序列，输出另一个序列。
这种结构最重要的地方在于输入序列和输出序列的长度是可变的。

在机器翻译里面，如下图，将英语 「it is a cat.」翻译成汉语 「这是一只猫」，输入 4 个单词，输出5个汉字。

在训练数据集中，我们可以在每个句子后附特殊字符 (end of sequence) 以表示序列终止，每个句子前用到了特殊字符 (begin of sequence) 表示序列开始。

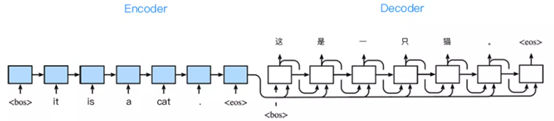
将英文“It is a cat.”翻译成中文的流程

1. 符号化处理，句首句尾用符号标记，此时句子变为：“<bos> it is a cat . <eos>”
2. 对序列进行建模，得到概率最大的译文序列片段：第一个词“it”译为“这”，将生成的词加入以为序列，对序列中每一个片段采取同样步骤，直到序列末尾的eos
3. 识别到eos后，停止迭代，进行反符号处理，得到译文

3. Attention 机制的引入：应对Encoder-Decoder 的缺陷

Encoder-Decoder 的缺陷实际上是RNN（Recurrent Neural Network）的缺陷——长程梯度消失。

Attention 就是为了解决信息过长导致信息丢失的问题，Attention 名为注意力机制

就像我们平时读文章一样，我们的视线不可能注意到所有的文字，随着眼睛的移动，我们的注意力也会跟着视线转移，最终会停留在认为重要的单词上，甚至还会划重点。一般来说，一篇文章的标题，小标题，我们都会第一时间注意到，这就是注意力机制。
神经网络中的注意力模型借鉴了我们人脑的这一功能，让神经网络模型对输入数据的不同部位的关注点不一样，权重不一样。

与attention相关的论文：Show, Attend and Tell
Show, Attend and Tell的TensorFlow实现：Click Here

1. 在 Attention 模型中，我们翻译当前词，会寻找与源语句中相对应的几个词语，然后结合之前已经翻译的序列来翻译下一个词。
2. 注意力模型的建模和实现：
   

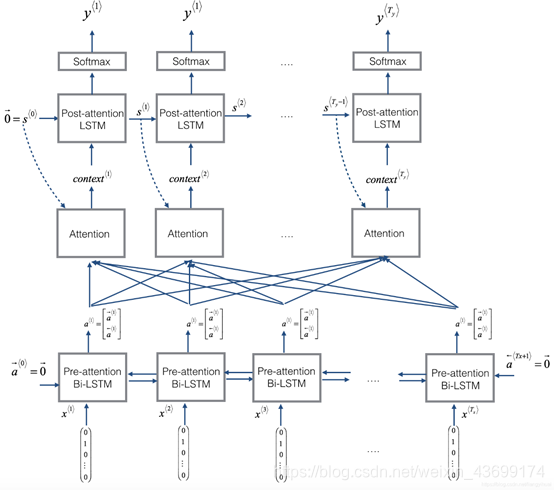
本章参考1：Encoder-decoder
本章参考2：Attention Model

二、

总结

一些零散的基础知识

用作补充，可以先跳过
移步：二、Encoder-Decoder

1.Softmax函数：

Softmax函数用于：把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。
假设有一个数组$V$,$V_i$ 表示$V$中的第$i$个元素，那么这个元素的softmax值为:
$$S_i=\frac{e^i}{{\sum }_j{e}^j}$$
该元素的softmax值，就是该元素的指数与所有元素指数和的比值。

这个定义可以说很简单，也很直观。那为什么要定义成这个形式呢？原因主要如下。

1. softmax设计的初衷，是希望特征对概率的影响是乘性的。
2. 多类分类问题的目标函数常常选为cross-entropy。即$$L=?\sum _k{t}_k?\ln P(y=k)$$，其中目标类的$t_k$为1，其余类的$t_k$为0。
   在神经网络模型中(最简单的logistic regression也可看成没有隐含层的神经网络)，输出层第$i$个神经元的输入为$${\alpha }_i=\sum _d{w}_{id}{x}_d$$
   神经网络是用后向传播算法error back-propagation训练的，这个过程中的关键量是$?L/?{\alpha }_i$
3. softmax很简单的求导：
   在多分类问题中，我们经常使用交叉熵作为损失函数
   $$\text{?Loss?}=?\sum _i{t}_i\ln y_i$$
   其中，$t_i$表示真实值，$y_i$表示softmax值。假设$t_i=1$，则预测第$i$个Loss时有
   $$\mathrm{Los}{s}_i=?\ln y_i$$
   通过复杂变换（见参考）后可得导数为：
   $$\frac{?{\text{?Loss?}}_i}{{?}_i}=?\frac{?\ln y_i}{{?}_i}=y_i?1$$
   因此，正向传播算法求出$y_i$后，减1即可得逆向传播算法的梯度！

本节参考

2. RNN：

1. 单个RNN的基本形式
   
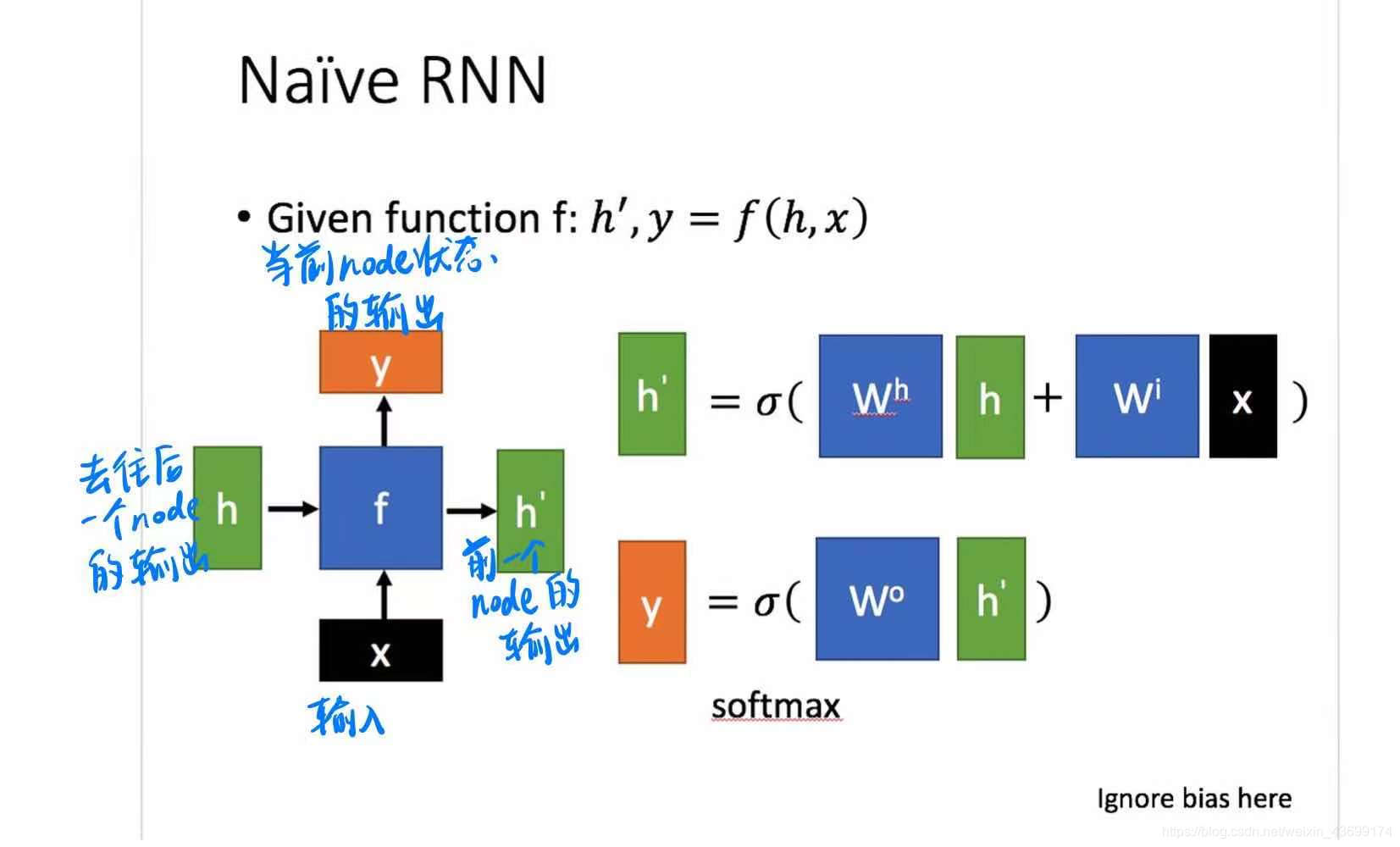
   通过上图的公式可以看到，输出 h’ 与 x 和 h 的值都相关。
2. 而对于序列形式的输入，我们能够得到如下形式的RNN：
   
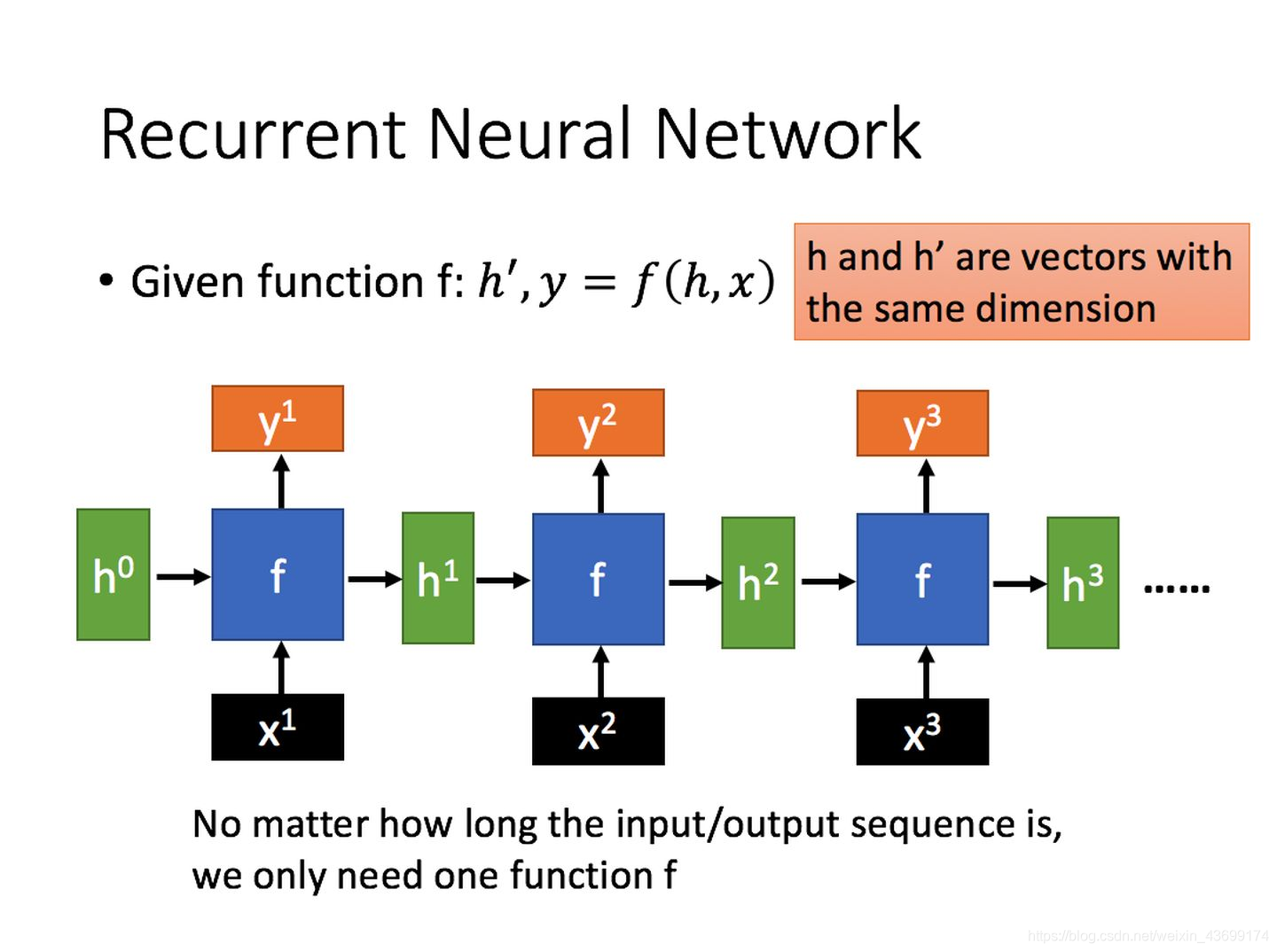
   本节参考

3. LSTM：

长短期记忆（Long short-term memory, LSTM）是一种特殊的RNN，主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说，就是相比普通的RNN，LSTM能够在更长的序列中有更好的表现。

1. LSTM与basic RNN的区别：左basic RNN，右LSTM
   
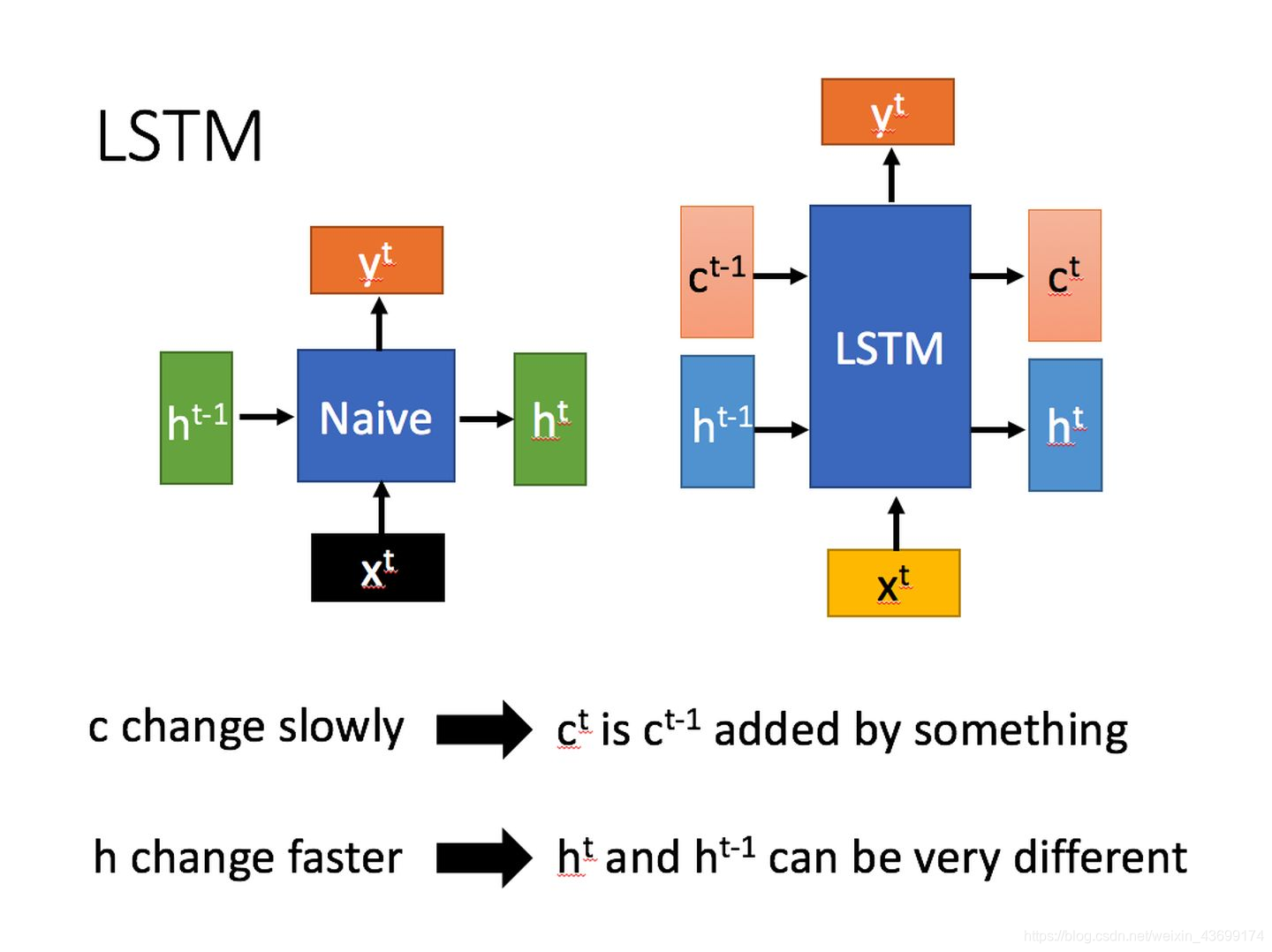
   相比RNN只有一个传递状态$h^t$，LSTM有两个传输状态：$C^t$（cell state）和$h^t$（hidden state）。然而basic RNN中的$h^t$相当于LSTM的$C^t$。其中$C^t$改变很慢，而不同node下$h^t$变化很大。
2. LSTM的四种状态
   如图所示，使用LSTM的当前输入$x^t$和上一状态传递进入的$h^{t?1}$进行矩阵拼接并且乘以对应的权重矩阵$W$后可得四种状态
   
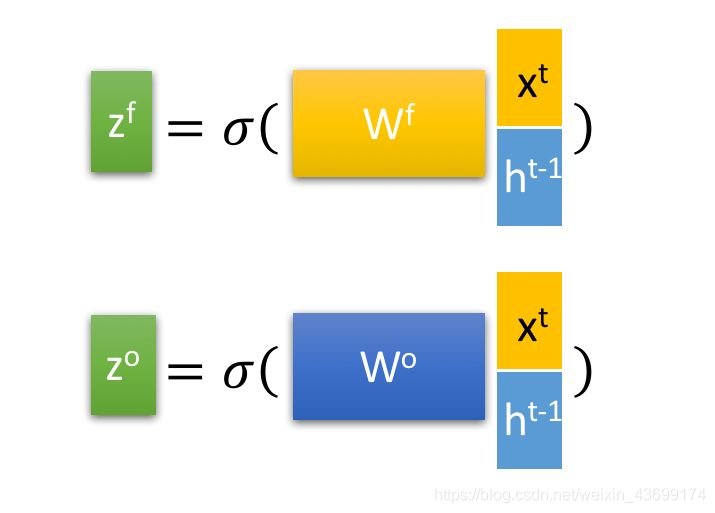
   其中，$z^i$，$z^f$，$z^o$在乘以权重矩阵后，将再通过一个sigmoid函数转换到区间$[0,1]$，来作为一种门控状态。而 $z$ 则是将结果通过一个 $tanh$ 激活函数转换到区间$[0,1]$（这里使用 $tanh$ 是因为这里是将其做为输入数据，而不是门控信号）。
3. 四种状态在LSTM中的使用：
   
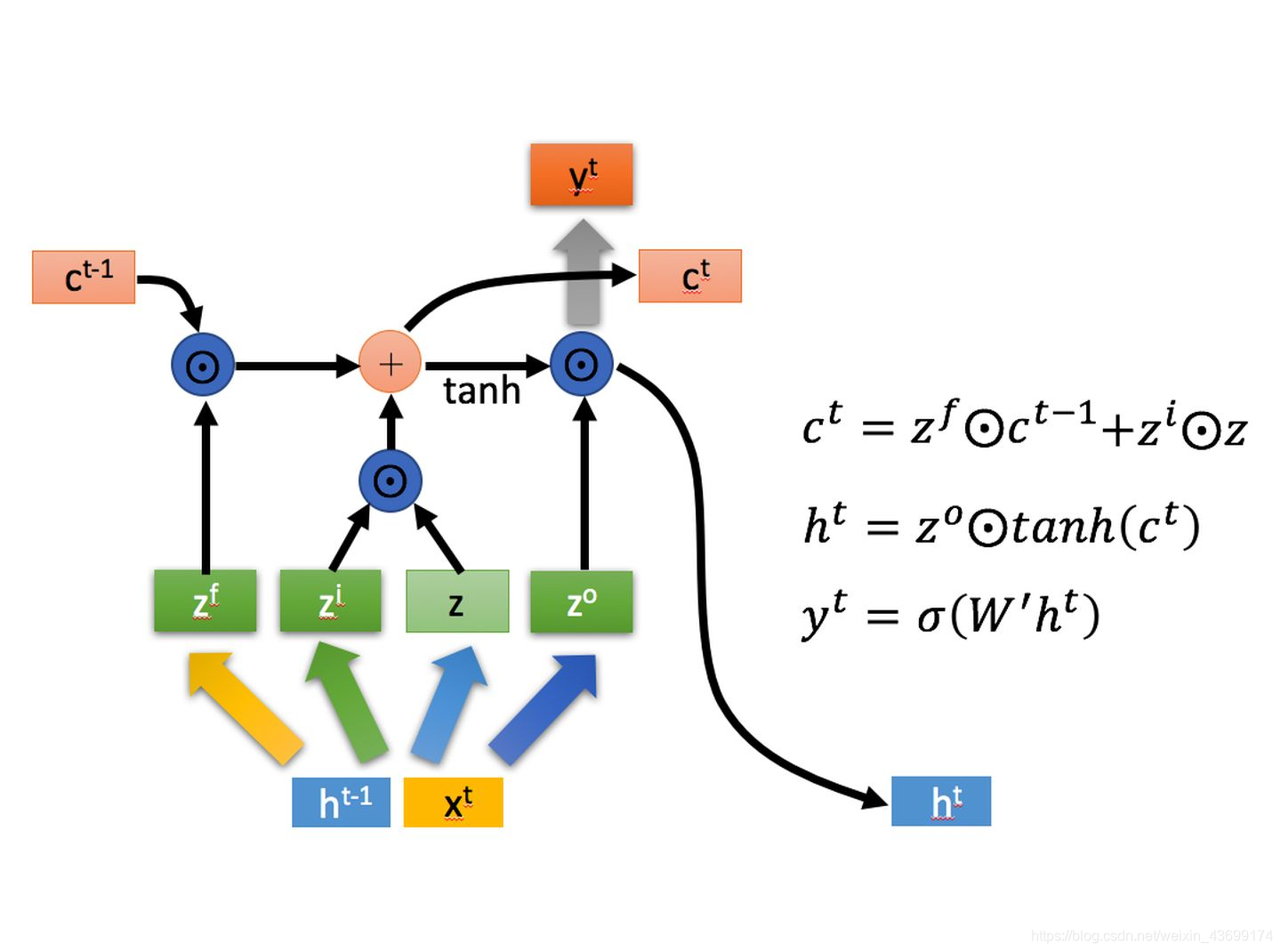
   其中 $?$ 与 $?$ 分别代表矩阵对应相乘（Hadamard Product）和相加，因此要求两个矩阵是同型的。
   a. 忘记阶段：选择性忘记——忘记不重要的，记住重要的
   具体来说是通过计算得到的 $z^f$ （$f$表示forget）来作为忘记门控，来控制上一个状态的 $c^{t?1}$ 哪些需要留哪些需要忘。
   b. 选择记忆阶段：对输入 $x^t$ 进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的 $z$ 表示。而选择的门控信号则是由 $z^i$ （$i$代表information）来进行控制。
   将上面两步得到的结果相加，即可得到传输给下一个状态的 $c^t$ 。也就是上图中的第一个公式。
   c. 输出阶段：这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 $z^o$ 来进行控制的。并且还对上一阶段得到的 $c^o$ 进行了放缩（通过一个tanh激活函数进行变化）。如上图第二个公式。
   与普通RNN类似，输出 $y^t$ 往往最终也是通过 $h^t$ 变化得到。如上图第三个公式。

LSTM因为引入了很多内容，导致参数变多，也使得训练难度加大了很多。因此很多时候我们往往会使用效果和LSTM相当但参数更少的GRU来构建大训练量的模型。

本节参考