[人工智能]数据分析2——探索性数据分析（多因子与复合分析）

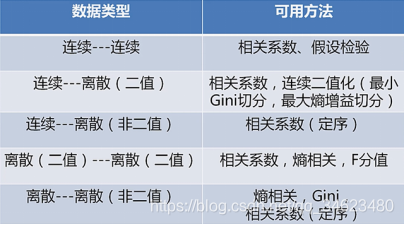
理论铺垫：假设检验与方差检验；相关系数：皮尔逊、斯皮尔曼；回归：线性回归；PCA与奇异值分解

1、假设检验

（1）建立原假设Ho(包含等号)，H0的反命题为H1，也叫备择假设。
（2）选择检验统计量
（3）根据显著水平(一般为0.05)，确定拒绝域
（4）计算p值或样本统计值，作出判断。（若p<显著水平，则假设为假，反之）
说明：显著水平：我们一般可以接受的假设的最大失真程度。它和相似度加和为1。显著水平一般是人为定的，值越低，表示对数据和分布程度的契合度要求越高。检验方法：P检验常用来比较两组样本分布是否一致、f检验（方差检验）常用于方差分析、卡方检验常用于检验两个因素之间是否有着比较强的联系。
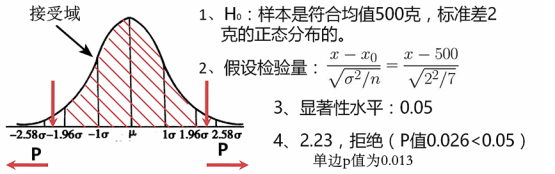
例1：洗衣粉标准重量500g，标准差2g。
数据：501.8、502.4、499、500.3、504.5、498.2、505.6

例2：检验化妆这个行为于性别是否有关，得到数据如下。

注：f表示实际化妆人数的值，np表示假设化妆人数的值。
假设化妆这个行为于性别无关，从而得到假设值在上图括号中。

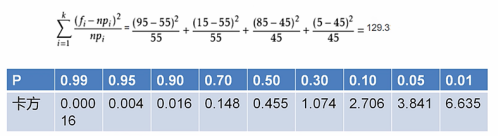
经过计算可以得到，当p=0.05时，129.3>3.841，所以假设不成立。
例：数据可以分为m组，共n个采样。这里m=3,n=15

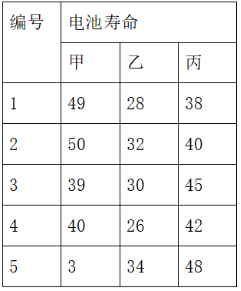
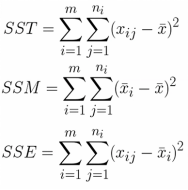
说明：ni指的是每组数据的数量即5；n指的是所有的数据即15
SST总变差平方和；SSM平均（组间）平方和；SSE组内平方和。

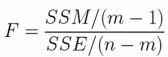
检测统计量F，做假设检验（F满足自由度( m-1, n-m )的F分布）
假设甲乙丙三者均值一定，没有差别，统计量为F，p=0.05
均值：x=38.93 x1=44.2 x2=30 x3=42.6
SSM = 604.93 SSE = 206 F = 17.62 查表得到P = 0.00027 < 0.05 拒绝原假设
例：独立t分布检验（样本一，样本二）

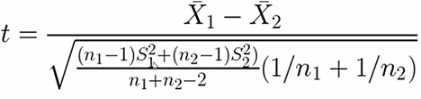
import numpy as np
import scipy.stats as ss

#生成符合标准正态分布的20个数
norm_dist = ss.norm.rvs(size = 20)
print(norm_dist)

#检测是否是正态分布
#normaltest是基于偏度和峰度得到检验方法
ss.normaltest(norm_dist)  
#结果：NormaltestResult(statistic=0.6275445660268315, pvalue=0.7306853986931392)

#利用之前例子中的卡方检验来看normaltest是否属于正态分布
#表格中实际值化妆的男女是15,95；不化妆的是85,5
ss.chi2_contingency([[15,95],[85,5]])
#得到的结果：检验统计量；P值；自由度；理论分布

#利用独立t分布检验(需要两个样本)
ss.ttest_ind(ss.norm.rvs(size = 10),ss.norm.rvs(size = 20))
#得到的结果：检验统计量；P值；

#利用方差检验（f检验）
ss.f_oneway([49,50,39,40,43],[28,32,30,26,34],[38,40,45,42,48])
#得到的结果：检验统计量；P值；

#做一个qq图
from statsmodels.graphics.api import qqplot
from matplotlib import pyplot as plt

#qq图默认检验一个图是否是正态分布
plt.show(qqplot(ss.norm.rvs(size = 20)))
#得到一个分布可以先找到它的分位数，然后对应的分布找到正态分布的分位数
#qq图X轴为正态分布的分位数的值，Y轴我们已知分布的值，这样就可以得到一个散点图
#若散点图和X,Y轴的角平分线重合，则可认为已知分布的值符合正态分布

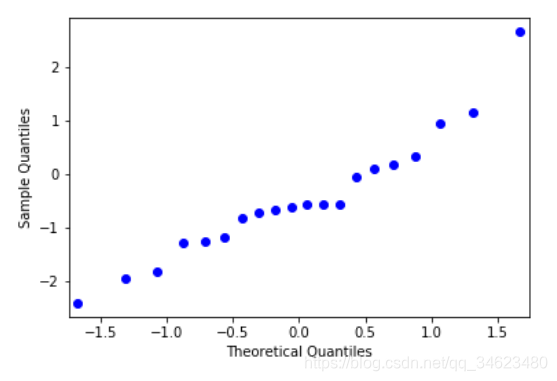
2、相关系数

X,Y相关系数趋近于1则正相关；趋近于-1则负相关；0则无关。
Pearson相关系数

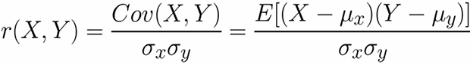
Spearman相关系数

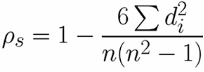
区别：Spearman相关系数只和名次差di有关，与数值无关

#相关系数
import pandas as pd
s1=pd.Series([0.1,0.2,1.1,2.4,1.3,0.3,0.5])
s2=pd.Series([0.5,0.4,1.2,2.5,1.1,0.7,0.1])

#利用corr()函数直接对s1,s2进行相关系数的对比
s1.corr(s2)  
#结果：0.9333729600465923

#利用spearman相关系数
s1.corr(s2,method="spearman")
#结果：0.7142857142857144

#直接利用DataFrame对s1,s2进行相关系数的计算，DataFrame是针对列进行计算的
df=pd.DataFrame([s1,s2])
df.corr()
#结果如图一

#求个转置再进行计算
df=pd.DataFrame(np.array([s1,s2]).T)
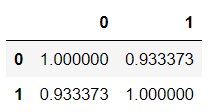
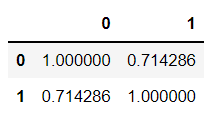
df.corr()	#结果如图二
df.corr(method="spearman")	#结果如图三

图一：

图二：

图三：

3、线性回归

回归：确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。若关系为线性则是线性回归。

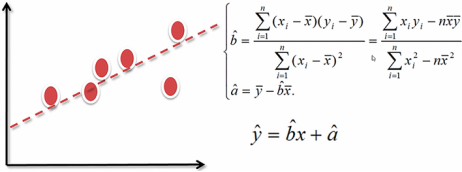
线性回归的效果主要与以下两个指标相关：
决定系数（R）（一元和多元式子如下）和残差不相关（DW检验）

说明：R越接近于1，则回归效果越好；越接近于0，则越差。K指的是参数的个数；e指的是残差即预测值与实际值的差；DW范围是0~4，接近于4表示残差正相关；接近于0则是负相关；为2则是无关。好的回归残差是不相关的。

#回归的例子
#astype()强制类型转换为float。
#重新指定一下形状，把每一个元素都当成数组来看，所以reshape一下
x=np.arange(10).astype(np.float).reshape((10,1))
#y=x*3+4,3和4就是要求的系数，我们在这加点噪声,但形状保持一致(10,1)
y=x*3+4+np.random.random((10,1))

from sklearn.linear_model import LinearRegression

#构建一个线性回归
reg=LinearRegression()
#拟合
res=reg.fit(x,y)
#求预测值
y_ped=reg.predict(x)
print("预测值:",y_ped)
#求系数，截距
print("系数:",reg.coef_)	#系数: [[2.94447142]]
print("截距:",reg.intercept_)	#截距: [4.70831619]

4、主成分分析（PCA）

主成分分析是一种统计方法，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。
主成分分析步骤：求特征协方差矩阵；求协方差的特征值和特征向量；将特征值按照从大到小的顺序排序，选择其中最大的k个；将样本点投影到选取的特征向量上
奇异值分解（SVD）：特征矩阵A分解为mm的酉阵U，mn半正定矩阵(奇异值阵) ，n*n酉阵转置V。
说明：酉阵在实数域是单位矩阵的意思，U代表在当前空间下的一组正交基,V代表在变换后的空间下的正交基。通过调整奇异值矩阵的奇异值维度，就可以在尽可能保留主要信息的维度下，减少数据的维度。

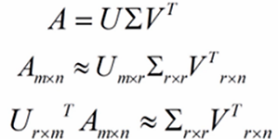
#sklearn'decomposition利用的是奇异值分解的方法
from sklearn.decomposition import PCA

#降维(这里是降为一维)
lower_dim=PCA(n_components=1)
lower_dim.fit(data)
#结果：PCA(copy=True, iterated_power='auto', n_components=1, random_state=None,
# svd_solver='auto', tol=0.0, whiten=False)

#降维后的信息量为96%
lower_dim.explained_variance_ratio_
#结果：array([0.96318131])

#利用fit_transform()直接得到转换后的数值
lower_dim.fit_transform(data)

#自定义一个PCA方法
def myPCA(data,n_components=100000):
    #每个属性的均值（针对列）
    mean_vals=np.mean(data,axis=0)
    mid=data-mean_vals
    #协方差计算，rowvar=False表示针对列进行计算
    cov_mat=np.cov(mid,rowvar=False)
    #线性计算
    from scipy import linalg
    #求协方差矩阵特征值、特征向量
    eig_vals,eig_vects=linalg.eig(np.mat(cov_mat))
    
    #取最大特征值所对应的特征向量
    #argsort得到的是排序后的索引即下标
    eig_val_index=np.argsort(eig_vals)
    eig_val_index=eig_val_index[:-(n_components+1):-1]
    eig_vects=eig_vects[:,eig_val_index]
    
    #转换(这里用乘法)
    low_dim_mat=np.dot(mid,eig_vects)
    
    return low_dim_mat,eig_vals

data=np.array([np.array([2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1]),
               np.array([2.4,0.7,2.9,2.2,3,2.7,1.6,1.1,1.6,0.9])]).T
print(myPCA(data,n_components=1))

5、复合分析

交叉分析；因子分析；分组与钻取；相关分析；聚类分析；回归分析

（1）交叉分析：分析属性和属性之间关系的方法。

#交叉分析法一  ——独立t检验分布方法
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

df = pd.read_csv("D:/HR.csv")

#研究各个部门的离职率之间是否有差异
#得到各个部门的离职分布，然后两两之间求他们的t检验统计量，并求出p值
#得到各个部门的离职分布
#得到分组后的索引
dp_indices=df.groupby(by="Department").indices
#print(dp_indices)

sales_values=df["left"].iloc[dp_indices["sales"]].values
technical_values=df["left"].iloc[dp_indices["technical"]].values
#打印t统计量
print(ss.ttest_ind(sales_values,technical_values))
#只打印P值
print(ss.ttest_ind(sales_values,technical_values)[1])
#结果：Ttest_indResult(statistic=-1.0601649378624074, pvalue=0.2891069046174478)

#python 3中所有的key必须加上list
dp_keys=list(dp_indices.keys())

#初始化矩阵,[宽、高]
dp_t_mat=np.zeros([len(dp_keys),len(dp_keys)])
#遍历
for i in range(len(dp_keys)):
    for j in range(len(dp_keys)):
        #求它的独立t检验值
        p_value=ss.ttest_ind(df["left"].iloc[dp_indices[dp_keys[i]]].values,df["left"].iloc[dp_indices[dp_keys[j]]].values)[1]
        if p_value < 0.05:
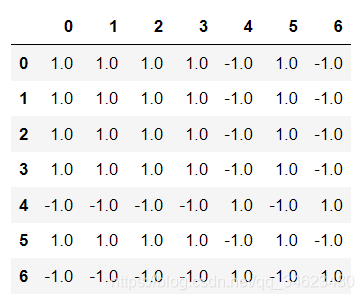
            dp_t_mat[i][j]=-1
        else:
            dp_t_mat[i][j]=p_value
        
#画图
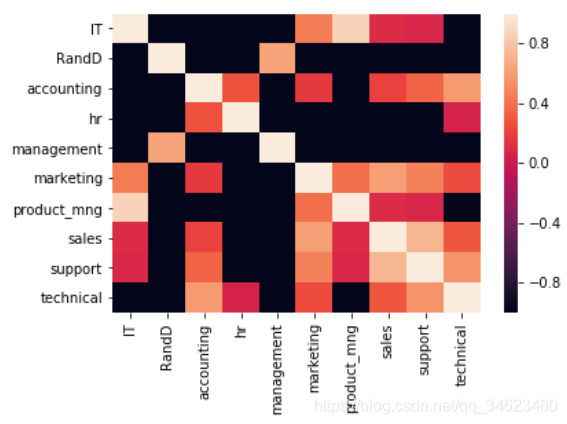
sns.heatmap(dp_t_mat,xticklabels=dp_keys,yticklabels=dp_keys)
plt.show()
#图中颜色越深越接近于0，越接近于0则越表明他们的离职率之间是没有关系的

#交换分析法二——透视表
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

df = pd.read_csv("D:/HR.csv")

#透视表,横坐标：index   列：columns   聚合方法：mean函数
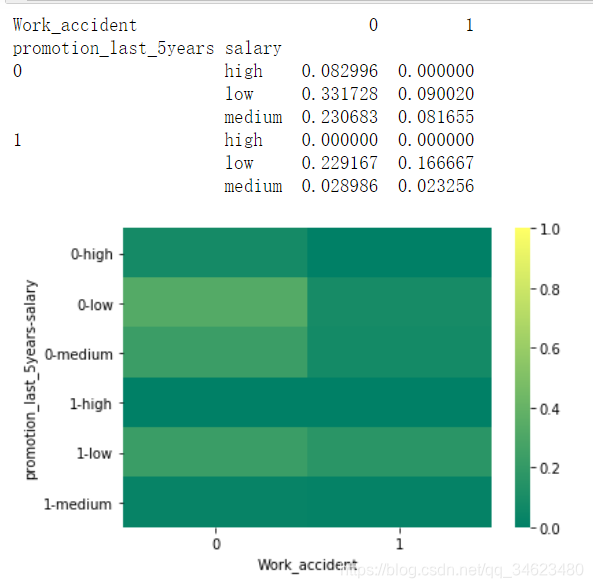
piv_tb=pd.pivot_table(df,values="left",index=["promotion_last_5years","salary"],\
                      columns=["Work_accident"],aggfunc=np.mean)
print(piv_tb)
#过去五年是否有晋升，0代表否，1代表是
#是否有工作事故，0代表否，1代表是
#0.331728最大，表示是过去五年没有工作事故，没有晋升且工资低的容易离职

#指定最大值为1最小值为0
sns.heatmap(piv_tb,vmin=0,vmax=1,cmap=sns.color_palette("summer",n_colors=256))
sns.set_context(font_scale=1.5)
plt.show()
#颜色越浅，离职率越高 

（2）分组分析的含义：①将数据进行分组后，再进行分析比较。
②根据数据的特征将数据进行切分，分成不同的组，使得组内成员尽可能靠拢，组间的成员尽可能远离。那么在这种含义下，如果我们指定了每一条数据的分组，来计算当未知分组的数据出现的时候，更精确地判断它是哪个分组，这个过程我们可以称之为分类。如果我们不知道分组，只是想让数据尽可能的物以类聚，也可以把这个过程叫做聚类。
这里暂时先讨论含义①。分组分析一般与其他分析方法配合在一起使用。从这个角度来看，它更像是一种辅助手段。分组分析最常用手段就是钻取。钻取就是改变数据维度的层次，变换分析力度的过程。
根据钻取方向的不同可以分为向下钻取和向上钻取。
向下钻取就是展开数据，查看数据细节的过程，比如一门考试，每个班都是一个分组。我们知道每个班的平均成绩，如果我们进一步想知道每个班里男生和女生分别平均成绩是多少？这个过程就是向下钻取的过程。
向上钻取就是汇总分组数据的过程。比如我们知道一个品牌汽车每天的销售额，然后汇总成每个月的销售额，以月为单位进行分析。
离散属性的分组是比较容易的，而连续属性的分组在分组前需要进行离散化。当然，在进行连续属性的离散化之前，我们需要先看下数据分布是不是有明显的可以区分的标志，比如将数据从小到大排列的后，有没有一个明显的分隔（相邻两个数据的差即一阶差分）或者明显的拐点（二阶差分）。如果有可以直接使用。另外一个思路，连续属性的分组要尽可能满足相同的分组比较聚拢，不同的分组比较分离的特点。所以我们可以用聚类的方法进行连续属性的分组。比如我们可以用Kmeans方法来进行指定分组数目的连续属性分组，如果考虑标注的话，我们也可以结合不纯度的检验指标（Gini系数）来进行连续数据的离散化分组。
我们先来看衡量不纯度的指标（Gini系数）的计算。


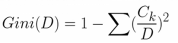
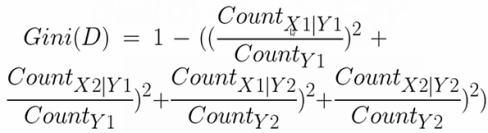
说明：D代表我们目标的标注，C就是相对于我们关注的属性来说要比较和对比的属性。
Count X1|Y1:表示目标标注为Y1时X1有多少个；Count Y1表示Y1的个数。
例：这张表中我们想衡量X相对于Y来说是不是具有很好的区分度。

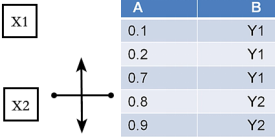
连续值的Gini系数怎么进行计算呢？
我们需要先将表按照连续值（A列）的大小进行排序，然后相邻两两之间划定界限，分别确定分组值。比如这里我们确定X1和X2，然后分别计算Gini系数，取Gini系数最小的切分为界限，这样我们就可以根据目标标注将连续数值进行分组啦。比如我们在0.1_{0.2之间进行一次切分，求它的Gini系数，然后再往下移，再0.2}0.7处再进行一次切分，以此类推。得到的最小值是在0.7~0.8处，从而我们可以在0.75处进行分组。

#分组分析
#在seaborn中绘制柱状图，可以直接的了解它的分组情况
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns


df = pd.read_csv("D:/HR.csv")

#离散值
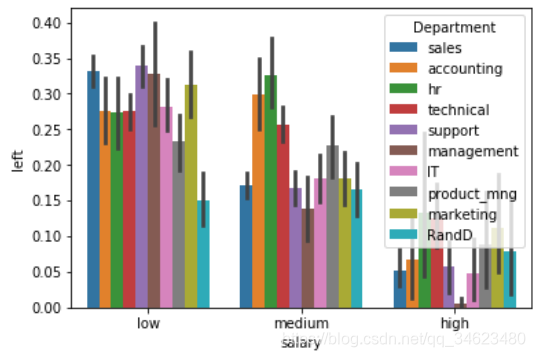
sns.barplot(x="salary",y="left",hue="Department",data=df)
plt.show()
#结果如下图

#连续值
#可以以图中拐弯的点作为分组点
sl_s=df["satisfaction_level"]
sns.barplot(list(range(len(sl_s))),sl_s.sort_values())

（3）相关分析是衡量两组数据或者两组样本变化趋势或者分布趋势变化大小的分析方法。

#相关分析——相关性系数
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

df = pd.read_csv("D:/HR.csv")

#计算相关系数
sns.heatmap(df.corr(),vmin=-1,vmax=1,cmap=sns.color_palette("RdBu",n_colors=128))
plt.show()

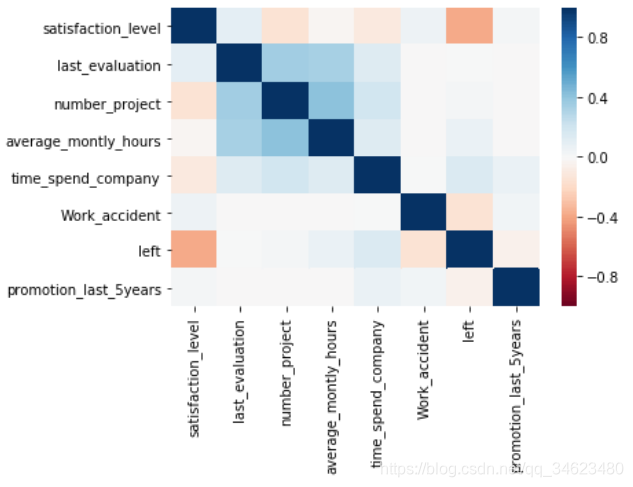
二类离散属性（0、1）的相关性问题：
熵：衡量不确定性。越接近于0，不确定性越小。

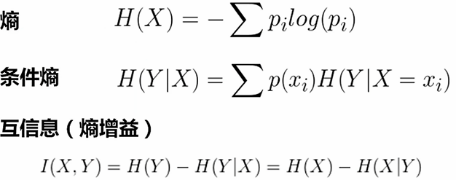
说明：条件熵相对于熵一定是减少的，减少的值就是互信息（熵增益）。
对于分类数目过多的数据，互信息具有不正确的偏向，也就是不具有归一化，它的不确定性是上不封顶的。利用熵增溢率解决此问题。但熵增溢率不具有对称性，利用相关性解决此问题。

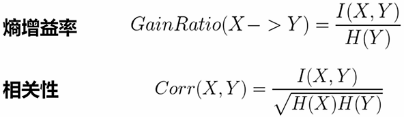
#相关分析——熵
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

s1=pd.Series(["X1","X1","X2","X2","X2","X2"])
s2=pd.Series(["Y1","Y1","Y1","Y2","Y2","Y2"])

#定义熵
def getEntropy(s):
    if not isinstance(s,pd.core.series.Series):
        s=pd.Series(s)
    #计算分布
    prt_ary=pd.groupby(s,by=s).count().values/float(len(s))
    
    return -(np.log2(prt_ary)*prt_ary).sum()

print("Entropy:",getEntropy(s1))
print("Entropy:",getEntropy(s2))
#Entropy: 0.9182958340544896
#Entropy: 1.0


#定义条件熵,条件s1下s2的条件熵
def getCondEntropy(s1,s2):
    #求出s1的分布
    d=dict()
    for i in list(range(len(s1))):
        #构建一个结构体，结构体的key是s1的值
        #它的value是一个数组，数组记录了s1值下s2的分布
        d[s1[i]]=d.get(s1[i],[])+[s2[i]]
    
    return sum([getEntropy(d[k])*len(d[k])/float(len(s1)) for k in d])

print("CondEntropy:",getCondEntropy(s1,s2))
print("CondEntropy:",getCondEntropy(s2,s1))
#由此可以得出条件熵是不对称的(换位置后值不同)
#CondEntropy: 0.5408520829727552
#CondEntropy: 0.4591479170272448

#定义熵增益
def getEntropyGain(s1,s2):
    return getEntropy(s2)-getCondEntropy(s1,s2)

print("EntropyGain:",getEntropyGain(s1,s2))
print("EntropyGain:",getEntropyGain(s2,s1))
#由此可以得出熵增益是对称的
#EntropyGain: 0.4591479170272448
#EntropyGain: 0.4591479170272448

#定义增益率
def getEntropyGainRatio(s1,s2):
    return getEntropyGain(s1,s2)/getEntropy(s2)

print("EntropyGainRatio:",getEntropyGainRatio(s1,s2))
print("EntropyGainRatio:",getEntropyGainRatio(s2,s1))
#由此可以得出增益率是不对称的
#EntropyGainRatio: 0.4591479170272448
#EntropyGainRatio: 0.5

#衡量离散值的相关性度量
import math 
def getDiscreteCorr(s1,s2):
    return getEntropyGain(s1,s2)/math.sqrt(getEntropy(s1)*getEntropy(s2))

print("DiscreteCorr:",getDiscreteCorr(s1,s2))
print("DiscreteCorr:",getDiscreteCorr(s2,s1))
#由此可以得出衡量离散值的相关性度量是对称的
#DiscreteCorr: 0.4791387674918639
#DiscreteCorr: 0.4791387674918639

#Gini系数
def getProbSS(s):
    if not isinstance(s,pd.core.series.Series):
        s=pd.Series(s)
    #计算分布
    prt_ary=pd.groupby(s,by=s).count().values/float(len(s))
    
    return sum(prt_ary**2)

def getGini(s1,s2):
    d=dict()
    for i in list(range(len(s1))):
        d[s1[i]]=d.get(s1[i],[])+[s2[i]]
    
    return 1-sum([getProbSS(d[k])*len(d[k])/float(len(s1)) for k in d])

print("Gini:",getGini(s1,s2))
print("Gini:",getGini(s2,s1))
#Gini: 0.25
#Gini: 0.2222222222222222

6、因子分析（成分分析）

探索性因子分析、验证性因子分析
因子分析，就是从多个属性变量中，分析共性、相关因子的方法。因子分析是个比较综合的分析方法，它几乎用到了我们这一章理论部分所有的知识点。仔细一点讲，因子分析可以分为探索性因子分析和验证性因子分析。探索性因子分析是指通过协方差矩阵，相关性矩阵等指标，分析多元属性变量的本质结构，并可以进行转化、降维等操作，得到数据空间中或者影响目标属性的最主要因子。我们前面讲到的主成分分析法，就是一种比较典型的探索性因子分析方法。验证性因子分析是验证因子与我们关注的属性之间是否有关联，有什么样的关联，是不是符合我们的预期等等。验证性因子分析，常用到我们之前说的假设检验、相关分析、回归分析等等各种理论知识。
举例：比如说我们得到一张数据表，或者得到了非常多的属性，有的时候我们也会得到一个我们关注的目标属性或者标注，比如我们通过问卷调查的方式，可以得到用户对某产品是否满意，还有像年龄、性别等基本信息，还有各种生活习惯等个性的信息。如果我们关注用户对产品的满意情况，我们可以通过主成分分析，把除满意情况外，全部的因子进行主成分降维，然后直接分析降维后因子与满意情况进行对比分析，就是探索性因子分析的一种方法。或者我们也可以不转化，直接来看相关矩阵，看哪一个其他属性和我们关注的属性有比较强的关系，这也是一种探索性因子分析的思路。如果我们换个角度，我们想看一下某具体属性与满意度的关系，我们就不会去验证这个属性和满意度是不是有关系，得到像相关性、一致性之类的指标。或者我们直观上可以猜测某几个指标与满意度有关系，也可以用回归方法去拟合这几个属性与满意度的关联，根据误差大小来应验我们的假设是否准确，这是一种验证性因子分析的思路。

#因子分析（成分分析）——主成分分析
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA

df = pd.read_csv("D:/HR.csv")

#主成分分析
#十个属性去掉三个还剩下七个
my_pca=PCA(n_components=7)
#转化，填入数据表，且不可以有离散型数据，我们关注left，所以它也要去掉
lower_mat=my_pca.fit_transform(df.drop(labels=["left","Department","salary"],axis=1))

#看一下比例
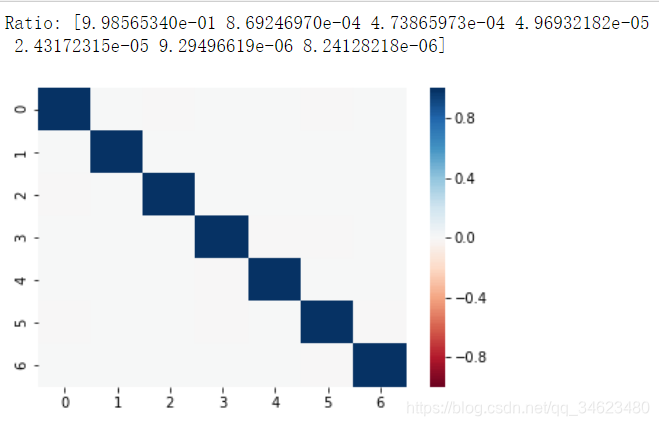
print("Ratio:",my_pca.explained_variance_ratio_)
#可以知道除了第一个，其他的数据都接近于0，所以保留第一个就好了

sns.heatmap(pd.DataFrame(lower_mat).corr(),vmin=-1,vmax=1,cmap=sns.color_palette("RdBu",n_colors=128))
plt.show()
#只有对角线上相关系数几乎为1，其它的几乎为0(主成分不相关)

小结