计算图(computational graph)理解反向传播
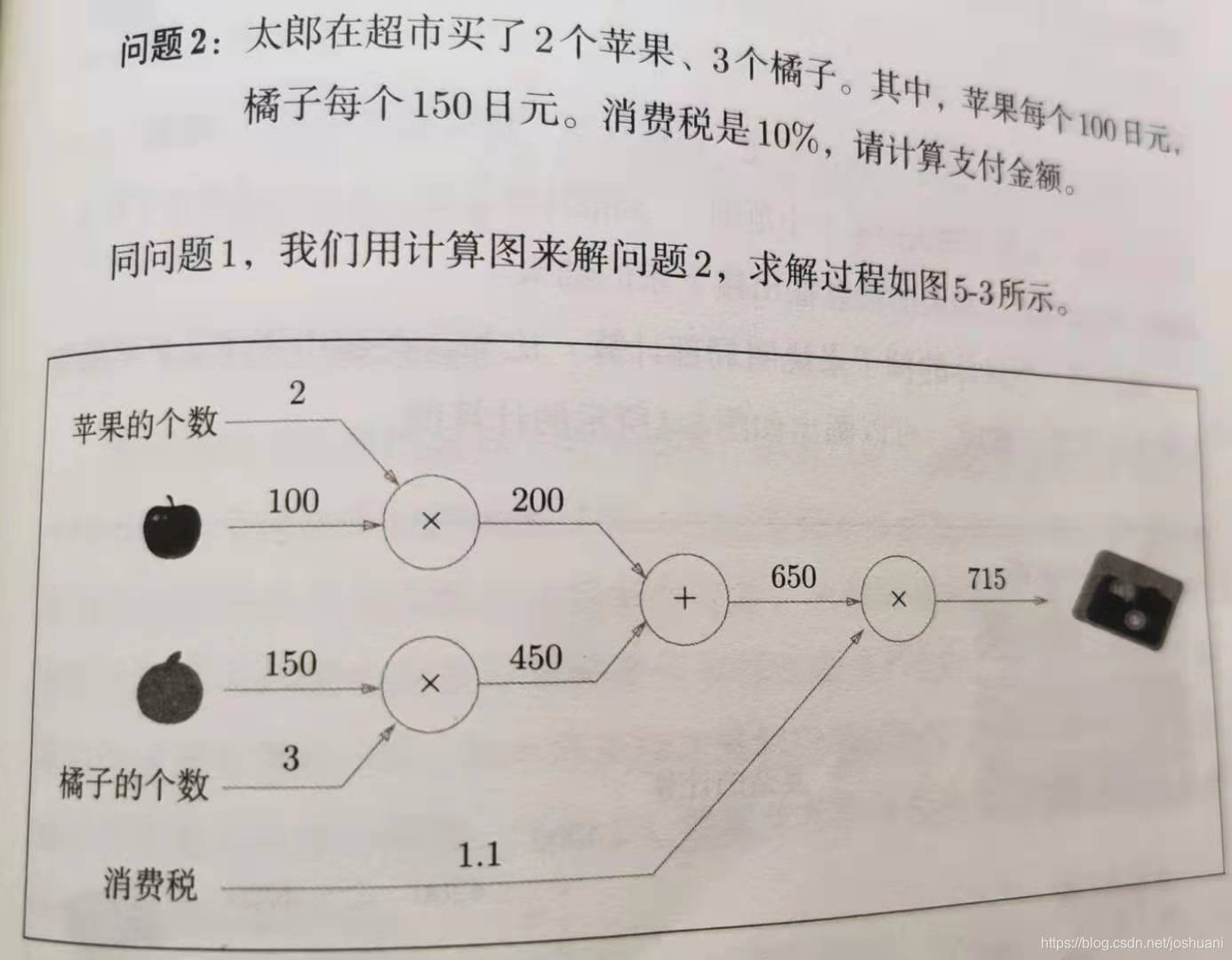
优点:局部计算+可保存中间结果

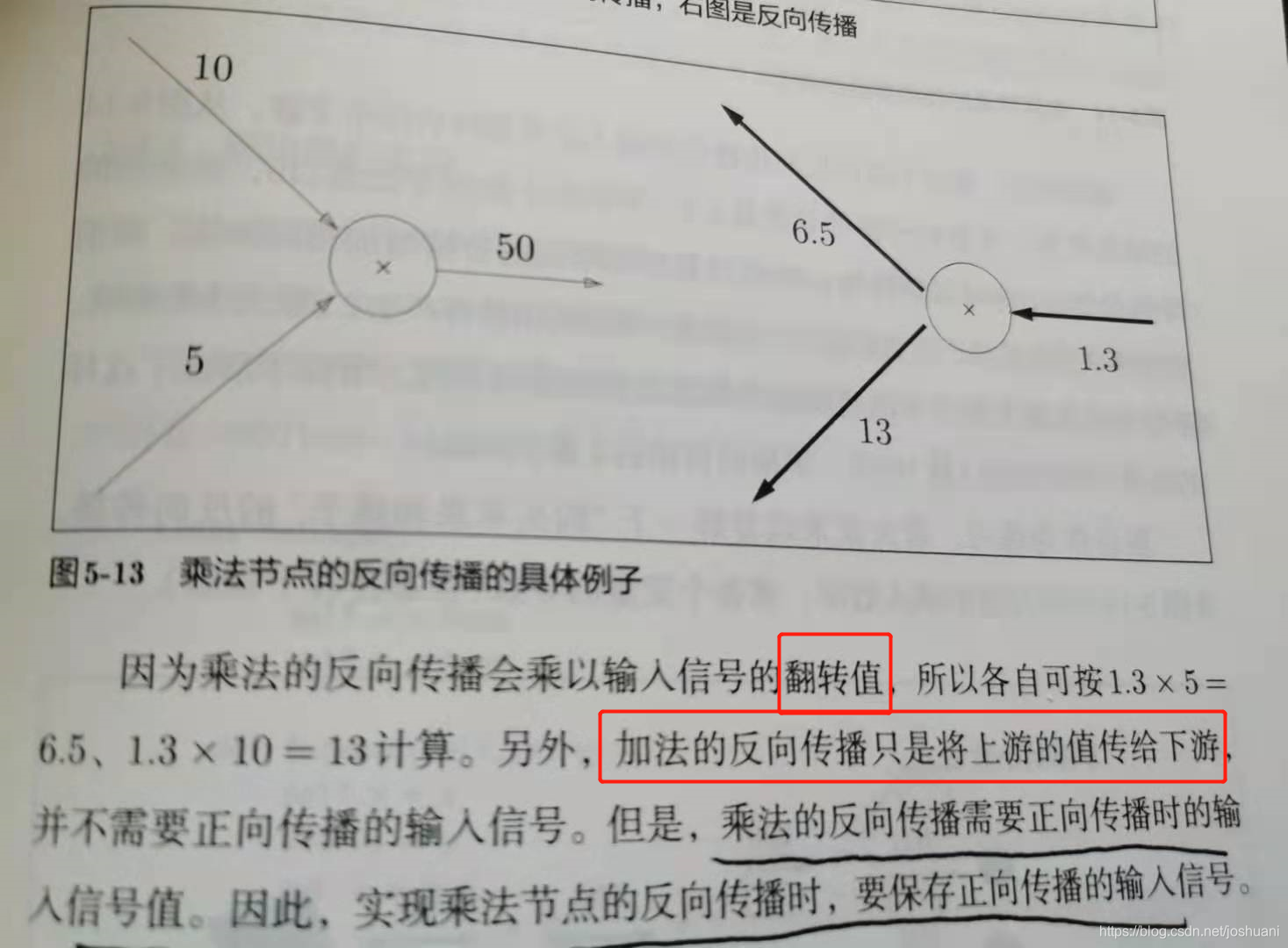

简单层的实现
层是神经网络中的功能单位,包括forward()和backward()->参数dout
乘法层的实现


加法层的实现

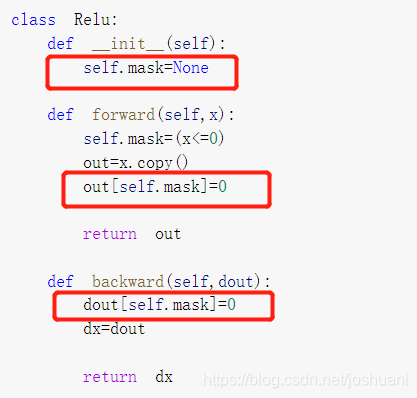
激活函数层的实现
在神经网络层的实现中,一般假定forward() backward()中的参数是Numpy数组。
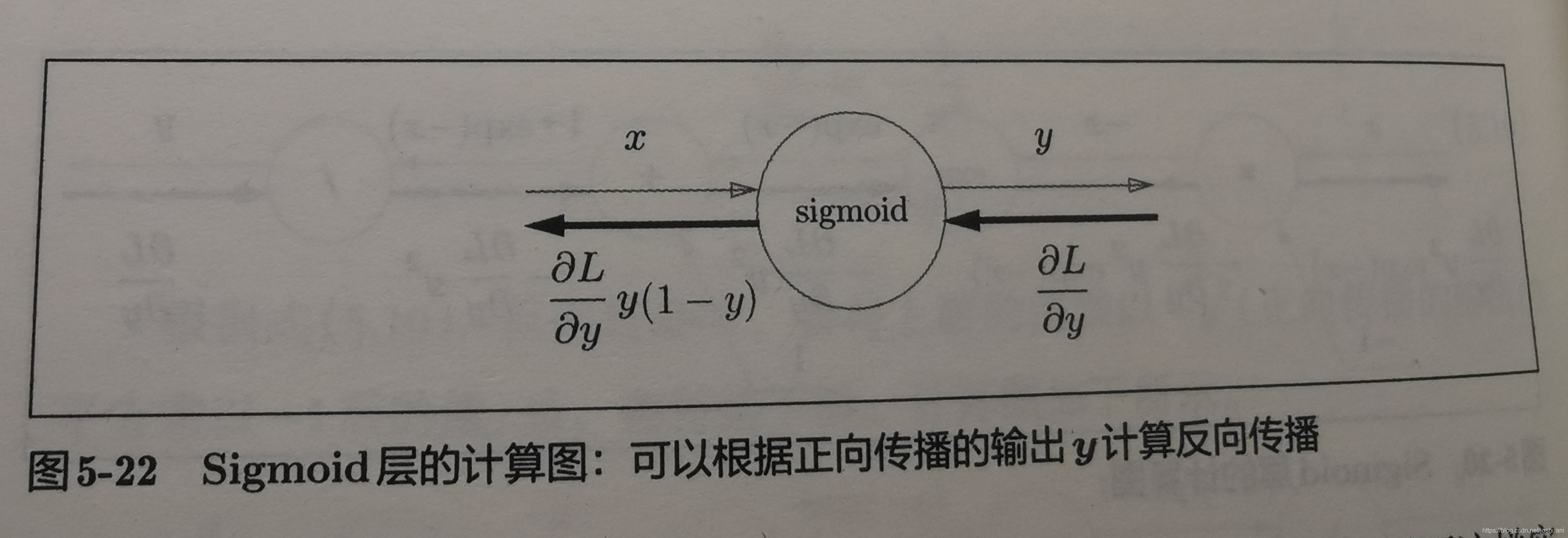
sigmoid层实现


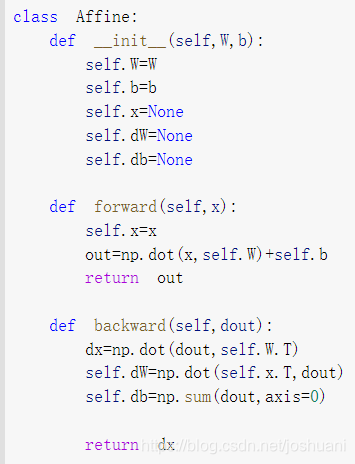
Affine(仿射 即矩阵乘积)层实现

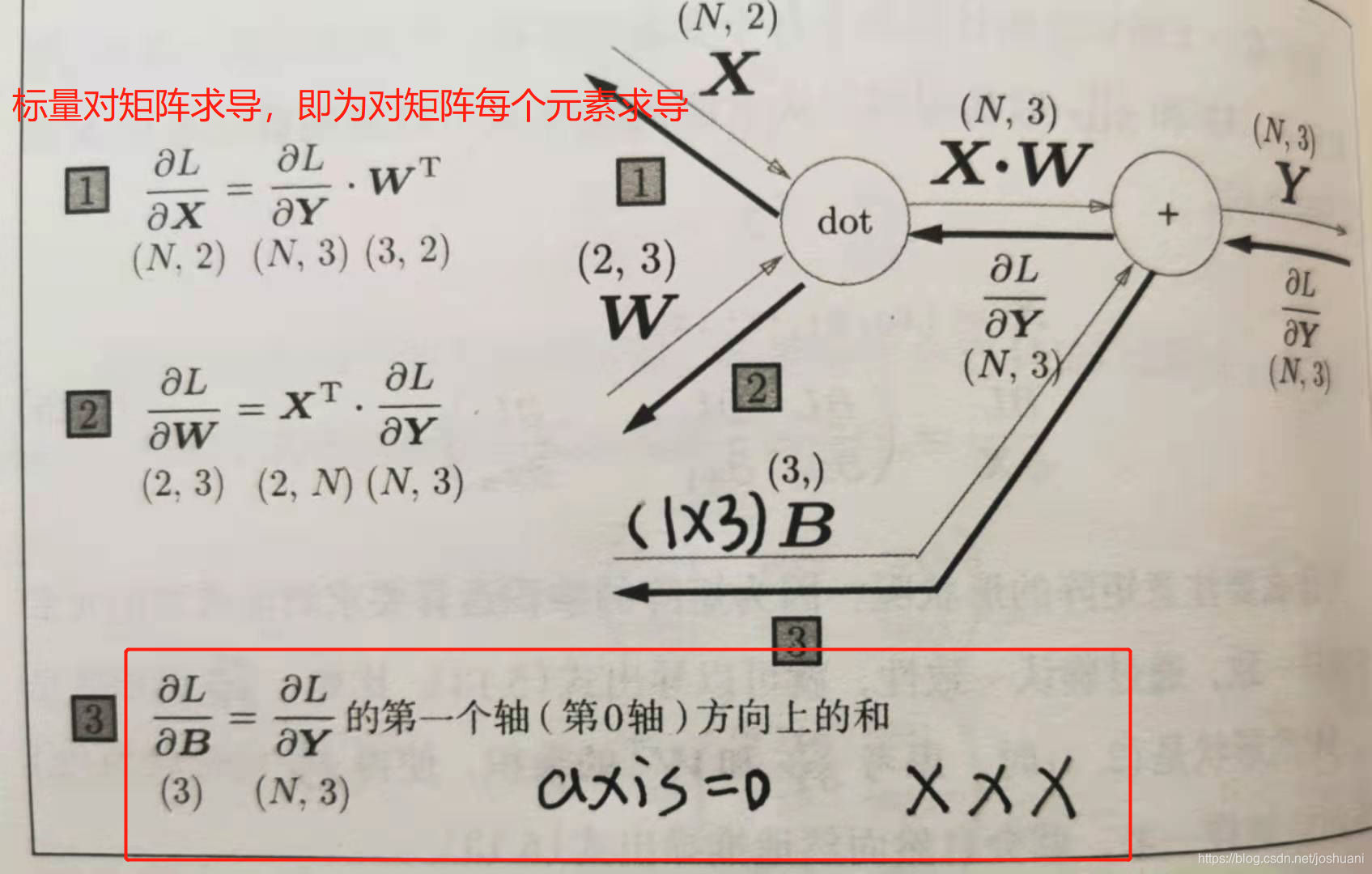
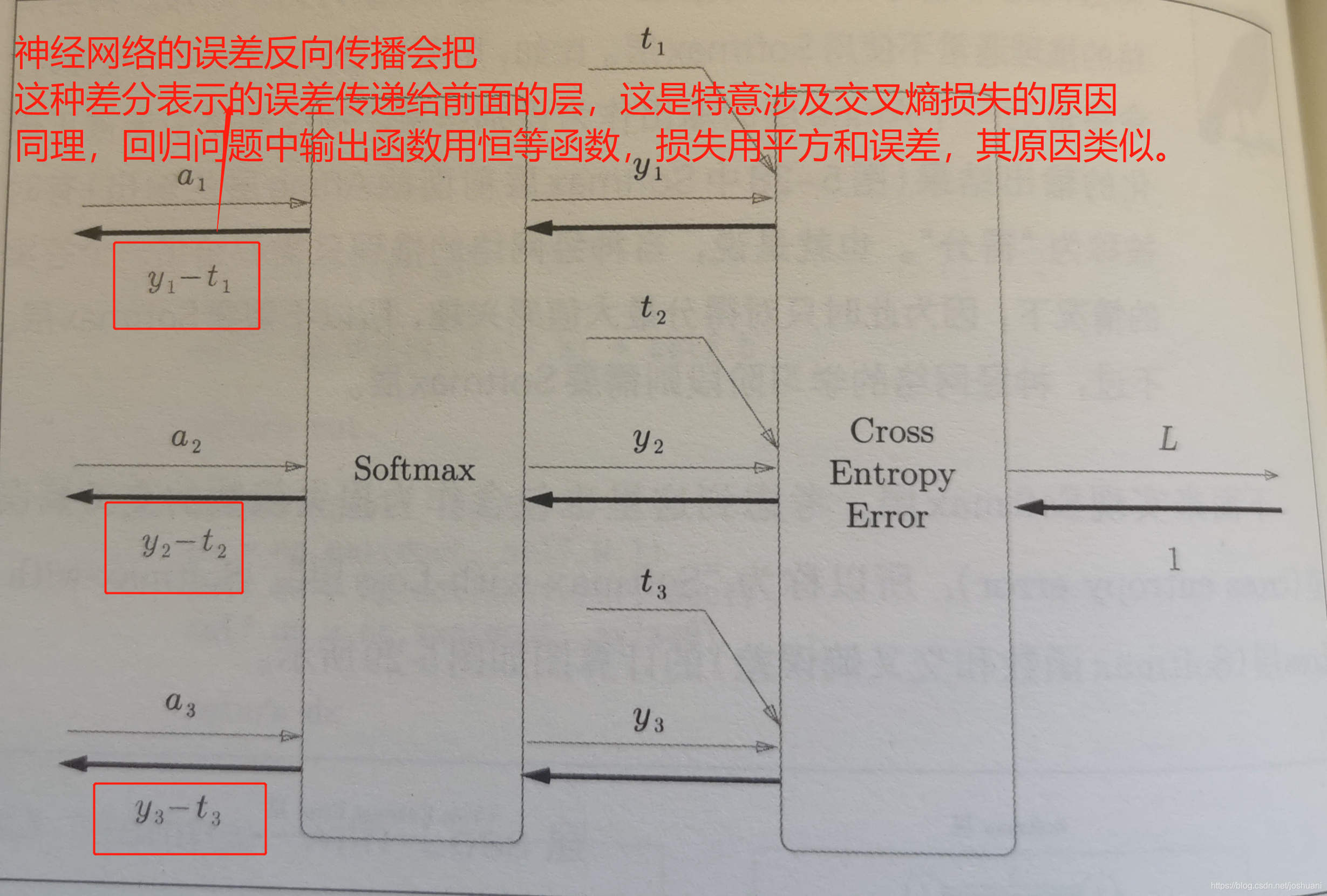
softmax-with-loss层

** 神经网络的推理通常不使用Softmax层,只关注最后一个Affine层的“得分”最大值;学习则需要Softmax层。
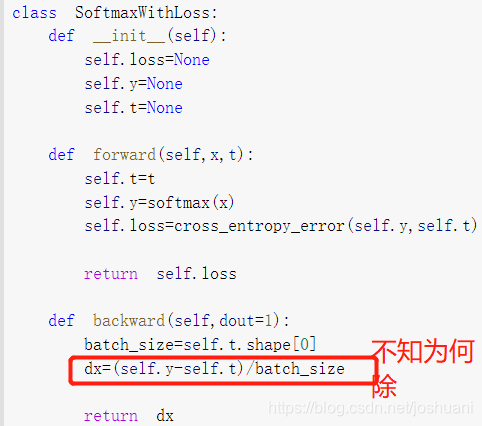
“前向传播中得到的值可以保存 供反向传播算导数用”可以这么理解:层其实是一个类,前向传播的过程其实初始化了数据成员,这就是“保存”的意义,在反向传播的代码里就可以使用已经初始化好的数据成员。
【重要】使用 层+BP的 两层神经网络实现


而之后学习的代码 求梯度就用BP 然后梯度下降
梯度确认(gradient check)
数值微分很慢,但实现简单不宜错
BP快但容易错
梯度确认:确认数值微分得出的结果和误差反向传播求得的结果是否一致(其实是非常相近)