常用优化算法

Gradient Descent梯度下降

在梯度下降中，每进行一次更新需要遍历整个数据集，以求得梯度大小。这会大大的增加运行的时间。为解决这个问题，因此有了SGD。

Stochastic Gradient Descent(SGD)随机梯度下降

SGD算法，每次随机选择一个样本计算梯度来进行迭代，随机梯度是对梯度的一个无偏估计。
缺点：（1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。（2）可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。

Mini Batch Gradient Descent小批量随机梯度下降

在随机梯度下降中每次迭代只随机采样一个样本计算梯度。在小批量随机梯度下降中，我们则在每轮迭代中随机采样多个样本，用这个小批量样本计算梯度。

使用小批量梯度下降的优点是：

可以减少参数更新的波动，最终得到效果更好和更稳定的收敛。
还可以使用最新的深层学习库中通用的矩阵优化方法，使计算小批量数据的梯度更加高效。

动量法

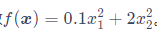
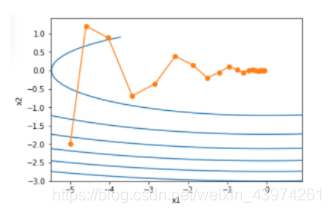
在这里插入图片描述

当目标函数为一个二维函数，不同变量的系数不同，会导致梯度下降时系数较大方向上的变量变化更大。
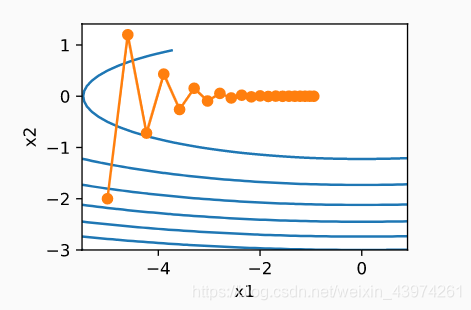
在这里插入图片描述
上图x2方向的变换更明显，为了减小x2变化幅度，为了解决这个问题，提出了动量法。
动量法的原理如下图：

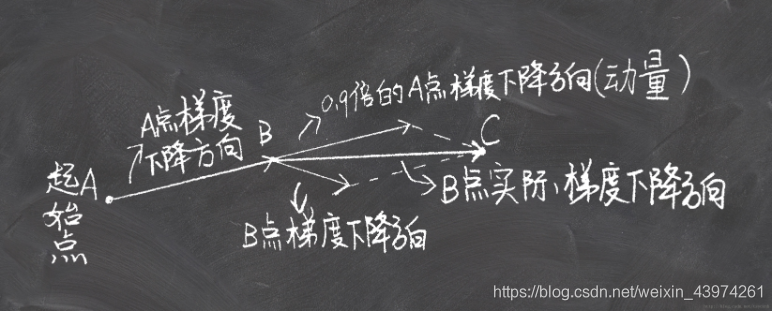
主要是在B点出的梯度下降方向加上一个自变量gama乘以A点的梯度下降方向，就可以得到B点实际的下降方向，通过这个办法可以有效地减少x2的变化幅度。（假如A点和B点梯度方向相反，加起来就刚好可以抵消）

θ 为参数，α 为学习率，vt为速度变量。
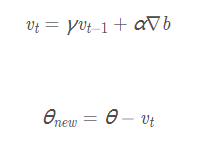
在这里插入图片描述
使用动量法后的图像能明显看出比之前缓和。

指数加权移动平均（EWMA ）

指数加权移动平均是动量法的主要思想。
指数移动加权平均法，是指各数值的加权系数随时间呈指数式递减，越靠近当前时刻的数值加权系数就越大。
在计算机中，它相较于普通的平均的优点是：1.不用保存所有的数值。2.显著减小计算量。
下图是美国每天的温度变化情况。
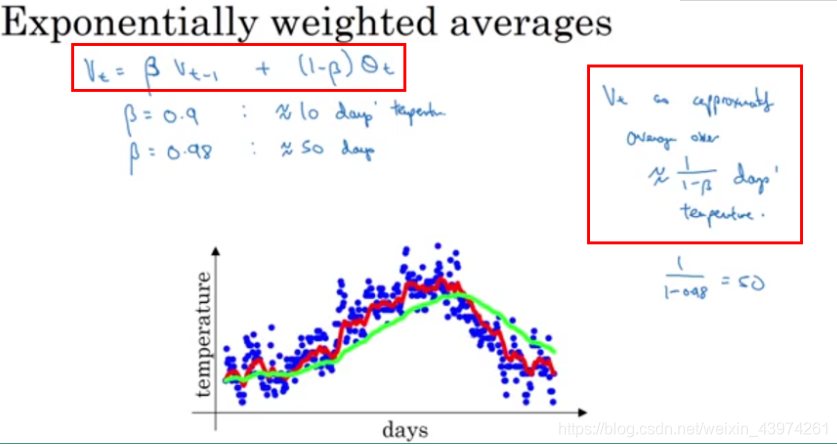
在这里插入图片描述
EWMA 的表达式如下：

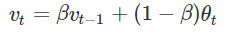
上式中 θt 为时刻 t 的实际温度；系数 β 表示加权下降的速率，其值越小下降的越快；vt 为 t 时刻 EWMA 的值。

在上图中有两条不同颜色的线，分别对应着不同的 β 值。

当 β=0.9 时，对应着图中的红线，此时虽然曲线有些波动，但总体能拟合真实数据。
　　当 β=0.98 时，对应着图中的绿线，此时曲线较平，但却有所偏离真实数据。
在这里插入图片描述
从上式可以看出越早的参数的系数越小。在数学中一般会以 1/e 来作为一个临界值，小于该值的加权系数的值不作考虑，接着来分析上面 β=0.9 和 β=0.98 的情况。

当 β=0.9 时，0.9的10次方约等于 1/e ，因此认为此时是近10个数值的加权平均。

当 β=0.98 时，0.98的50次方约等于 1/e，因此认为此时是近50个数值的加权平均。

修正偏差

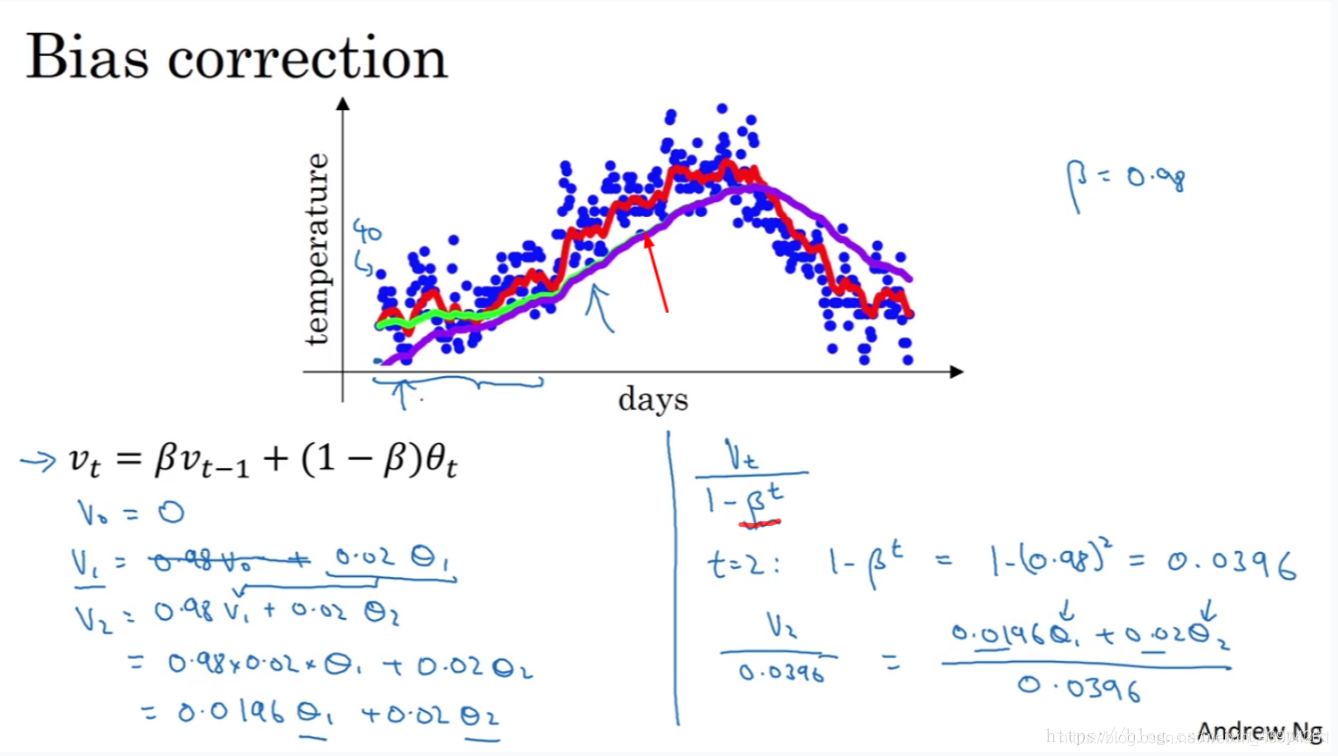
在这里插入图片描述
从图中可以看紫线和绿线，都是 β=0.98时的图像。绿线是理论值，紫色是实际得到的值。在开始时紫线的起始点更低，这是由于v0等于0，初始化的值太小。通过对公式做一些修改：

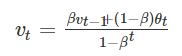
当 t 很小时，分母可以很好的放大当前的数值；当 t 很大时，分母的数值趋于1，对当前数值几乎没有影响。

AdaGrad算法

动量法里我们看到当x1,x2 的梯度值有较大差别时，需要选择足够小的学习率使得自变量在梯度值较大的维度上不发散。但这样会导致自变量在梯度值较小的维度上迭代过慢。动量法依赖指数加权移动平均使得自变量的更新方向更加一致，从而降低发散的可能。
AdaGrad算法，它根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率，从而避免统一的学习率难以适应所有维度的问题。

在这里插入图片描述

需要强调的是，小批量随机梯度按元素平方的累加变量st出现在学习率的分母项中。因此，如果目标函数有关自变量中某个元素的偏导数一直都较大，那么该元素的学习率将下降较快；反之，如果目标函数有关自变量中某个元素的偏导数一直都较小，那么该元素的学习率将下降较慢。
缺点：由于st 一直在累加按元素平方的梯度，自变量中每个元素的学习率在迭代过程中一直在降低（或不变）。所以，当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。