第1章绪论

1.1 模式和模式识别的概念

能用自己的语言解释相关名词（模式、模式识别、样本、特征、模式类）

能举例说明模式识别系统中的相关内容

模式：对客体（研究对象）特征的描述（定量的或结构的描述），是取自客观世界的某一样本的测量值的集合（或综合）。

模式识别：确定一个样本的类别属性（模式类）的过程，即把某一样本归属于多个类型中的某个类型。

样本：一个具体的研究（客观）对象。如患者，某人写的一个汉字，一幅图片等。

特征：能描述模式特性的量（测量值）。在统计模式识别方法中，通常用一个矢量x表示，称之为特征矢量，记为
$\vec x = (x_1,x_2,...x_n)'$
模式类：具有某些共同特性的模式的集合。

1.2 模式识别系统

能画出模式识别系统框图

能用自己的语言描述模式识别系统各部分的功能

能举例说明模式识别系统

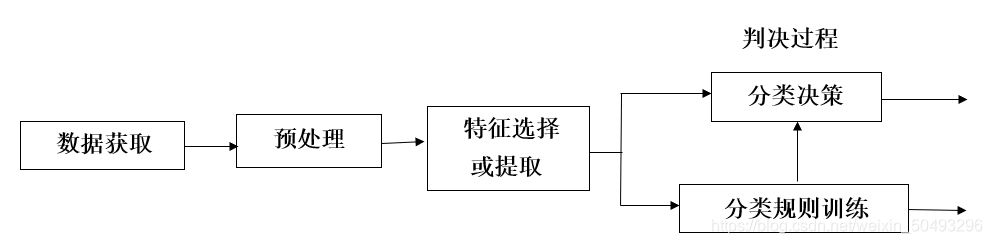
在这里插入图片描述

功能

数据获取模块：用数字符号来表示所研究的对象
预处理模块：
- 去噪声。去掉不相关的信息，提取有用信息
- 数据完善。对输入测量仪器或其它因素所造成的退化现象进行复原
特征提取和选择：对原始数据进行变换，得到最能反映分类本质的特征
分类决策：在特征空间中用模式识别方法把被识别对象归为某一类别
分类规则训练：通过对样本的学习，调节分类规则中的参数

1.3 模式识别概述

能用自己的语言描述按理论分类的模式识别系统，并指出他们的差异

能用自己的语言描述按实现分类的模式识别系统，并指出他们的差异

按理论分类的模式识别系统

统计模式识别：采用概率论和数理统计的方法。采用判别函数，使得误判概率最小
句法模式识别：对模式的结构进行分析：先将模式表示为基元，再分析基元构成的句法结构
模糊模式识别：以隶属度
为基础，运用模糊数学中的“关系”概念和运算进行分类
神经网络模式识别：以人工神经元为基础，模拟人脑神经细胞的工作特点。对脑部工作的生理机制进行模拟，实现形象思维的模拟

按实现方法分类的模式识别系统

监督（有人管理）分类
- 利用判别函数进行分类判别。需要有足够的先验知识
非监督（无人管理）分类
- 用于没有先验知识的情况下，通常采用聚类分析的方法

1.4 模式识别的应用

了解宏观领域的模式识别应用

了解生物识别的模式识别应用

补充模式识别的数学基础

了解特征矢量和特征空间的概念

了解随机矢量的定义和描述

会进行基本的矩阵运算

特征矢量：设一个研究对象的n个特征量测量值（如鱼的长度、光泽度）分别为X1,…,Xn，我们将其作为一个整体来考虑，则他们构成一个n维特征矢量x
特征空间：各种不同取值的特征矢量的全体构成n维特征空间
特征矢量是特征空间的一个点
随机变量：如果特征分量的每次观测值都不确定，则该特征分量为随机变量
随机矢量：若特征矢量的每个特征分量都是随机变量，则称其为随机矢量
随机矢量的描述
- 分布函数
设X=(X1,X2,…,Xn)'为随机矢量，x=(x1,x2,…,xn)'为确定性矢量

随机矢量的联合概率分布函数定义为：
$F(x_1,x_2,...,x_n)=P(X_1≤x_1,X_2≤x_2,...,X_n≤x_n)\\ F(\vec x)=P(\vec X ≤\vec x)$
式中P(.)表示括号中事件同时发生的概论

解释：分布函数就是随机矢量X落在区域X<x内的概论
- 概率密度函数
随机矢量X的联合概率密度函数定义为：
$p(x_1,x_2,...,x_n)=p(\vec x)=\partial F(x_1,x_2,...,x_n)/\partial x_1\partial x_2...\partial x_n$
解释：概率密度函数是分布函数的导数，相当于单位区域内的概率

对比：质量、密度、体积 vs 分布函数、概率密度函数、区域
- 数字特征
  - 均值矢量（期望矢量）
    
    n维随机矢量X的均值矢量
    定义为：
    $\vec \mu=E[\vec x]=(E[X_1],...,E[X_n])^T=\int_{X^n}\vec xp(\vec x)d\vec x$
    说明：
    
    1. 矢量的均值为每个分量的均值
    
    2. 每个分量的均值为概率乘以取值的积分
  - 协方差矩阵
    
    随机矢量X的协方差矩阵表征各分量围绕其均值的散布情况及各分量间的相关关系，定义为：
  - 自相关矩阵
    
    随机矢量X的自相关矩阵定义为：
    $R=E[\vec X\vec X^T]$
    协方差矩阵与自相关矩阵的关系为：
    $\sum=R-\vec \mu\vec \mu^T$
    自相关矩阵去掉均值因素就是协方差矩阵
  - 相关系数
    
    随机矢量X的相关系数定义为：
    $r_{ij}=\sigma_{ij}^2/(\sigma_{ii}\sigma_{jj})$
    由布尼亚科夫斯基不等式知
    $|\sigma_{ij}^2|≤\sigma_{ii}\sigma_{jj}\\ 故-1≤r_{ij}≤1$
    相关系数矩阵定义为：
    $r=(r_{ij})_{n×n}\\ 当\sigma_{ij}^2=0时，r_{ij}=0,X的第i个分量X_i和第j个分量X_j不相关，\\ 此时E[X_iX_j]=E[X_i]E[X_j]$
  - 不相关
    $随机矢量\vec X与\vec Y不相关的充要条件是互协方差矩阵为0：\\ cov(\vec X,\vec Y)=0,即E[\vec X\vec Y^T]=E[\vec X]E[\vec Y^T]$
  - 正交
    $随机矢量\vec X与\vec Y若满足E[\vec X\vec Y^T]=0，则称\vec X与\vec Y正交$
  - 独立
    $随机矢量\vec X与\vec Y的联合概率密度函数p(\vec x,\vec y)若满足\\ p(\vec x,\vec y)=p(\vec x)p(\vec y)\\ 则称\vec X与\vec Y独立$
正态分布

正态分布的一维随机变量X的概率密度函数为
$p(x)=\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{(x-\mu)^2}{2\sigma^2}]\\ 其中，\mu为数学期望，\sigma^2为方差\\ \mu=E[X]=\int_{-\infty}^{+\infty}xp(x)dx\\ \sigma^2=E[(X-\mu)^2]=\int_{-\infty}^{+\infty}(x-\mu)^2p(x)dx\\ 正态分布随机矢量\vec X=(X_1,X_2,...,X_n)'的概率密度函数定义为：\\ p(x_1,x_2,...,x_n)=p(\vec x)=\frac{1}{(2\pi)^{n/2}|\sum|^{1/2}}exp[-\frac{1}{2}(\vec x-\vec \mu)'{\sum}^{-1}(\vec x-\vec \mu)]\\ 其中，\vec \mu=E[\vec X]=(E[X_1,...,E[X_n]])为X的数学期望矢量，\sum为X的协方差矩阵\\ \sum=E[(\vec X-\vec \mu)(\vec X-\vec \mu)']=\begin{pmatrix} {\sigma_{11}^2}&{\sigma_{12}^2}&{\cdots}&{\sigma_{1n}^2}\\ {\sigma_{21}^2}&{\sigma_{22}^2}&{\cdots}&{\sigma_{2n}^2}\\ {\vdots}&{\vdots}&{}&{\vdots}\\ {\sigma_{n1}^2}&{\sigma_{n2}^2}&{\cdots}&{\sigma_{nn}^2}\\ \end{pmatrix}$
性质
- $分布函数完全由\vec \mu和\sum确定$
- 不相关等价于独立
- 正态分布随机矢量的线性变换仍为正态随机矢量
计算向量的内积
$设任意两个n维向量X=\{x_1,...,x_n\},Y=\{y_1,...,y_n\},其内积为(X,Y)=\sum_{i=1}^nx_iy_i$
计算向量的外积
$为简单起见，设任意两个3维向量X=\{x_1,x_2,x_3\},Y=\{y_1,y_2,y_3\},\\ 其外积为A=\begin{pmatrix} {x_1}\\ {x_2}\\ {x_3}\\ \end{pmatrix} \begin{pmatrix} {y_1}&{y_2}&{y_3} \end{pmatrix}=\\ \begin{pmatrix} {x_1y_1}&{x_1y_2}&{x_1y_3}\\ {x_2y_1}&{x_2y_2}&{x_2y_3}\\ {x_3y_1}&{x_3y_2}&{x_3y_3}\\ \end{pmatrix}$
计算微商
$设任意两个n维向量X=\{x_1,...,x_n\},Y=\{y_1,...,y_n\},矩阵A=(a_{ij})_{n×n},和标量k,则\\ \frac{dX}{dk}= \begin{pmatrix} {\frac{\partial x_1}{\partial k}}\\ {...}\\ {\frac{\partial x_n}{\partial k}} \end{pmatrix}, \frac{dk}{dX}= \begin{pmatrix} {\frac{\partial k}{\partial x_1}}\\ {...}\\ {\frac{\partial k}{\partial x_n}} \end{pmatrix}, \frac{dk}{dA}= \begin{pmatrix} \frac{\partial k}{\partial a_{ij}} \end{pmatrix}_{n×n}, \frac{dX}{dY}= \begin{pmatrix} {\frac{\partial x_1}{\partial y_1}}&{\frac{\partial x_1}{\partial y_2}}&{\cdots}&{\frac{\partial x_1}{\partial y_n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {\frac{\partial x_n}{\partial y_1}}&{\frac{\partial x_n}{\partial y_2}}&{\cdots}&{\frac{\partial x_n}{\partial y_n}} \end{pmatrix}$
计算矩阵的迹
$n阶矩阵A的主对角线上各元素之和称为A的迹，记作tr(A)=\sum_{i=1}^{n}a_{ii}$
计算矩阵的行列式

$矩阵A=(a_{ij})_{n×n}的行列式为D=\sum_{i=1}^na_{1i}A_{1i}，其中A_{1i}为a_{1i}的代数余子式\\ 代数余子式的计算方法为：\\ 划去a_{ij}所在的行和列的元素，余下元素构成的行列式叫做a_{ij}的余子式，记作M_{ij}，将\\(-1)^{i+j}M_{ij}=A_{ij}叫做元素a_{ij}的代数余子式$

计算矩阵的逆矩阵
$求逆矩阵：A^{-1}=\frac {1}{|A|}A^*\\ |A|——A的行列式\\ A^*——A的伴随矩阵\\ 若A= \begin{bmatrix} {a_{11}}&{a_{12}}&{a_{13}}\\ {a_{21}}&{a_{22}}&{a_{23}}\\ {a_{31}}&{a_{32}}&{a_{33}}\\ \end{bmatrix},则A^*= \begin{bmatrix} {A_{11}}&{A_{21}}&{A_{31}}\\ {A_{12}}&{A_{22}}&{A_{32}}\\ {A_{13}}&{A_{23}}&{A_{33}}\\ \end{bmatrix}\\ A_{ij}是a_{ij}的代数余子式，注意两者的行和列的标号互换$
计算矩阵的特征值和特征向量
$设A=(a_{ij})_{n×n}是n阶矩阵，若对于数\lambda,存在n维非零向量X，使得AX=\lambda X成立，\\则称\lambda为A的一个特征值,X称为A的属于特征值\lambda的特征向量$
- 计算特征值
  $计算下列行列式即可求解特征值\lambda： \begin{vmatrix} {\lambda-a_{11}}&{\cdots}&{-a_{1n}}\\ {\vdots}&{\ddots}&{\vdots}\\ {-a_{n1}}&{\cdots}&{\lambda-a_{nn}} \end{vmatrix}=0$
- 计算特征向量
  $解方程(\lambda I-A)X=0即可得特征向量X$