3.1-3.6 小节
解析解:损失函数形式较为简单,误差最小化的问题可以直接用公式表达出来。
数值解(多数情况):没有解析解,只能通过优化算法有限次迭代模型来尽可能降低损失函数的值。
小批量随机梯度下降(最常用):先随机选取一组模型的初始值,然后对参数进行多次迭代,每次迭代都有可能降低损失函数的值。具体过程是:随机采样一个固定数目的小批量,然后求小批量中数据样本的平均损失有关模型参数的导数,就是梯度,最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。
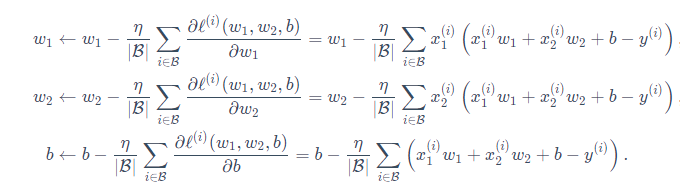
超参数:批量大小和学习率,不是训练得到的,是认为设定的,需要反复试错来找到合适的超参数。
在优化算法停止时的值,不一定是最优解,是对最优解的一个近似。
输出层中的神经元和输入层中各个输入完全连接,叫做全连接层或者稠密层。
线性回归从零开始实现中,如下图中,对loss求和,因为它原来是一个张量,在求梯度的时候肯定要求和,也相当于传入了一个和输入张量大小一样的张量。

self相关:

学习率相关:
定义优化器,对于网络的可学习参数,设置学习率。

还可以对网络的不同子网络设置不同的学习率,在网络微调的时候经常用到。

不让学习率固定成一个常数,调整学习率,可以直接修改优化器中参数里的学习率。也可以新建一个优化器,但是对于使用动量的优化器,新建时,会丢失动量信息,所以一般都调整。
注意在训练模型过程中,先梯度清零,再 计算梯度,再进行反向传播。

线性回归简洁实现中,数据加载方式。这里将torch.utils.data设置名字为Data,后面那个分类任务里是直接写了那一串。
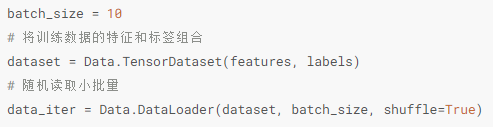
先是把所有的数据装进来,特征和标签结合,然后进行数据加载,随机读取小批量,可以对数据进行打乱。
线性回归输出是连续值,softmax输出是离散值,适合分类问题。
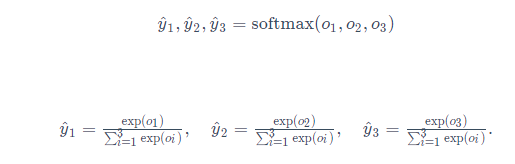
线性回归损失函数是均方误差,softmax回归是交叉熵损失函数,这两个都是单层的神经网络呢。
torchvision是计算机视觉上用的一个包,也就是图像相关的,一些常见模块如下。

python中_作为变量名多为临时变量
在进行小批量数据读取过程中,可以使用多进程来加速数据读取。
softmax回归从零实现:
使用小批量计算时,输出的是一个矩阵,一个维度是batch的大小,一个维度就是类别的维度,单看一个样本是几类就是几类,然后计算每个类别的概率。
对多维数组按维度操作,就是对一个二维矩阵,可以对其中一行或者一列求和,并且保留行和列这两个维度。通过(keepdim=True)

输出

softmax运算过程:输入矩阵,行数是样本数也就是batch数,列数是输出个数,也就是类别,具体计算过程是先对每个元素做指数运算,然后对矩阵的同行元素求和,然后每行各元素和该行元素之和相除,得到最终矩阵,每行之和为1

随机输入,然后进行softmax操作,得到输出


这里最后输出的和[1.,1.]是求和之后维度被压缩了,没有保持二维。
定义softmax回归模型,使用view函数将原始图像改成向量,然后构建模型。

定义损失函数,先使用gather函数得到两个样本标签的预测概率。标签类别也是从0开始的。

上图的过程是两个样本的预测概率,是一个矩阵,实际标签是y,先将标签的一维张量变成列的,然后预测的是矩阵,第一行是第一个样本的,对应实际值的0,也就是提取了实际标签的概率值0.1,然后第二个样本提取了标签为2的概率值,最终输出。

然后实现交叉熵损失函数,这里得到结果是一个向量,表示每个样本的交叉熵的值。
计算分类准确率过程,

返回每行中最大元素的索引,第一行返回2,第二行返回2,然后实际标签分别是0,2,然后再使用float转换,相等转换为1,不相等转换为0,总数目就是样本数,值为1的就是相等,所以可以计算均值然后提取数,得到最终准确率。
评估模型在数据集上的准确率,可以将此过程封装在函数里,

这里计算了求和,是预测标签和实际标签相等的数量,然后不断累加,除以总样本数,得到整个数据集的准确率。

训练模型的过程,优化器就是执行梯度下降的一些设置,比如sgd随机梯度下降,在每一次迭代中,也就是一个batch中,要先梯度清零,然后再计算梯度,反向传播。
几个函数:
- iter(object) 用来生成迭代器,参数是支持迭代的集合对象,返回迭代器对象,
- zip()函数,将可迭代对象作为参数,将对象中对应的元素打包成一个个元组,返回由这些元组组成的列表。
- next()函数,返回迭代器的下一个项目,要和生成迭代器的iter()函数一起使用。一次获得一个下一个项目。