文章目录
1. Logistic Regression
1.1 Logistic Regression & Perceptron
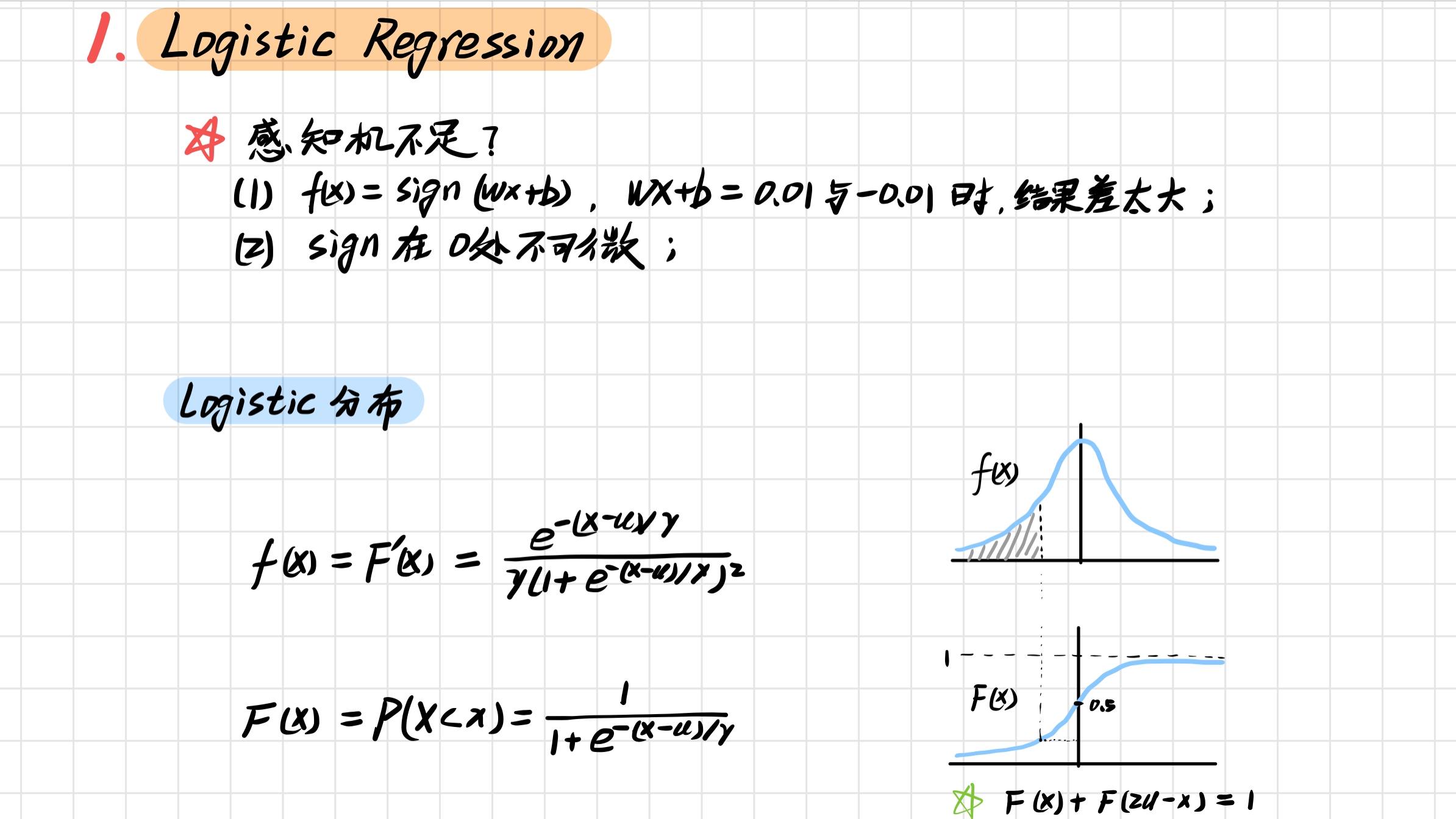
1.2 Logistic 回归模型的定义

1.3 最大似然估计估计模型参数

总结

2. Logistic 回归的 Python 实现
2.1 数据集
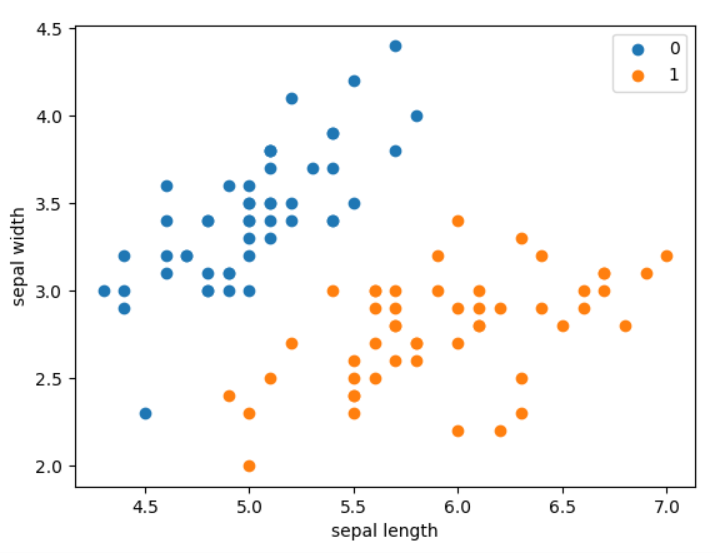
数据集为鸢尾花数据集,包含两种类型的花,每个样本包含两个特征和一个类别,设置测试集与训练集的比例为 1 : 4:
from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def create_data():
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sl', 'sw', 'pl', 'pw', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
return data[:, [0, 1]], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
plt.scatter(X[:50, 0], X[:50, 1], label='0')
plt.scatter(X[50:, 0], X[50:, 1], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()
结果如下:
2.2 构建模型
接着我们构建 LogisticRegressionClassifier 的 model:
class LogisticRegressionClassifier:
# 最大迭代次数和学习步长
def __init__(self, max_iter=200, learning_rate=0.01):
self.max_iter = max_iter
self.learning_rate = learning_rate
def sigmoid(self, x):
return 1 / (1 + exp(-x))
def expand(self, X):
matrix = []
for item in X:
matrix.append([*item, 1.0])
return matrix
def fit(self, X, y):
X = self.expand(X)
self.weights = np.zeros((len(X[0]), 1), dtype=np.float32) # columnn matrice
for iter_ in range(self.max_iter):
for item_x, item_y in zip(X, y):
res = self.sigmoid(np.dot(item_x, self.weights))
self.weights += self.learning_rate * (item_y - res) * np.transpose([item_x])
print(f'LogisticRegression Model(learning_rate={self.learning_rate}, max_iter={self.max_iter}')
def score(self, X_test, y_test):
success = 0
expanded_X = self.expand(X_test)
for X, y in zip(expanded_X, y_test):
predict_res = np.dot(X, self.weights) > 0.5
if predict_res == y:
success += 1
return success / len(X_test)
说明
(1) 注意到,sigmoid 函数使用的为 exp(-x) ,因为使用 exp(x) 有可能出现溢出 !
(2) expand 函数对 X 进行扩展,增加一个 1
(3) 拟合函数 fit() 类似感知机,它的原理为 最大似然估计 求参数,可以使用 随机梯度 计算极大值,原理 如下:
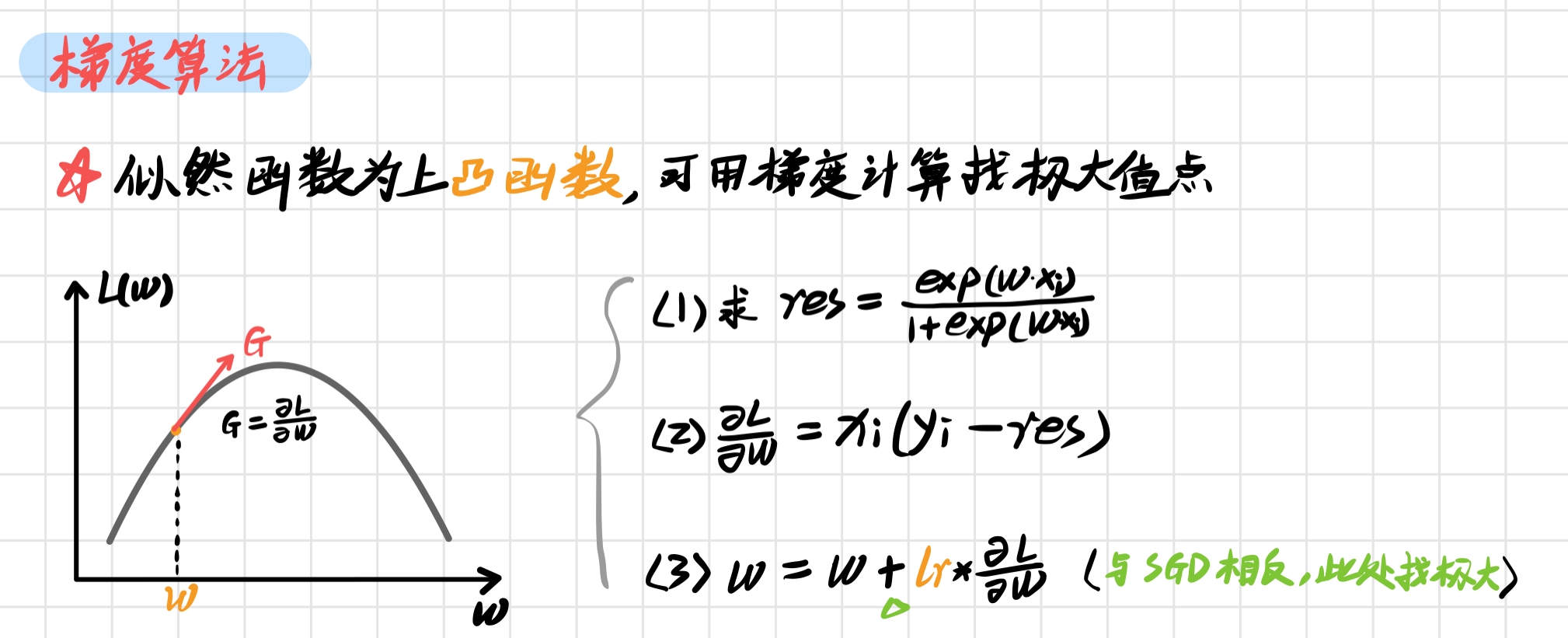
对应的代码为:
for x, y in zip(X, y) 可以得到索引一一对应的 x 和 y;
np.transpose 函数可以将矩阵转置,np.dot() 可以进行矩阵相乘运算;
def fit(self, X, y):
X = self.expand(X)
self.weights = np.zeros((len(X[0]), 1), dtype=np.float32) # columnn matrice
for iter_ in range(self.max_iter):
for item_x, item_y in zip(X, y):
res = self.sigmoid(np.dot(item_x, self.weights))
self.weights += self.learning_rate * (item_y - res) * np.transpose([item_x])
(4) 预测时,通过判断 sigmoid(wx) 是否满足大于0.5,小于 0.5 判为 0 类,或者判为 1 类
2.3 测试结果
我们测试一下模型的得分:
clf = LogisticRegressionClassifier()
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))
x_ponits = np.arange(4, 8)
y_ = -(clf.weights[0]*x_ponits + clf.weights[2])/clf.weights[1]
plt.plot(x_ponits, y_)
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()
plt.show()
预测得分 1.0 🍻
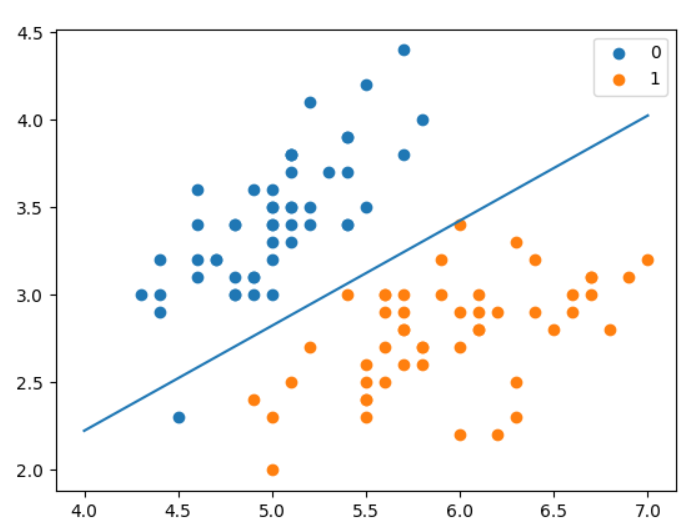
3. scikit-learn 实例
3.1 LogisticRegression
在 scikit-learn 的线性模型 Linear Model 中包含了模型 LogisticRegression,使用方法可以参考 sklearn.linear_model.LogisticRegression?:
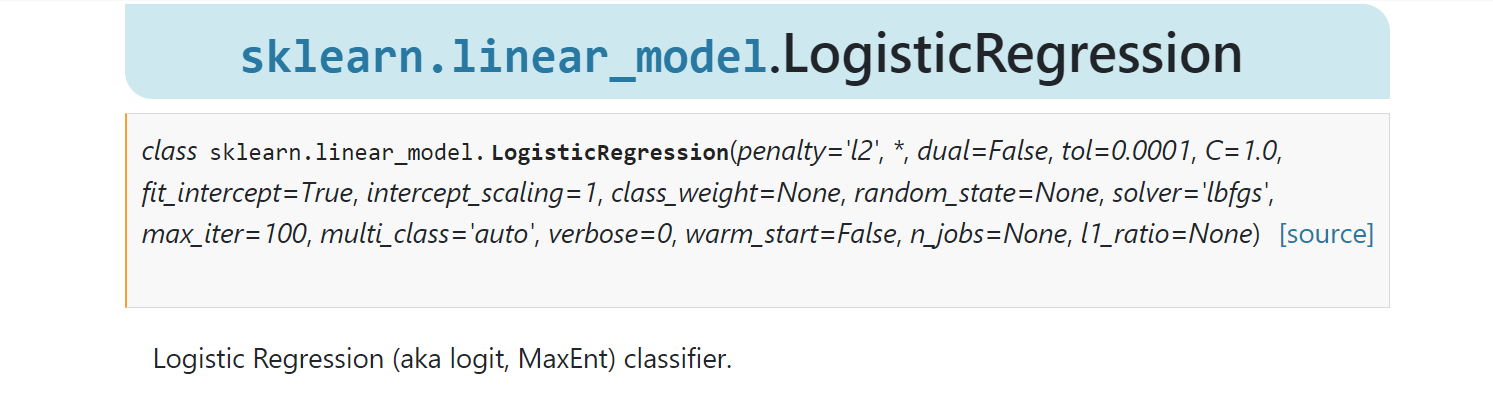
参数 solver
solver参数决定了我们对逻辑回归损失函数的优化方法,有四种算法可以选择,分别是:
- a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
- b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
- c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
- d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
3.2 Example
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
def create_data():
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sl', 'sw', 'pl', 'pw', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
return data[:, [0, 1]], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
clf = LogisticRegression(max_iter=200)
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))
print(clf.coef_, clf.intercept_)
结果如下
1.0
[[ 2.86401035 -2.76369768]] [-6.92179114]
最后一行前一项为 w,最后一个为 独立的部分 b
REFERENCE
- 李航统计学习方法
- 机器学习
- scikit-learn