为啥想写这篇文章呢。。因为之前提到的图神经网络应用篇鸽了一年多了,把自己的研究方向做一个总结,并向其他同样研究方向的朋友做一个报告,如有错误,敬请指出。而且,这个研究方向人太少了,万望能借此引起更多人的关注与兴趣。废话不多说了,以下开启此篇正文。
图相似度计算(Graph Similarity)是图领域一个重要应用,与图片相似度(Image Similarity)不是一回事。针对图片相似度,比较常用的有:汉明距离、欧式距离、马氏距离等。传统的图相似度定义方法,常用的有:GED和MCS。
GED:Graph Edit Distance, 图编辑距离,提出的年代有点久远了,以至于我见过不同文章的引用里面不相同的情况。主要是参考了NLP领域的编辑距离思想,即:把一句话,经过增删改等操作,变成另一句话的操作次数。同理,图编辑距离即把图a经过对节点和边的操作(增、删、改)变为另一个图b(表现在相似度计算中,图a和图b是一对待测图)的最小操作次数。
MCS:Maximum Common Subgraph, 最大公共子图。即:一减去两图最大公共子图的节点数与两图各自节点数乘积的比值。如下图所示:
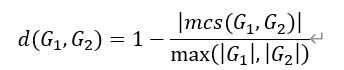
传统的定义法以及基于GED和MCS的改进方法(近似计算)被认为是NP-Hard问题,存在计算复杂度高的问题,所以研究人员提出了使用深度学习方法来解决图相似度计算难的问题。
Bai团队将深度学习方法应用到图相似度计算领域,且认为图结构数据包含两方面的特征,即:图级别特征和节点级别特征,提出了SimGNN。文章链接已给出,模型如图所示:
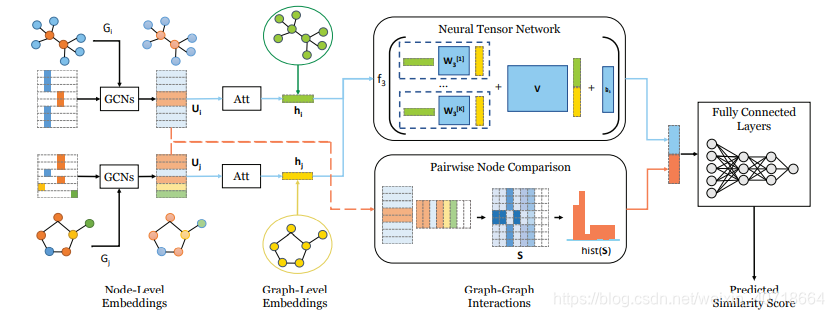
可以看到,SimGNN大体可以分为三个阶段:1)嵌入阶段(从节点嵌入到图嵌入) 2)交互阶段:图级特征、节点级特征捕获与融合 3)预测阶段:基于全连接神经网络的预测模块。
与传统的深度学习预测任务不同,图相似度标签不是人为标注(不依赖领域知识也没法依赖领域知识)。所以首先明确的一点是,标签是通过传统算法生成的,这一点引发了我的两个思考(个人认为第一点尤为重要):
1)标签是生成的,这意味着任何图结构数据,都可以两两一组,构建新的数据集,生成的数据集包含原始数据集的全部信息,并增加了图相似度作为新数据集的标签,这一点使得轻松构建私有数据集成为可能。
2)其次需要明确,深度学习方法本质上是为了训练完成后,相比于近似计算,可以准确且快速的完成大量成对图结构数据的相似度计算任务。
OK,回到正题。
SimGNN中,第一阶段是通过孪生图卷积神经网络(不了解什么是孪生神经网络的可以参考这里或这里)。给出一个某乎大佬贴的孪生神经网络(Siamese Network)的结构图吧:
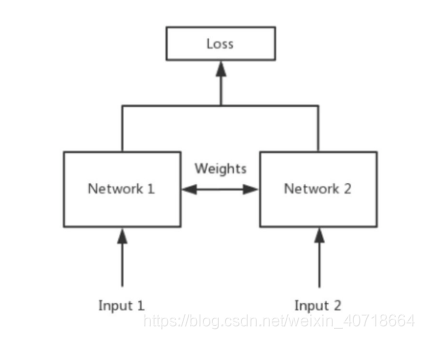
看过一个说法,孪生神经网络通过共享权值的方式,将成对的数据嵌入到同一个向量空间(特征空间),则可以通过计算向量距离(如:欧氏距离、余弦距离等)的方式,计算相似度(此处可以明确一个概念,相似度越大,向量在特征空间上的距离越小,相似度越小,距离越大)。而且,因为孪生神经网络共享权值的特性,只需实现单分支即可。
如上孪生神经网络结构图,最早用于验证(人脸验证、签名验证等),是度量学习的一种。SimGNN巧妙地把Siamese结构同GCN联系起来,用以生成图结构数据在特征空间的节点级嵌入。同时,SimGNN中用了一种Attention机制,将节点级嵌入转化为图级嵌入,式子如下:
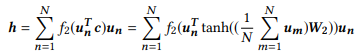
看到这里不要头疼,也没那么难懂(bushi)。从右往左看,式子中的un(最右边一项)为某个节点的节点嵌入(由上文提到的孪生图神经网络生成),W2是可学习的权重矩阵,整个tanh(x)部分(c部分)其实就是通过平均计算每一个节点嵌入得到全局“视野”(文中称为:context,即全局上下文),f2就是我们熟悉的sigmoid了。需要着重理解一下,文中提到,全局上下文包括了一个图的全局结构和特征信息,所以输出h为图结构的全局嵌入。
至此,第一阶段结束。
第二阶段,SimGNN分为了两个分支,一个分支负责图级嵌入的进一步提取,另一个分支负责挖掘节点级信息(作者认为,一些图对之间的相似性更多的体现在小规模的子结构中),进而将图相关特征划分为图级交互信息和节点级交互信息。文章中,前者为主,后者为辅(作者提出,因节点级特征计算开销较大,必要时可以仅用图级嵌入分支结合预测模块计算相似度得分,但在我的实际实验中发现,单一分支针对小数据集表现十分不稳定,性能波动较大,大规模数据集上表现稍稳定,但在多个数据集上任有较大起伏)。
进一步处理图级嵌入

作者在这一部分,引入了一个叫神经张量网络的东西,用以进一步处理图级嵌入。我去扒了扒神经张量网络(Neural Tensor Network, NTN)的原文,模型结构图如下:
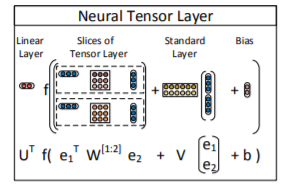
了解了一下,NTN是文本实体关系建模非常常用的一种方法(本人NLP战5渣,敬请批评指正),通过对嵌入向量的切片,构建双线性张量积(图中你看哪个部分最恶心,哪个部分就是双线性张量积),结合标准层,最后输出得分。
说了那么一大堆,还是看式子吧,定义式子如下:
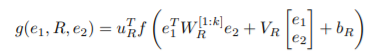
式子是不是简单明了呢?
当然不是!看到这里,duck不必直接吐血。
首先,等式左边为输出,是e1和e2的关系得分,右边,WR是张量切片,如模型图所示,W[1:2]表示两个切片,标准层为VR所在层(十分正常地捕捉e1和e2的关系),至于bR,就是我一直不知道有什么大用,但是想起来确实存在即合理的偏置项。如果等式右边第一项(UR的转置)去掉,这个式子将不输出e1和e2的得分,而是用来建模e1和e2之间的关系,SimGNN就是基于这一思路将NTN应用到处理图级嵌入中来的。如此,输出结果就是进一步处理后的图级交互特征,就等待着节点级交互来连接吧。
节点级嵌入
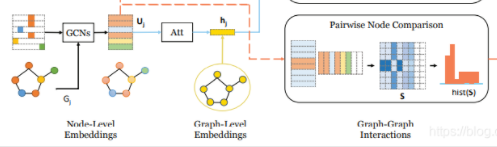
此处建议回到SimGNN模型图再看一次(好吧,我知道你们不会看,我再放一张):
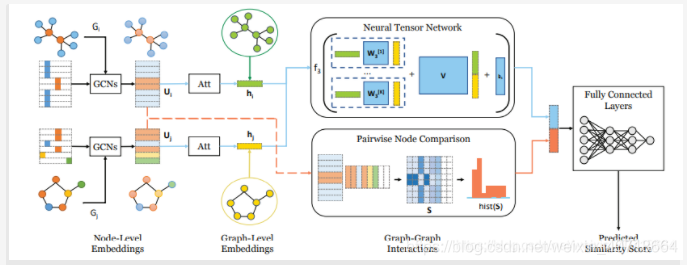
节点级交互特征矩阵,是在Att层之前拿到两个图各自的节点级嵌入通过相乘的方式获得,即:节点级特征直接构建节点特征交互矩阵。说白了,就是其中一个特征向量转置,二者相乘得到该交互矩阵。但向量相乘存在一个问题,维度不同无法相乘,表现在模型图中就是,第一个图结构数据(模型图左上角)有8个节点,生成8维嵌入特征向量,第二个图结构数据(模型图左下角)有6个节点,生成6维嵌入特征向量,二者无法相乘。文中设计了构造假节点(fake nodes)的方式,作了维度补齐(维度对齐),如图白色部分所示:
得到交互矩阵之后,作者文中提到,可以像正常处理图片一样,利用CNN做特征提取,但是我就不,我就任性地直接用直方图特征(实验中固定为16维)作为节点级信息补充。
文中指出,直方图特征不可训练,得到的向量是固定的。理论上(主观臆测)来说,于研究可能有益,但作用不会很大,为啥他敢这么做呢?我有两个大胆猜想:
1)直方图特征比想象中要牛,即:直方图特征信息丰富,且因不可训练,模型整体训练速度较快。
2)这一分支作用没这么大。
在实际对比实验中,我发现两个猜想都对,但都不够准确,简单总结:SimGNN的图级分支有用,但是对结果(MSE之类的指标)提升不大,主要作用体现在使得预测效果更加稳定,更像是图级分支(SimGNN策略一,即模型图中的上分支)作为攻坚克难的主力队员,但发挥不稳定,节点级特征单独表现不佳,但可以作为教练,时刻鞭策主力队员。SimGNN中,两个分支相对独立,不互为补充。
最后一个部分就是基于全连接神经网络的预测模块了,不讲,略过。
SimGNN的原版代码及Pytorch, Tensorflow代码复现在github上都有,大家自行搜索下载就好,需要注意的是数据预处理的方式。
简单总结:
- 文章比较重要的贡献:提供了深度学习方法计算图数据相似性的重要思路。
- 明确了节点级特征与图级特征之间的关系:节点级特征为图级特征的补充。
差不多到这里就写完了,我自己也是基于这个模型设计了一些新的方法,取得了不错的结果,不过截止此篇博客发出时间,文章还没投出,就不在这里展开啦。
如果对这个方向感兴趣,可以留言,或者私聊我,有时间可以进一步沟通。