[人工智能]使用tensorflow实现鸢尾花的分类

最近在学习深度学习，记录一下实现的过程

对北京大学曹健老师class1课程的总结

1、数据集的准备

数据集可以通过sklearn.datasets.load_iris直接获取

from sklearn.datasets import load_iris
iris_data = load_iris()
# 特征值
x_data = iris_data.data
# 目标值
y_data = iris_data.target

也可前往UCI机器学习库自己下载

2、数据集打乱，分割训练集和测试集

np.random.seed(116)
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 数据集分割，将数据集分为测试集和训练集 即 x_train,y_train,y_train,y_test
# 一般是将百分之80的数据作为训练集，剩下的百分之20位测试集
split_num = int(len(y_data) * 0.8)
x_train = x_data[:split_num]
y_train = y_data[:split_num]

# 测试集
x_test = x_data[split_num:]
y_test = y_data[split_num:]

# 将特征值的类型转换为tensor类型，避免后面的矩阵乘法报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

?将特征值和目标值一一配对起来

train_data = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_data = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

在神经网络中，数据是以batch为单位喂入网络的，这里将32组数据分为一个batch

使用梯度下降优化模型

梯度下降公式

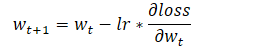
其中?lr?是超参数，指学习率，学习率的设置不能过大也不能过小

如果学习率过小，模型容易陷入局部最优解，且收敛缓慢，学习率过大，梯度可能会在最小值附近来回震荡，甚至可能无法收敛，所以，学习率的设置在深度学习中尤为关键，对于学习率的调整可以参考这篇博文学习率(Learning rate)的理解以及如何调整学习率

初始化梯度、偏置、学习率、下降次数、每一轮的总损失

这里由于数据集的缘故不对学习率做调整，给出一个0.1即可

# 初始化梯度和偏置
# 由于输入的特征为4个，目标值是三分类，所以我们将 梯度 随机初始化为 四行三列的tensor
w = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1))
# 同理，我们的目标值是一维数据，所以将 偏置 初始化为随机的1维tensor
b = tf.Variable(tf.random.truncated_normal([3], stddev=0.1))

# 初始化学习率
lr = 0.1
# 梯度下降次数
epoch = 500
# 每轮分4个step，loss_all记录四个step生成的4个loss的和
loss_all = 0

3、训练部分

for epoch in range(epoch):
    for step, (x_train, y_train) in enumerate(train_data):
        with tf.GradientTape() as tape:
            y = tf.matmul(x_train, w) + b
            # 使输出符合概率分布
            y = tf.nn.softmax(y)
            # 将目标值转换为独热编码，方便计算loss和acc
            y_true = tf.one_hot(y_train, depth=3)
            # 回归性能评估采用MSE
            loss = tf.reduce_mean(tf.square(y_true - y))
            # print(loss)
            loss_all += loss.numpy()
        # 对每个梯度和偏置求偏导
        grads = tape.gradient(loss, [w, b])
        # 梯度自更新
        # 这两行代码相当于
        # w = w - lr * w_grads、b = b - lr * b_grads
        w.assign_sub(lr * grads[0])
        b.assign_sub(lr * grads[1])
    print(f"第{epoch}轮,损失是:{loss_all / 4}")
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

?原理为：

? ? ? ? 将输入的四个特征与初始化的权重w做矩阵乘法再与偏置b求和(线性回归)，会得到三个结果，即属于各个分类的概率，由于第一次的w和b都是随机给出的，所以第一次的估计神经网络完全就是瞎蒙的，之后不断地对w和b求偏导做优化，使其不停的逼近真实值，进而提高模型的准确率，tensorflow里，指定参数对函数求偏导可以用 tf.GradientTape.gradient?这个api

该案例采用的评估公式为MSE

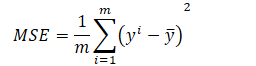
?代码的表示为

loss = tf.reduce_mean(tf.square(y_true - y))

?将结果传入softmax是为了使其符合概率分布(总和为1)

下面是softmax的具体计算公式

?y代表输入哪个分类的概率

?下面是全部代码

# -*- coding:utf-8 -*-
import numpy as np
from sklearn.datasets import load_iris
import tensorflow as tf

# 从 sklearn中加载鸢尾花数据集
iris_data = load_iris()
# 特征值
x_data = iris_data.data
# 目标值
y_data = iris_data.target

# print(len(x_data),y_data)
# 打乱数据集
# 设置随机数种子,确保打乱后的数据仍然是一组组对应的数据
np.random.seed(116)
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 数据集分割，将数据集分为测试集和训练集 即 x_train,y_train,y_train,y_test
# 一般是将百分之80的数据作为训练集，剩下的百分之20位测试集
split_num = int(len(y_data) * 0.8)
x_train = x_data[:split_num]
y_train = y_data[:split_num]

# 测试集
x_test = x_data[split_num:]
y_test = y_data[split_num:]

# 将特征值的类型转换为tensor类型，避免后面的矩阵乘法报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# 将特征值和目标值一一配对 并且每32组数据为一个batch，喂入神经网络的数据以batch为单位
train_data = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_data = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# print(test_data)

# 初始化梯度和偏置
# 由于输入的特征为4个，目标值是三分类，所以我们将 梯度 随机初始化为 四行三列的tensor
w = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1))
# 同理，我们的目标值是一维数据，所以将 偏置 初始化为随机的1维tensor
b = tf.Variable(tf.random.truncated_normal([3], stddev=0.1))

# 初始化学习率
lr = 0.1
# 梯度下降次数
epoch = 500
# 每轮分4个step，loss_all记录四个step生成的4个loss的和
loss_all = 0
for epoch in range(epoch):
    for step, (x_train, y_train) in enumerate(train_data):
        with tf.GradientTape() as tape:
            y = tf.matmul(x_train, w) + b
            # 使输出符合概率分布
            y = tf.nn.softmax(y)
            # 将目标值转换为独热编码，方便计算loss和acc
            y_true = tf.one_hot(y_train, depth=3)
            # 回归性能评估采用MSE
            loss = tf.reduce_mean(tf.square(y_true - y))
            # print(loss)
            loss_all += loss.numpy()
        # 对每个梯度和偏置求偏导
        grads = tape.gradient(loss, [w, b])
        # 梯度自更新
        # 这两行代码相当于
        # w = w - lr * w_grads、b = b - lr * b_grads
        w.assign_sub(lr * grads[0])
        b.assign_sub(lr * grads[1])
    print(f"第{epoch}轮,损失是:{loss_all / 4}")
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_data:
        y = tf.matmul(x_test, w) + b
        y = tf.nn.softmax(y)
        # 返回最大值所在的索引，即预测的分类
        y_pred = tf.argmax(y, axis=1)
        # print(y_pred)
        y_pred = tf.cast(y_pred, dtype=y_test.dtype)
        # 预测正确为1，错误为0
        correct = tf.cast(tf.equal(y_pred, y_test), dtype=tf.int32)
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    acc = total_correct / total_number
    print("测试集的准确率为:\n", acc)
    print("---------------------------------")

?截取一段运行结果

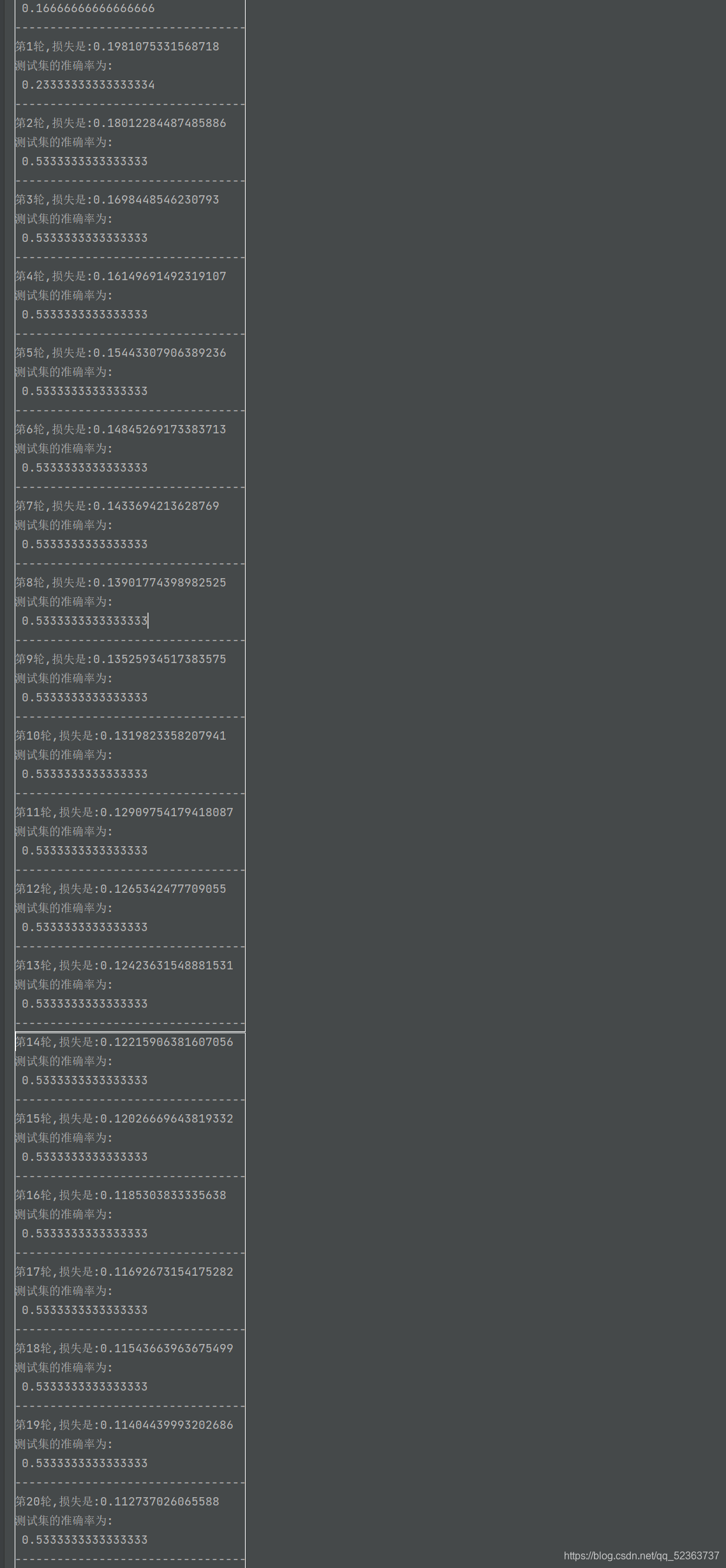
?可见在前面的训练中，loss的减少是非常可观的，它在快速的逼近这个真实值

更新了170次左右，这个w跟b就已经非常逼近真实值了，但继续迭代，loss仍然会得到优化

?
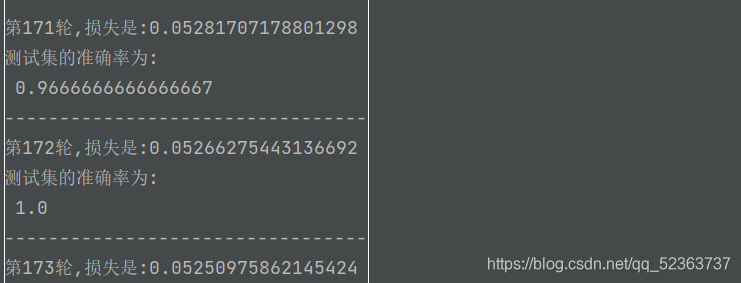