K近邻
一个例子弄懂k-近邻
电影可以按照题材分类,每个题材又是如何定义的呢?那么假如两种类型的电影,动作片和爱情片。动作片有哪些公共的特征?那么爱情片又存在哪些明显的差别呢?我们发现动作片中打斗镜头的次数较多,而爱情片中接吻镜头相对更多。当然动作片中也有一些接吻镜头,爱情片中也会有一些打斗镜头。所以不能单纯通过是否存在打斗镜头或者接吻镜头来判断影片的类别。那么现在我们有6部影片已经明确了类别,也有打斗镜头和接吻镜头的次数,还有一部电影类型未知。
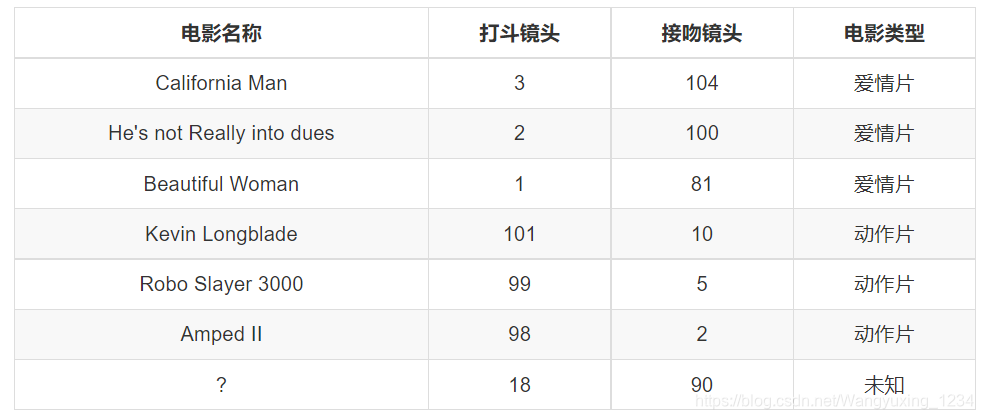
那么我们使用K-近邻算法来分类爱情片和动作片:存在一个样本数据集合,也叫训练样本集,样本个数M个,知道每一个数据特征与类别对应关系,然后存在未知类型数据集合1个,那么我们要选择一个测试样本数据中与训练样本中M个的距离,排序过后选出最近的K个,这个取值一般不大于20个。选择K个最相近数据中次数最多的分类。那么我们根据这个原则去判断未知电影的分类
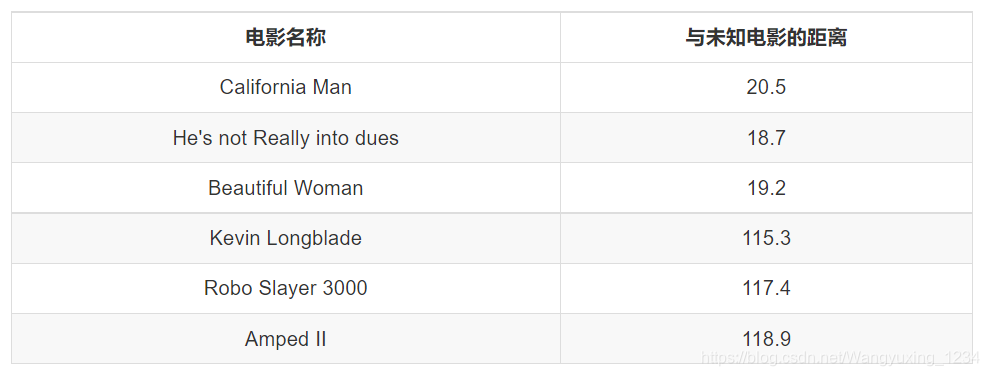
我们假设K为3,那么排名前三个电影的类型都是爱情片,所以我们判定这个未知电影也是一个爱情片。那么计算距离是怎样计算的呢?
欧氏距离 如果说输入变量有四个特征,例如(1,3,5,2)和(7,6,9,4)之间的距离计算为: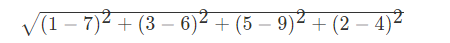
sklearn k-近邻算法API
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)
- n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法:‘ball_tree’将会使用BallTree,‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)
实例代码如下:
def knncls():
"""
K-近邻预测用户签到位置
:return:
"""
data = pd.read_csv("D:/钉钉下载/facebook-v-predicting-check-ins/train.csv/train.csv")
# print(data.head(10))
data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")
time_value = pd.to_datetime(data['time'], unit='s')
# print(time_value)
time_value = pd.DatetimeIndex(time_value)
# print(time_value)
data['day'] = time_value.day
data['hour'] = time_value.hour
data['weekday'] = time_value.weekday
data = data.drop(['time'], axis=1)
# print(data)
place_count = data.groupby('place_id').count()
# print(place_count)
tf = place_count[place_count.row_id > 3].reset_index()
data = data[data['place_id'].isin(tf.place_id)]
y = data['place_id']
x = data.drop(['place_id'], axis=1)
x_train, x_test, y_train, y_test =train_test_split(x, y, test_size=0.25)
std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
knn = KNeighborsClassifier()
knn.fit(x_train, y_train)
y_predict = knn.predict(x_test)
print("预测的目标签到位置为:", y_predict)
print("预测的准确率:", knn.score(x_test, y_test))
k-近邻算法优缺点:
优点:
简单,易于理解,易于实现,无需估计参数,无需训练
缺点:
懒惰算法,对测试样本分类时的计算量大,内存开销大必须指定K值,K值选择不当则分类精度不能保证
使用场景:小数据场景,几千~几万样本,具体场景具体业务去测试
朴素贝叶斯
朴素贝叶斯(Naive Bayes)是一个非常简单,但是实用性很强的分类模型。朴素贝叶斯分类器的构造基础是贝叶斯理论。
概率论基础
概率定义为一件事情发生的可能性。事情发生的概率可以 通过观测数据中的事件发生次数来计算,事件发生的概率等于改事件发生次数除以所有事件发生的总次数。举一些例子:
- 扔出一个硬币,结果头像朝上
- 某天是晴天
- 某个单词在未知文档中出现
联合概率:包含多个条件,且所有条件同时成立的概率
记作:𝑃(𝐴,𝐵)
条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率
记作:𝑃(𝐴|𝐵)
特性:P(A1,A2|B) = P(A1|B)P(A2|B)
注意:此条件概率的成立,是由于A1,A2相互独立的结果
贝叶斯公式
𝑃(𝐶│𝑊)=(𝑃(𝑊│𝐶)𝑃(𝐶))/(𝑃(𝑊))
注:w为给定文档的特征值(频数统计,预测文档提供),c为文档类别
公式可以理解为:
𝑃(𝐶│𝐹1,𝐹2,…)=(𝑃(𝐹1,𝐹2,… │𝐶)𝑃(𝐶))/(𝑃(𝐹1,𝐹2,…))
其中c可以是不同类别
公式分为三个部分:
𝑃(𝐶):每个文档类别的概率(某文档类别词数/总文档词数)
𝑃(𝑊│𝐶):给定类别下特征(被预测文档中出现的词)的概率
计算方法:𝑃(𝐹1│𝐶)=𝑁𝑖/𝑁 (训练文档中去计算)
𝑁𝑖为该𝐹1词在C类别所有文档中出现的次数
N为所属类别C下的文档所有词出现的次数和
𝑃(𝐹1,𝐹2,…) 预测文档中每个词的概率
拉普拉斯平滑
𝑃(𝐹1│𝐶)=(𝑁𝑖+𝛼)/(𝑁+𝛼𝑚)
𝛼为指定的系数一般为1,m为训练文档中统计出的特征词个数
sklearn朴素贝叶斯实现API
sklearn.naive_bayes.MultinomialNB
sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
朴素贝叶斯算法案例:
- sklearn20类新闻分类
- 20个新闻组数据集包含20个主题的18000个新闻组帖子
实例代码如下:
def naviebayes():
"""
朴素贝叶斯
:return:
"""
news = fetch_20newsgroups(subset='all')
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
tf = TfidfVectorizer()
x_train = tf.fit_transform(x_train)
print(tf.get_feature_names())
x_test = tf.transform(x_test)
mlt = MultinomialNB(alpha=1.0)
print(x_train.toarray())
mlt.fit(x_train, y_train)
y_predict = mlt.predict(x_test)
print("预测的文章类别为:", y_predict)
print("准确率为:", mlt.score(x_test, y_test))
朴素贝叶斯分类优缺点:
优点:
朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
对缺失数据不太敏感,算法也比较简单,常用于文本分类。
分类准确度高,速度快。
缺点:
需要知道先验概率P(F1,F2,…|C),因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。