摘要

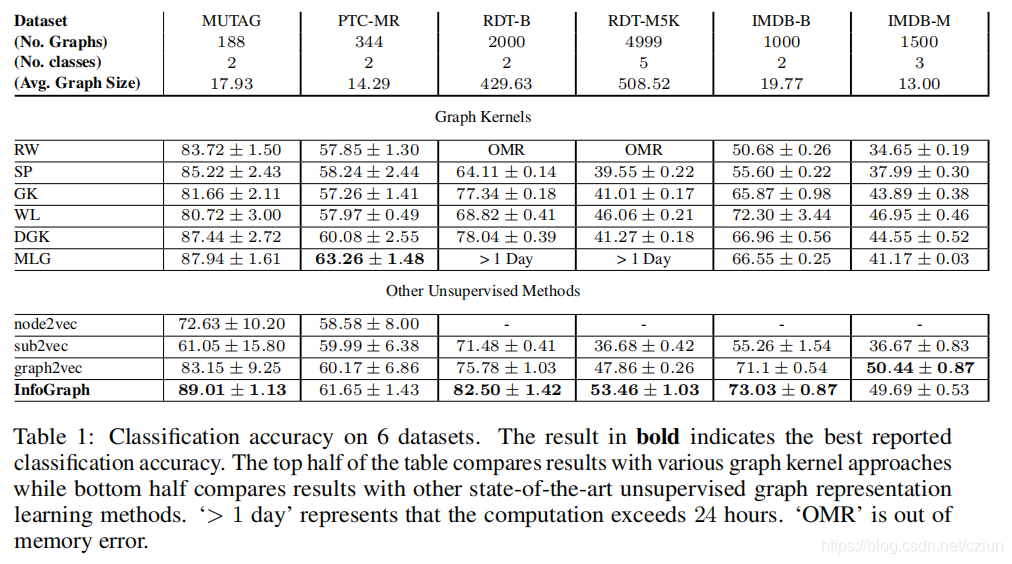
本文研究了在无监督和半监督场景下学习整个图的表示。图级表示在各种现实应用中至关重要，如预测分子的性质和社交网络中的社区分析。传统的基于图核的方法虽然简单，对于获得图的固定长度的表示很有效，但由于手工设计，它们的泛化性较差。最近也有一些基于语言模型（例如，graph2vec）的方法，但它们都倾向于只考虑某些子结构（例如，子树）作为图的代表。

受无监督表示学习最新进展的启发，本文提出了一种新的学习图级表示的方法——InfoGraph。我们最大化图级表示和不同尺度（如节点、边、三角形）的子结构表示之间的互信息。通过这样做，图级表示可以对在不同规模的子结构中共享的数据的各个方面进行编码。此外，我们进一步提出了InfoGraph*，这是半监督场景的扩展。InfoGraph* 最大化InfoGraph学到的无监督图表示与现有监督方法学到的表示之间的互信息。因此，监督编码器从未标记的数据中学习，同时保留当前监督任务所偏好的潜在语义空间。对图分类和分子性质预测的实验结果表明，InfoGraph优于最先进的基线，InfoGraph*可以实现与最先进的半监督模型的性能竞争。

1 方法

最近有关图的工作集中在监督学习任务或学习节点表示。然而，许多图的分析任务，如图的分类、回归和聚类，都需要将整个图表示为固定长度的特征向量。虽然图级表示可以通过节点级表示隐式获得，但显式地提取图对于面向图的任务可以更直接和更优。

在本节中，我们首先制定一个无监督的整个图的表示学习问题和一个图上的半监督预测任务。然后，我们提出了我们的学习图级表示的方法。然后，我们提出了我们提出的半监督学习场景的模型。
在这里插入图片描述

1.1 问题定义

（1）无监督的图表示学习

给定一组图 $\mathbb{G}=\{G_1,G_2,…\}$ 和一个正整数 $δ$ （预期的嵌入大小），我们的目标是学习每个图 $G_i∈\mathbb{G}$ 的 $δ$ 维分布表示。我们将 $G_i$ 中的节点数表示为 $G_i|$ 。我们将所有图的表示的矩阵表示为 $Φ∈\mathbb{R}^{|\mathbb{G}|×δ}$ 。

（2）半监督的图预测任务

给定一组标记的图 $\mathbb{G}^L=\{G_1,· · ·,G_{|\mathbb{G}^L|}\}$ 和相应的输出 $\{o_1,···,o_{|\mathbb{G}^L|}\}$ 以及一组未标记的样本 $\mathbb{G}^U=\{G_{|\mathbb{G}^L|+1},· · ·,G_{|\mathbb{G}^L|+|\mathbb{G}^U|}\}$ ，我们的目标是学习一个模型，可以对看不见的图做出预测。在大多数情况下， $|\mathbb{G}^U|>>|\mathbb{G}^L|$ 。

1.2 InfoGraph

我们关注的是图神经网络(GNNs)——一类灵活的嵌入架构，它通过在局部节点邻域上的重复聚合来生成节点表示。节点的表示是通过聚合其邻域节点的特征来学习的，因此我们将这些表示称为补丁表示。GNN利用一个读出函数将所有获得的补丁表示总结为一个固定长度的图级表示。

形式上，GNN的第 $k$ 层是：
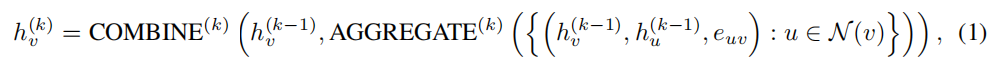
在这里插入图片描述
其中， $h^{(k)}_v$ 是节点 $v$ 在第 $k$ 个迭代/层处的特征向量（或以节点 $i$ 为中心的补丁表示）。读出函数可以是一个简单的排列不变函数，如平均，或一个更复杂的图级池化函数。

我们试图通过最大化图级和补丁级表示之间的互信息来获得图表示。通过这样做，图表示可以学习****对跨所有子结构共享的数据进行编码。假设我们得到一组训练样本 $\pmb{G}:=\{G_j∈ \mathbb{G}\}^N_{j=1}$ ，输入空间上的经验概率分布为 $\mathbb{P}$ 。设 $\phi$ 表示 $K$ 层GNN的参数集。在GNN的前 $k$ 层后，输入图将被编码成一组补丁表示 $\{h^{(k)}_i\}^N_{i=1}$ 。接下来，我们将GNN所有深度的特征向量总结为一个特征向量，该特征向量在以每个节点为中心的不同尺度上捕获补丁信息。我们使用连接。即：
在这里插入图片描述
其中， $h^i_\phi$ 是以节点 $i$ 为中心的总结补丁表示， $H_\phi(G)$ 是应用读出函数后的全局表示。

我们定义了全局/局部对上的互信息(MI)估计器，在给定的数据集 $\pmb{G}:=\{G_j∈ \mathbb{G}\}^N_{j=1}$ 上最大化了MI：
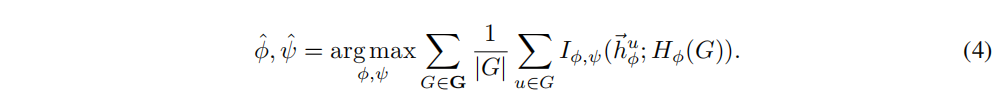
在这里插入图片描述
$I_{\phi,ψ}$ 是由discriminator $T_ψ$ 建模的互信息估计器，由参数为 $ψ$ 的神经网络参数化。我们使用Jensen-Shannon互信息估计器：

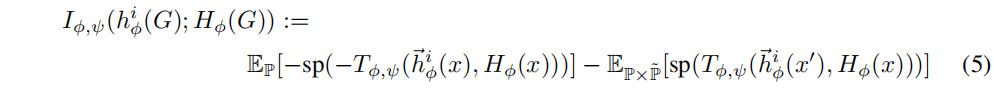
其中， $x$ 是一个输入样本， $x^{'}$ （负样本）是从 $\widetilde{\mathbb{P}}=\mathbb{P}$ 采样的输入（与输入空间的经验概率分布相同的分布）， $sp(z)=log(1+e^z)$ 为softplus函数。在实践中，我们使用一个batch中的所有图中全局和局部补丁表示的所有可能组合来生成负样本。

由于 $H_\phi(G)$ 被鼓励对包含所有尺度信息的补丁有高的MI，这有利于编码跨补丁共享的数据和跨尺度共享的数据。该算法如图1所示。

该模型与DGI的不同：

DGI使用随机抽样来获取负样本，因为它们主要集中于学习图上的节点嵌入。然而，对比方法需要大量的负例，因此，使用分批生成的负样本是至关重要的，我们正试图学习给定许多图形实例的图嵌入。
我们使用GIN作为图卷积编码器，而DGI使用GCN，因为GIN为图级应用程序提供了更好的inductive偏差。应仔细考虑图神经网络的设计，以便图表示可以区别于其他图实例。例如，我们使用求和来读出，这可以提供关于图的大小的重要信息。

2.3 半监督InfoGraph

基于之前的无监督模型，对图进行半监督性质预测的一种简单方法是将监督损失与作为正则化项的无监督目标函数相结合。在此过程中，该模型被训练来预测标记数据集的属性，同时保持从标记数据集和未标记数据集学习到的丰富的区别性中间表示。也就是说，我们尽量最小化以下目标函数：
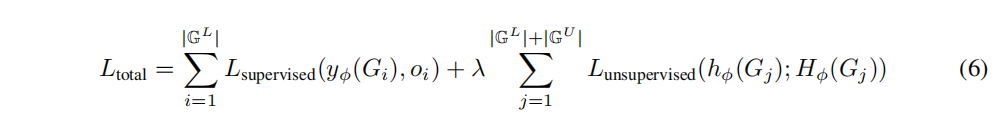
在这里插入图片描述
$\lambda$ 为超参数，控制了监督损失和无监督损失之间的相对权重。该模型将受益于从大量的未标签数据中学习良好的表示，同时学习预测相应的监督标签。

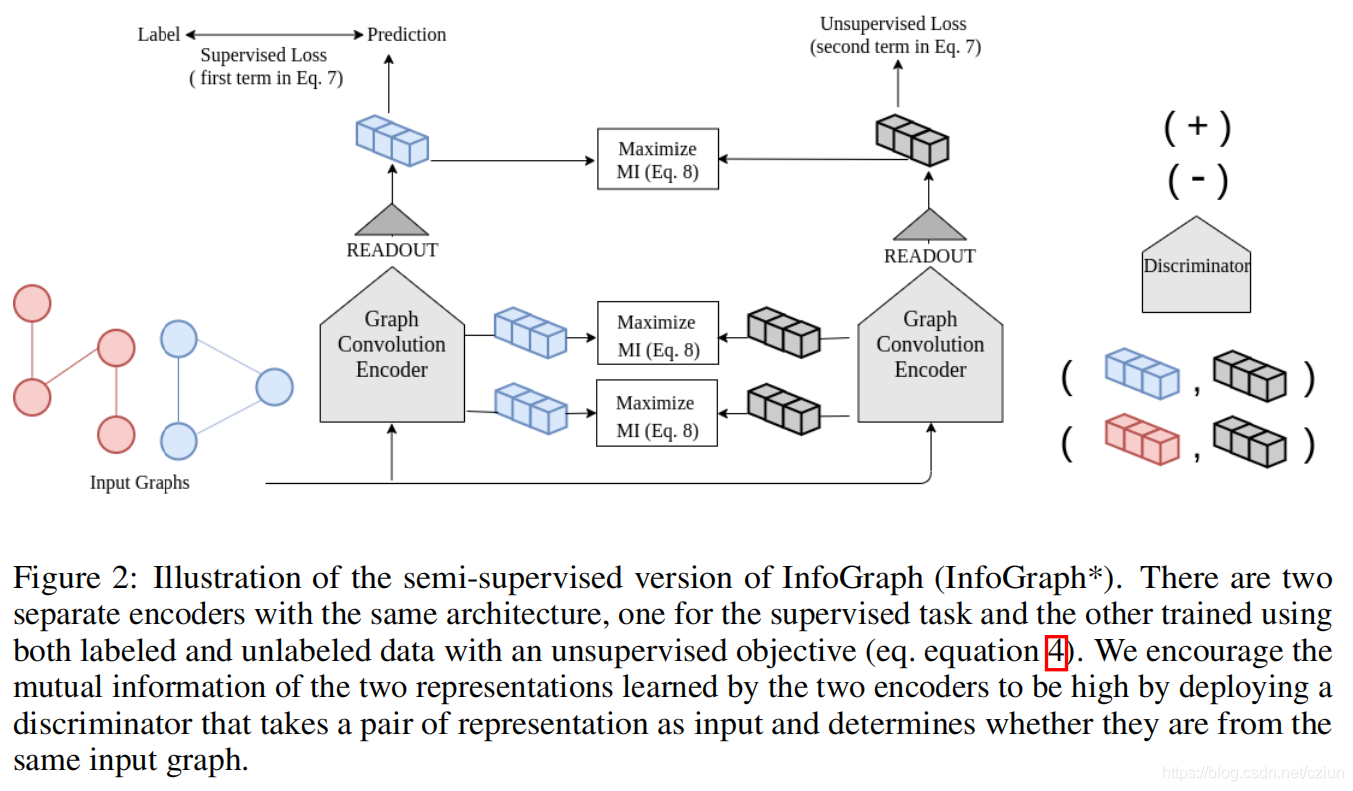
然而，监督任务和无监督任务可能有利于不同的信息或不同的语义空间。使用相同的编码器简单地合并这两个损失函数可能会导致“负转移”。我们提出了一种简单的方法来缓解这个问题：我们部署了两个编码器模型：标记数据上的编码器（有监督的编码器）和未标记数据上的编码器（无监督的编码）。为了将学习到的表示从无监督编码器转移到监督编码器，我们定义了一个损失项，鼓励两个编码器学习到的表示在所有表示层次上都具有较高的互信息（公式(8)的第三项）。形式上，让 $φ$ 表示另一个 $k$ 层图神经网络的参数集，另一个通过 $\phi$ 参数化，并让 $\lambda$ 是一个可调的超参数， $H^k_\phi(G)$ ， $H^k_φ(G)$ 是图 $G$ 在编码器层 $k$ 处的全局表示，总损失函数定义如下：
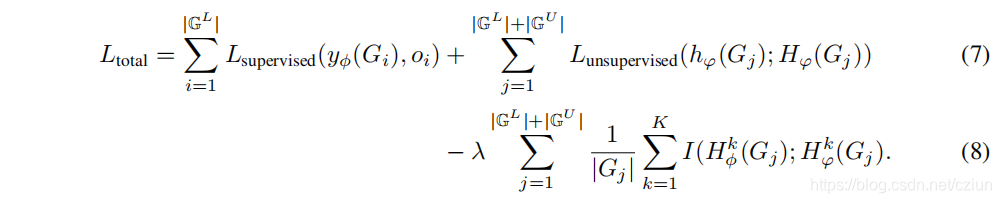
在这里插入图片描述
实际上，为了减少公式(8)的第三项引入的计算开销，在每次训练更新时，我们在编码器的随机选择层上强制执行互信息最大化，而不是在编码器的所有层上强制执行互信息最大化。