一、前言
机器学习的监督学习算法主要分为回归和分类问题,本文章介绍的是回归问题。
我们学习的第一个算法是线性回归算法,而线性回归算法中最常用的是梯度下降算法。在了解梯度算法之前应当先了解假设函数、代价函数的概念,继而加深对线性回归的梯度下降算法的了解,文章最后介绍了正规方程,以及与梯度下降算法的区别与应用场景。
注: 文章整理基于吴恩达机器学习视频
二、模型描述
还是从“预测房价”的例子入手,我们要使用的一个数据集,数
据集包含俄勒冈州波特兰市的住房价格。
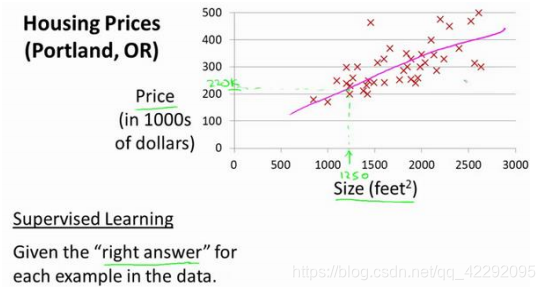
常见术语概念
在监督学习中我们有一个数据集,这个数据集被称训练集。
𝑚 代表训练集中实例的数量
𝑥 代表特征/输入变量
𝑦 代表目标变量/输出变量
(𝑥, 𝑦) 代表训练集中的实例
(𝑥(𝑖), 𝑦(𝑖)) 代表第𝑖 个观察实例
? 代表学习算法的解决方案或函数也称为假设(hypothesis)
? 是一个从𝑥 到 𝑦 的函数映射
监督学习过程:

Training set :训练集
选择最初的使用规则?代表 hypothesis,因而,要解决房价预测问题,我们实际上是要将训练集“喂”给我们的学习算法,进而学习得到一个假设?,然后将我们要预测的房屋的尺寸作为输入变量输入给?,预测出该房屋的交易价格作为输出变量输出为结果。
一种可能的表达方式为:?𝜃(𝑥) = 𝜃0 + 𝜃1𝑥,因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题。
注:这里的单变量线性回归问题可以与六多元梯度下降算法做对比来学习
?𝜃(𝑥)即为假设函数,当我们设计一个学习算法时,下一步需要决定怎么表达这个h,h的作用为预测一个y关于x的线性函数。
三、代价函数
我们可以根据假设函数画出代价函数,即代价函数是来实现以上模型的。

代价函数也被称作平方误差函数,有时也被称为平方误差代价函数。平方误差代价函数是解决回归问题最常用的手段了.
代价函数表达式: 𝐽(𝜃0, 𝜃1) = 1/2𝑚 ∑ (?𝜃(𝑥(𝑖)) ? 𝑦(𝑖))^2
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数取得最小。
Eg1:
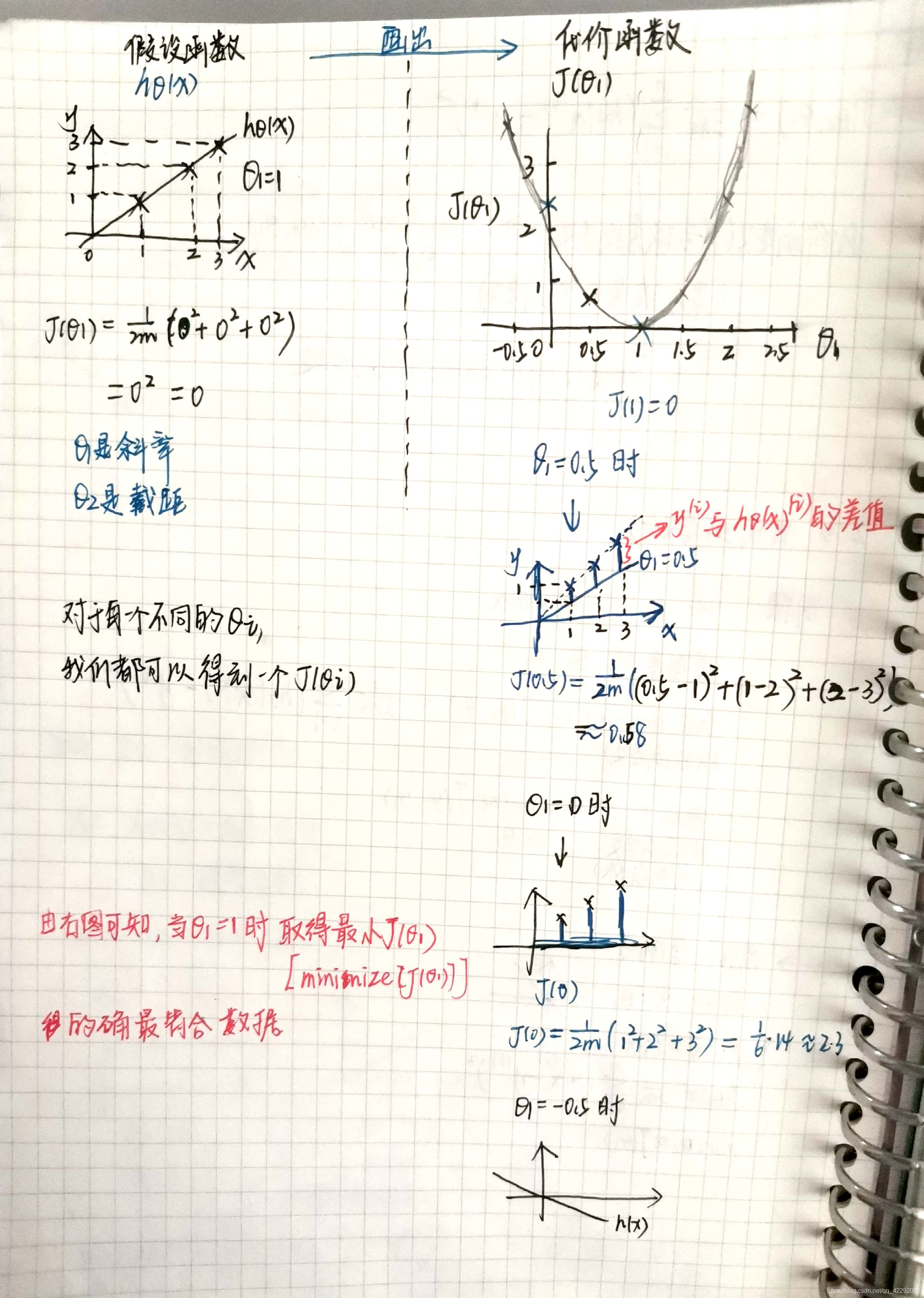
为了更直观的理解,我们以保留参数𝜃1为例,如下图中,对每一个假设函数都可以相应的画出代价函数中的坐标,进而求得代价函数中的最低点(即我们需要的最小值)。
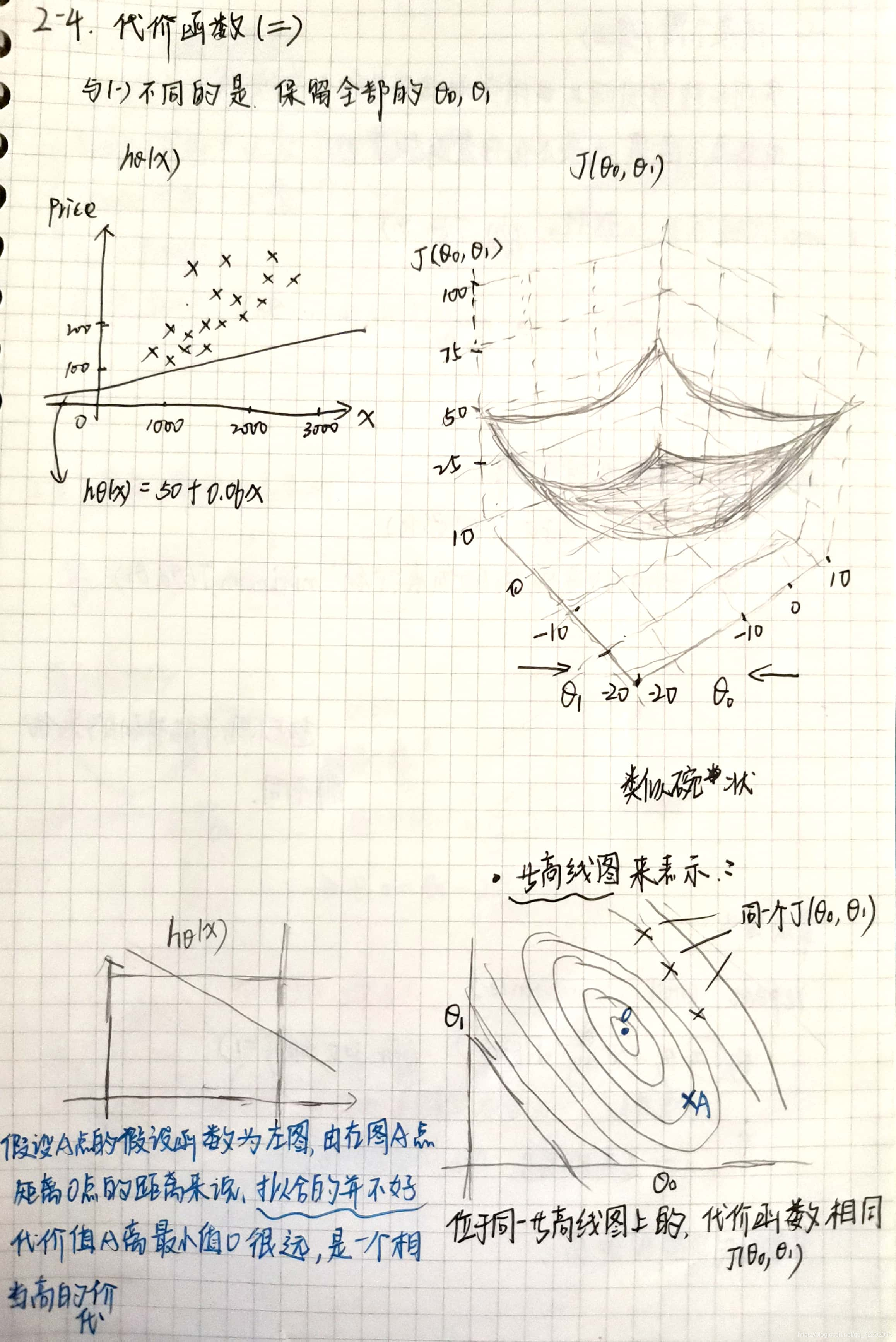
Eg2:保留全部的参数𝜃0, 𝜃1
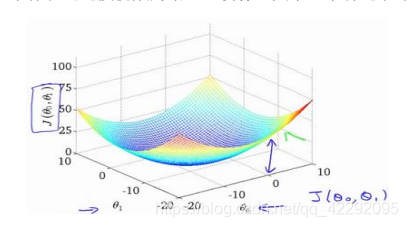
保留了全部参数的代价函数的样子类似于碗状,则可以看出在三维空间中存在一个使得𝐽(𝜃0, 𝜃1)最小的点。
我们常常看等高线,位于同一等高线图上的,代价函数相同。
当然,我们真正需要的是一种有效的算法,能够自动地找出这些使代价函数𝐽取最小值的参数𝜃0和𝜃1来。
在下面,我们将介绍一种算法-梯度下降算法,能够自动地找出能使代价函数𝐽最小化的参数𝜃0和𝜃1的值。
四、梯度下降算法
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数𝐽(𝜃0, 𝜃1) 的最小值。
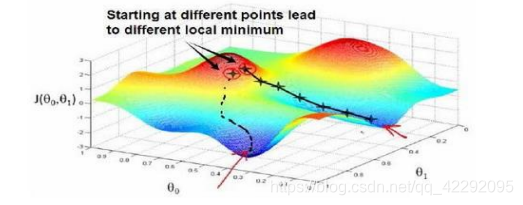
梯度下降背后的思想是:开始时我们随机选择一个参数的组合(𝜃0, 𝜃1, . . . . . . , 𝜃𝑛),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。**即起点不同,可能得到的最优解不同。**即一般的梯度下降算法是可以得到多个局部最优解的,与下面要介绍的线性回归的梯度下降算法不同,线性回归的梯度下降算法没有局部最优解的概念,只有全局最优解。

其中𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
在梯度下降算法中,梯度下降中,我们要同时更新𝜃0和𝜃1。
那研究𝑎是为了干什么呢?
- 𝑎太大时:向下迈出的步伐太大,有可能导致越过最低点,导致无法收敛甚至发散。
- 𝑎太小时:向下迈出的步伐太小,需要很多步去到达最低点,下降的太慢。
假设你将𝜃1初始化在局部最低点,下一步的梯度下降会怎么样?
假设你将𝜃1初始化在局部最低点,在这儿,它已经在一个局部的最优处或局部最低点------>局部最优点的导数将等于零------->它使得𝜃1不再改变,也就是新的𝜃1等于原来的𝜃1----->那么梯度下降法更新其实什么都没做,它不会改变参数的值。
这也解释了为什么即使学习速率𝑎保持不变时,梯度下降也可以收敛到局部最低点。
五、线性回归的梯度下降算法
将梯度下降和代价函数结合=线性回归算法(可以用直线模型来拟合数据)
将代价函数代入到梯度下降算法公式中


”批量梯度下降”,指的是在梯度下降的每一步中,我们都用到了
所有的训练样本,在梯度下降中,在计算微分求导项时,我们需要进行求和运算,所以,在每一个单独的梯度下降中,我们最终都要计算这样一个东西,这个项需要对所有𝑚个训练样本求和。
目前。我们已经掌握了批量梯度算法,并且能把它应用到线性回归中了,这就是用于线性回归的梯度下降法。
下一篇我们将介绍“多变量线性回归问题”