EM聚类也被叫成最大期望算法
具体的实现步骤主要为三步:
- 初始化参数
- 观察预期
- 重新估计
EM算法的工作原理
假设一个例子
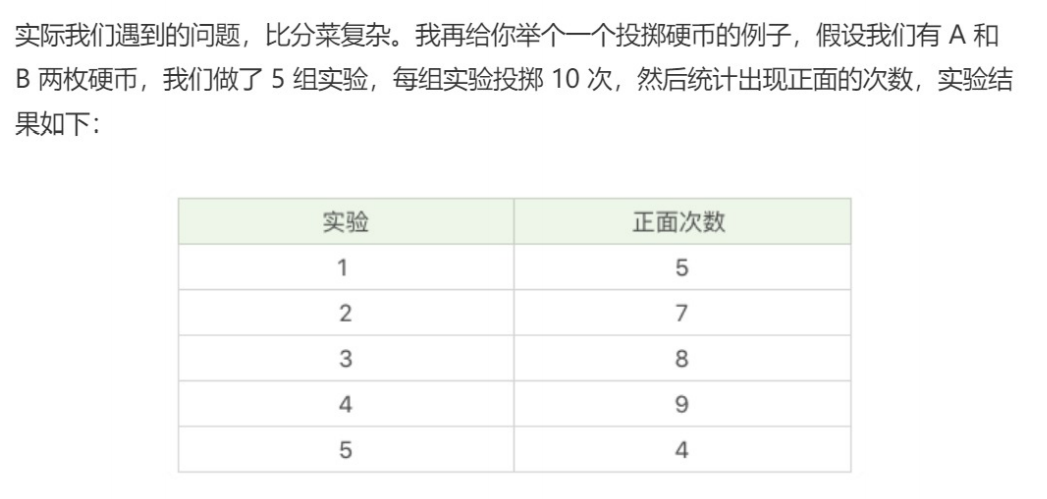
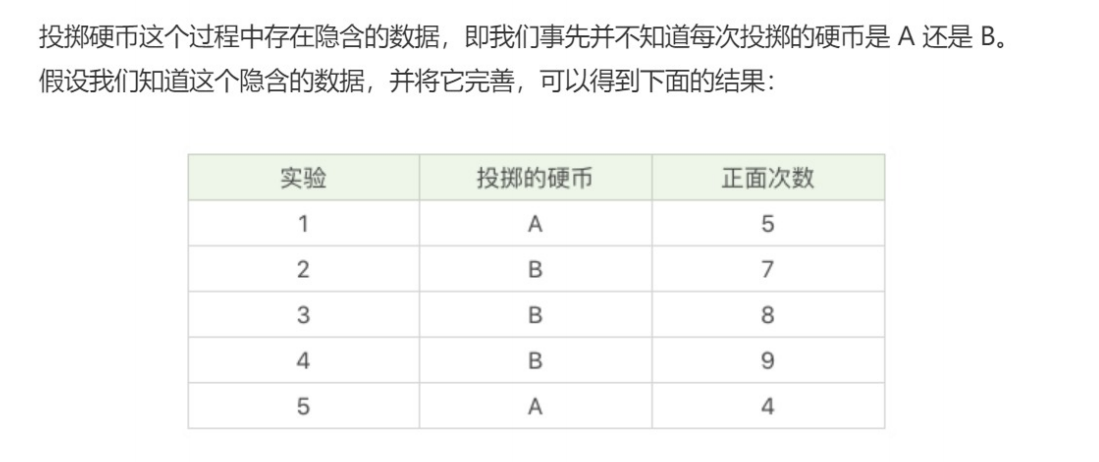



EM聚类的工作原理
就是把潜在类别当做隐藏变量,样本看做观察值,就可以把聚类问题转化为参数估计问题。这也就是EM聚类的原理
相比于K-means算法,EM聚类更加灵活,因为K-means是通过距离来区分样本之间的差别的,且每个样本在计算的时候只能属于一个分类,称之为硬聚类算法,而EM聚类在求解的过程中,实际上每个样本都有一定的概率和每个聚类相关,叫做软聚类算法
EM算法可以理解成一个框架,在这个框架中采用了不同的模型来用EM进行求解。常用的EM聚类有GMM高斯混合模型和HMM隐马尔科模型。
一般我们可以假设样本是符合高斯分布的,每个高斯分布都属于这个模型的组成部分,要分成K类就相当于是K个组成部分。这样我们可以先初始化每个组成部分的高斯分布的参数,然后再看来每个样本是属于哪个组成部分,这也就是E步骤,再通过得到的这些隐含变量结果,反过来求每个组成部分高斯分布的参数,既M步骤。反复EM步骤,直到每个组成部分的高斯分布参数不变为止
总结
EM聚类和K-means聚类的相同之处和不同之处
相同点:
- EM,K-means,都是随机生成预期值,然后经过反复调整,获取最佳结果
- 聚类个数清晰
不同点:
- EM是计算概率,K-means是计算距离
- 计算概率,概率只要不为0,都有可能既样本是每一个类别都有可能
,K-means是计算距离 - 计算概率,概率只要不为0,都有可能既样本是每一个类别都有可能
- 计算距离,只有近的才有可能,既样本只能属于一个类别