动手学深度学习笔记1
关于本书数字:
- 标量可以看作0维张量
- 向量可以看作1维张量
- 矩阵可以看作2维张量
- 张量可以看作一个多维数组
关于本书函数和运算符
- 指示函数是定义在某集合X上的函数,表示其中有哪些元素属于子集A。
- 点乘,首先保证矩阵的结构相同,再把对应位置的数值相乘。
- 集合的基数,是指集合元素的个数(也成为集合的势)
- Lp正则
- L2正则
正则化:对某一问题加以先验的限制或约束以达到某种特定目的的一种手段或操作。在算法中使用正则化的目的是防止模型出现过拟合*。
- 点积:即内积
1.1日常生活中的机器学习
概念定义
- 参数:可以看作旋钮,可以转动它来调整程序的行为。
- 模型:任一调整参数的程序后。
- 模型族:通过操作参数生成不同程序(输入-输出映射)的集合。
- 学习算法:使用数据集来选择参数的元程序
- 学习:在机器学习中,学习(learning)是一个模型的训练过程。
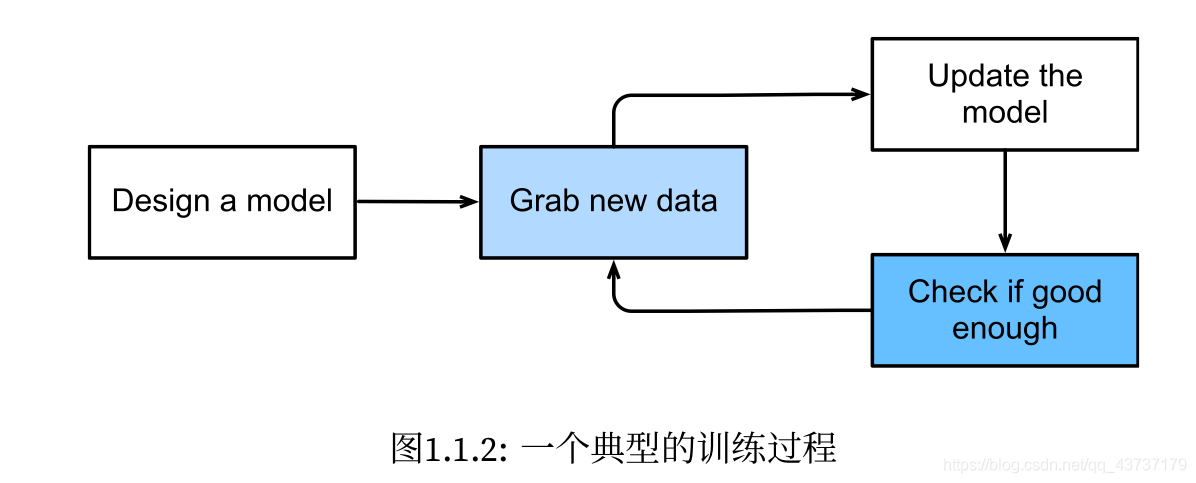
训练过程通常包含以下步骤:
- 从一个随机初始化参数的模型开始,这个模型基本毫不智能。
- 获取一些数据样本
- 调整参数,使模型在样本中表现的更好
- 重复2,3,直到模型的结果令人满意。
1.2关键组件
1.2.1数据(data)
数据集由数个样本组成,样本也可以称为数据点或数据实例。而每个样本由一组称为特征(或协变量)的属性组成。有时候特征也可以被称为标签或者目标。
e.g.处理的是图像数据时,每张照片是一个样本,它的特征由每个像素数值的有序列表表示。例如,一张200×200的彩色图片是由200×200×3=120000个数值组成的,其中3对应的是每个位置的RGB通道强度。
1.2.2模型(model)
深度学习与经典方法的区别主要在于,前者关注的功能强大的模型,这些模型由神经网络错综复杂的交织在一起,包含层层数据转换,因此被称为深度学习。
1.2.3目标函数(The objective function)
目标函数是指在机器学习中用于定义模型的优劣程度的度量。
通常我们定义一个目标函数,并希望优化到它的最低点,也因此有时候这些函数被称为损失函数(loss function/cost function),但同样的我们也可以定义其并希望优化到它的最高点。本质上是一样的。通常损失函数是根据模型参数定义的,并取决与数据集。
过拟合:在训练集上表现好,但在测试集上表现很差(即过分贴合训练集)
1.2.4优化算法
在深度学习中,大多流行的优化算法通常基于一种基本方法——梯度下降(gradient descent)。即在每个步骤中,梯度下降法都会检查每个参数,,如果你仅对某参数进行少量变动,那么训练集损失就会朝哪个方向移动,然后在可以减少损失的方向上优化参数。
1.3各种机器学习问题
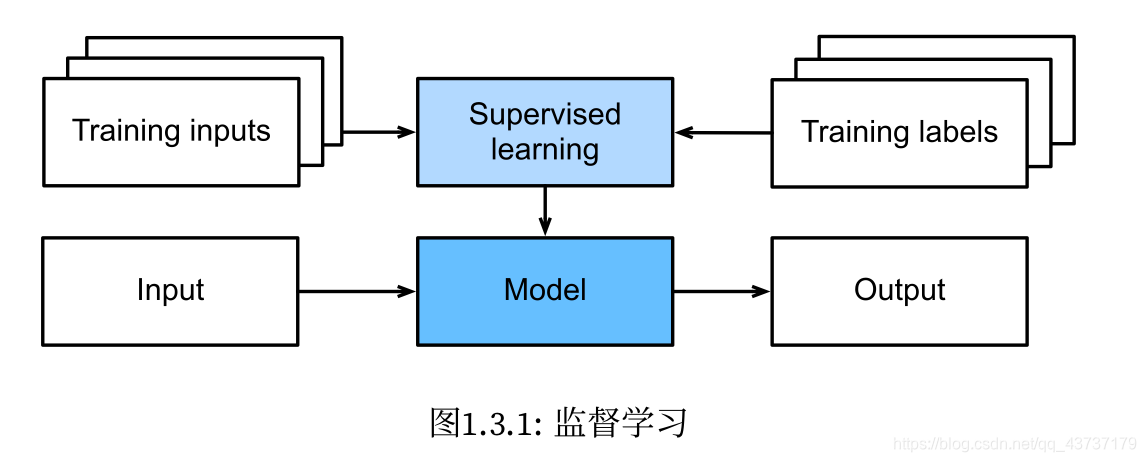
1.3.1监督学习(supervised learning)
监督学习是指在“给定输入标签”的情况下预测标签,具有明确的目标。
回归
回归是最简单的监督学习任务之一。
Note1: 如何归类问题属于回归问题本质上是由输出决定的。回归是我们预测一个具体的数值输出,分类是我们预测离散值输出。
在回归问题中,我们主要关注最小化平方误差损失函数。
分类
在分类问题中,我们希望模型能够预测样本属于哪个类别,最简单的分类问题是只有两类,称之为“二元分类”,在分类问题中,常见损失函数被称为交叉熵(cross-entropy)。
在分类问题中,我们将预期风险作为损失函数,也就是说我们需要将结果的概率乘以与之相关的收益(或者伤害)。
例如假设根据我们的毒蘑菇检测分类得出一个蘑菇是毒蘑菇的概率是0.2,那么食用它造成的损失是0.2×∞+0.8×0=∞,而丢弃蘑菇的损失是0.2×0+0.8×1=0.8。
标记问题
学习预测不互相排斥的类别的问题称为多标签分类,也就是标记问题。
搜索
对于信息检索,我们希望在海量的信息中得到我们最需要的那部分,显然,在海量的信息中我们将得到的不止一个信息,因此最终搜索结果的排序也是非常重要的。那么怎样排序呢?一种方法是对搜索结果集合中的每个元素给出相应的相关性分数,如何检索结果的排序依次由分数高低决定。
推荐系统
即个性化推荐
序列学习
序列学习的实例:假设我们用一个模型来监控重症监护病人,如果他们在未来24小时内死亡的风险超过某一个阈值,这个模型就会发出警报。显然我们不希望抛弃过去每小时与病人病史有关的信息。
序列学习需要摄取输入序列或预测输出序列,或者两者兼之。即输入和输出都是可变长度的序列。
标记和解析 输入和输出的数量基本上相同,涉及到用属性注释文本序列。
自动语音识别 输入序列是说话人的录音,输出序列是说话人所说内容的文本记录,难点在于音频与文本之间不是1:1的对应关系。
文本到语音 输入是文本,输出是音频文件
机器翻译 在机器翻译中,颠倒输入和输出的顺序非常重要。
1.3.2 无监督学习(unsupervised learning)
数据中不含有目标的机器学习问题称为无监督学习
- 聚类问题:没有标签的情况下能否给数据分类?
- 主成分分析问题:能否找到少量的参数来准确地捕捉数据的线性相关属性
- 因果关系和概率图模型:能否描述观察到的许多数据的根本原因
- 生成对抗性网络:提供一种合成数据的方法
1.3.3 与环境互动
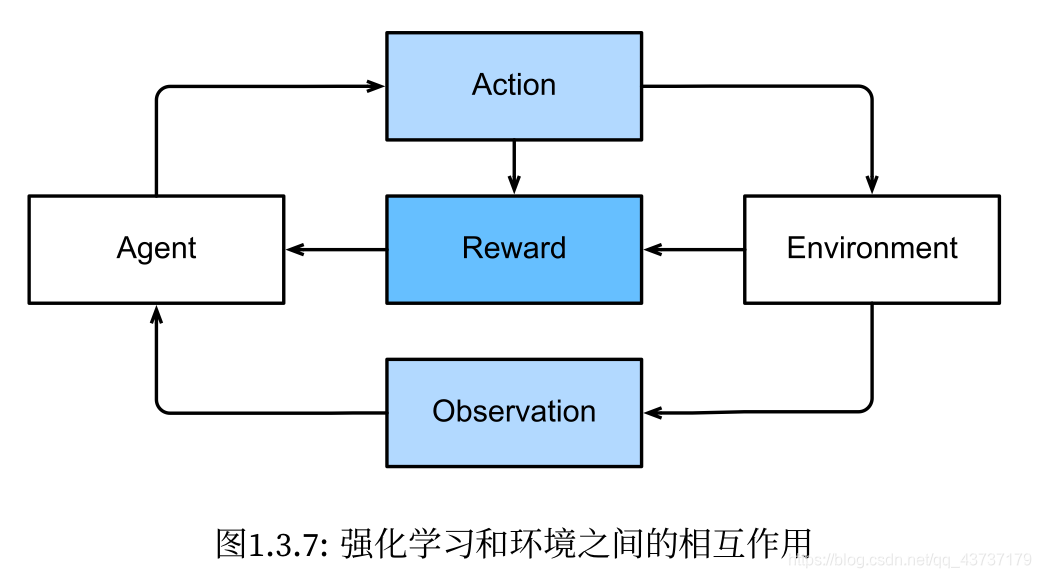
1.3.4 强化学习(reinforcement learning)
强化学习的目标是产生一个好的策略,在强化学习问题中,agent在一系列的时间步骤上与环境交互,在每个特定时间点,agent从环境接收一些观察(observation),并且必须选择一个动作(action),然后通过某种机制将其传输回环境,最后agent在环境中获得奖励(reward)。
当环境可以被完全观察到时——马尔科夫决策过程
当状态不依赖于之前的操作时——上下文赌博机
当没有状态,只有一组最初未知回报的可用动作时——多臂赌博机
1.4 起源(略)
- 线性和非线性处理单元的交替,通常成为层(layers)
- 使用链式规则(即反向传播)一次性调整网络中的所有参数。
1.5 深度学习之路
- 新的容量控制方法,如dropout,有助于减轻过拟合的危险,是通过在整个神经网络中应用噪声注入来实现的,出于训练母的,用随机变量来代替权重。
- 注意力机制解决了:如何在不增加可学习参数的情况下增加系统的记忆和复杂性。
- 多阶段设计:允许统计建模者描述用于推理的迭代方法。
- 生成对抗网络:其关键创新是用具有可微参数的任意算法代替采样器,然后对这些数据进行调整,使得鉴别器(即对两个样本的测试)不能区分假数据和真实数据。
- 并行计算能力
- 深度学习框架
1.6 成功案例
- 智能助理
- 数字助理
- 物体识别
- 游戏
- 自动驾驶
1.7