[人工智能]强化学习与数学

参考文献:
$[1]\mathcal{A}gent57:\mathcal{O}utperformingthe\mathcal{A}tari\mathcal{H}uman\mathcal{B}enchmark$
$[2]\mathcal{R}enforcement\mathcal{L}earning(\mathcal{S}utton)$
文献[1]的附录对我而言是比其本体更有用的资料，它从数学推导的角度一步步地告诉我们强化学习的进化历程。尽管我大部分的知识都是源自于文献[2]，但是读一本百千页的书是相当辛苦的事情，尤其是太过详细的那种，而且由于长时间未涉及到RL相关的内容，我感觉一些知识已经遗忘，所以本文以[1]为重点，试图去顺一顺RL的历程。

Markov Decision Process

马尔科夫决策链过程可以被描绘为$(\mathcal{X},\mathcal{A},\mathcal{P},r,y)$, 就像物理坐标系中的$(t,x,y,z)$一样，马尔科夫链描绘的是一个事件。接下来介绍一下每一个变量的含义：
$\mathcal{X}$: 状态空间
$\mathcal{A}$: 动作空间
$\pi$ : 状态空间转移时需要依据，这种依据我们称之为策略。
$\mathcal{P}$: $P(x^{\prime }|a,x)$这个意味着在状态$x$下采取行动$a$，从而转移到状态$x^{\prime }$的概率.
$r$ : $r\in {\mathbb{R}}^{\mathcal{A}\times \mathcal{X}}$
$y$: $y\in [0,1]$
ok，有了着一些前提条件以后我们就可以引入价值函数的概念了。

State-Action Value Function

$\tau (x,a,\pi )$是迹$\tau =(X_t,A_t,R_t,X_{t+1}{)}_{t\in \mathbb{N}}$中根据$\pi$的一个分布，然后其中各个属性之间有如下关系:$?t>=1,R_t=r(X_t,A_t),\&?t>=0,X_{t+1}P(?|X_t,A_t)$,状态-行动价值函数(state-action value function)可以和描述为$Q_r^{\pi }=E_{{}_{\tau }～\tau (x,a,\pi )}[{\sum }_{t>=0}{R}_t]$
最优状态的价值函数也就是$Q_r^{?}(x,a)={\max }_{\pi }{Q}_r^{\pi }(x,a)$意思就是找到一个策略函数使得整体获得的价值最大化。

Bellman equation

我们观察某一个transition的状态，根据价值函数，我们知道每一个transition势必将涉及到一个reward，长时积累reward将会令价值函数趋于无穷大，无穷大不是一件好事情，所以我们需要对以前所积累的reward做一个衰减，也就是在每一个加奖赏值之前都需要对以往积累的价值乘个衰减因子$y$。这样，一步Bellman方程可以描绘为:
$T_r^{\pi }Q(x,a)=r(x,a)+y{\sum }_{b\in \mathbb{A}}{\sum }_{x^{\prime }\in x}\pi (b|x)P(x^{\prime }|x,a)Q(x^{\prime },b)$
看到上面的公式你可能会有很多疑惑，为何左边是两个代数相乘，右边则找不到公共因子。我认为左边应该类似于复合函数的写法，但是我尚未统计其他资料中数学公式的写法，这也有可能是作者自己创造的书写形式。
这个公式是怎么来的呢？引入了衰减因子以后，传统的价值函数可以被写为类似于:$Q(x,a)=E[r_0+y{r}_1+y^2{r}_2+???+y^{n?1}{r}_{n?1}]$
$\to r_0+E[y{r}_1+y^2{r}_2+???+y^{n?1}{r}_{n?1}]$
$\to r_0+\sum y^i{r}_i=r_0+y\sum y^{i?1}{r}_i=r_0+yQ(x_{t?1},a_{t?1})$
这个时候还没结束，我们知道每一状态转移都会涉及到策略$\pi$以及概率$P$所以对于每一个价值函数$Q$,我们还需乘以策略$\pi$以及概率$P$,最终我们得到了Bellman方程的形式$T_r^{\pi }Q(x,a)=r(x,a)+y{\sum }_{b\in \mathbb{A}}{\sum }_{x^{\prime }\in x}\pi (b|x)P(x^{\prime }|x,a)Q(x^{\prime },b)$.

贪心算法(Greedy Policy)

顾名思义每一次决策都奔着奖赏最大化去。

Transformed Bellman Operators

$?z\in \mathbb{R},h(z)=sign(z)(\sqrt{|z|?1})+\epsilon z$
$?z\in \mathbb{R},h(z{)}^{?1}=sign(z)(\frac{\sqrt{1+4\epsilon (|z|+1+\epsilon )}?1}{2\epsilon })z$

$T_r^{\pi }Q(x,a)=h(r(x,a)+y{\sum }_{b\in \mathbb{A}}{\sum }_{x^{\prime }\in x}\pi (b|x)P(x^{\prime }|x,a)h^{?1}(Q(x^{\prime },b)))$.

论文中描述说这种变换形式更容易让神经网络去拟合。

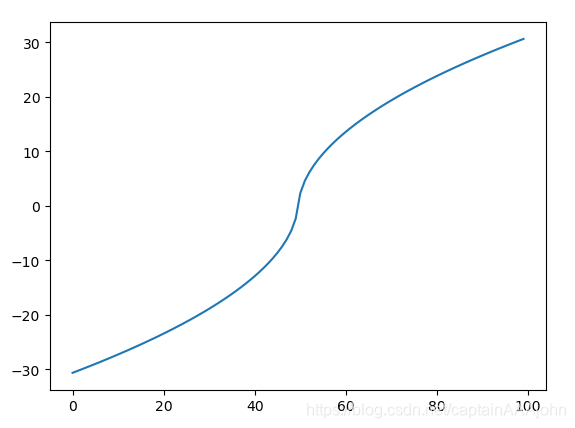
如图所示，我绘制了定义域位于-1000到1000之间的函数，可以分析得到，这个函数具备挤压函数的性质，同时并没有sigmoid那种梯度消失的缺点，因为当输入很大时所得到数值仍具备一定增长趋势。
为了方便后续的介绍，我们引入一些符号进行定义：
对于贪心策略:${\pi }_k=\mathcal{G}(Q_k)$
前一步价值函数和后一步价值函数之间的联系可以被描绘为:$Q_{k+1}=T_{r,h}^{{\pi }_k}{Q}_k$其中各个下角标我们在上文已经详细描绘过了。

Intrinsic-Extrinsic Decomposition

上文中所作的讨论是在仅仅一种reward的情况下，但是现实中内在和外在的因素都是至关重要的，比如有一个汉堡看起来很好吃，我们的感官是内在因素而自己手里的钱以及排队人数等等是外在因素。所以我们需要将内在外在因素都考虑在内。
通过将内在的奖励和外在的奖励进行线性组合我们得到了价值函数的新的表现形式$Q=Q^i+\beta Q^e$其中$\beta$是$Q^e$相对于$Q^i$的权重。
这样的话，该系统的策略就变成了${\pi }_k=\mathcal{G}(Q_k^e+Q_k^i)$
然后基于这个新的${\pi }_k$我们分别对$Q_k^e$以及$Q_k^i$进行更新。
下面对奖赏函数的可拆分组合性进行简单地证明:
$Q_{k+1}=Q_{k+1}^i+\beta Q_{k+1}^e$
$\to T_{r^i}^{{\pi }_k}{Q}_k^i+r_k^i+(T_{r^e}^{{\pi }_k}{Q}_k^e+r_k^e)\beta$
$\to (r_k^i+\beta r_k^e)+(T_{r^i}^{{\pi }_k}{Q}_k^i+T_{r^e}^{{\pi }_k}{Q}_k^e)$
$\to r_k+T_r^{{\pi }_k}{Q}_k$
在上文提及到的压缩函数应用到上式中仍然成立。

Retrace and transformed Retrace

时序差分(TD)

上文中我们提到了$Q(x,a)=r(x,a)+y\sum \sum Q(x^{\prime },b)P(x^{\prime }|x,a)\pi (x^{\prime }|b)$这是一种动态规划方法。
在蒙特卡洛方法中一般是从一个eposide中进行采样，然后根据$Q(x)=Q(x)+a(Gt?Q(x))$
将动态规划和蒙特卡洛相结合后我们就得到了TD方法:$Q(x)=Q(x)+a(r+yQ(x^{\prime })?Q(x))$
$(r+yQ(x^{\prime })?Q(x)$这一部分我们使用$\delta$进行代替。
在论文中还引入了其他trick从而将全时间范围内的TD考虑进了系统中。
$\text{trick}$ 根据策略函数预测势必同真实分布之间存在一点点区别。为了让模型的预测环境由真实分布转向为策略分布，对每一个TD都需要乘以一个系数这个系数为$\frac{\pi }{u}$其中$u$对应着统计数据，也就是将所有的情况收集起来，用对应transition的数目除以所有transition的数目从而得到一个平均分布。真实情况下还需要做一个变换$c_s=\lambda \min (1,\frac{\pi (A_s|X_s)}{A_s|X_s})$,意思是这个比值不可超过1，同时经过一个线性变换系数$\lambda$(位于[0,1])进行适当地放缩。
PS：$u$和$\pi$区别在，当你设计随机性时，$u$中的数据并不完全是$\pi$得到的，同时每一个决策同下一个决策存在着联系，所以只要是有随机性，$u$和$\pi$将会是不相同的分布。
基于此作者在论文中作者给出了一个更全面的TD: $T_r^{u,\pi }=E_{r～\tau (x,a,u)}[Q(x,a)+\sum y^t(\prod c_s){\delta }_t]$
如果用一句话来描述的话，这个公式是一个放缩因子为$y$的从时刻为0开始评价的并且带有策略纠正的时序差分。

Transformed

上文中我们提及了一种挤压函数，并将其应用在了$Bellman$方程中。同理，挤压函数也可以应用在TD中作者给的公式为:
$T_{r,h}^{u,\pi }Q(x,a)=h(E_{{}_{\tau }～\tau (x,a,h)}[h^{?1}(Q(x,a)+\sum _{t>=0}{y}^t(\prod _{s=1}^t{c}_s){\delta }_t^h)])$
${\delta }_t^h=r_t+y\sum a\in A\pi (a|X_{t+1})h^{?1}(Q(X_{t+1},a))?h^{?1}(Q(X_t,A_t))$
看起来很复杂，其实就两个要点将公式中各个价值函数替换为压缩函数逆变化，而整体则直接使用压缩函数进行变换。

Extrinsic-Intrinsic Decomposition for Retrace and Transformed Retrace

对于TD形式下的价值函数，我们仍然可以根据内在外在的奖励将各类价值拆分计算后组合。
同时利用挤压函数进行变换，也是没有问题的。
将内在外在奖励分开计算并使用挤压函数做非线性处理以后可得:
$\pi =\mathbb{G}(h(h^{?1}(Q_k^e)+b{h}^{?1}(Q_k^i)))$
$Q_{k+1}^i=T_{r^i,h}^{u_k,{\pi }_k}{Q}_k^i$
$Q_{k+1}^e=T_{r^i,h}^{u_k,{\pi }_k}{Q}_k^e$

Retrace and transformed Retrace Losses for Neural Net

上文我们介绍了一种基于TD去求价值函数的方法。
下文中的公式基于TD：$Q_{k+1}=\underset{Q\in {\mathbb{R}}^{x\times \mathcal{A}}}{\mathrm{argmin}}||T_r^{u,\pi }{Q}_k?Q||$，norm中右边一项是TD所得，左边一项是真实的价值函数。
$A\times X$可能是一个很大的空间，因此使用神经网络去拟合这个空间可以有效地节约资源这一种方法也被称作(online model)。
在实际操作中使用两个network，一个network（叫做target network）用来描述右边的价值函数（一些人也将这个网络称作评价网络），另外一个用来计算TD（value network）。
network的设计思想是统一的即$Q(x,a|\theta )$通过参数中储存的知识计算当前状态x下选择a的价值。但这两种network的参数是不同的。
我们可以看到$Q_{k+1}=\underset{Q\in {\mathbb{R}}^{x\times \mathcal{A}}}{\mathrm{argmin}}||T_r^{u,\pi }{Q}_k?Q||$类似于一种MSE的形式，因此这个目标函数可以通过梯度下降去优化。
在这个目标函数中，也可以应用挤压函数，其代数形式为:$Q_{k+1}=\underset{Q\in {\mathbb{R}}^{x\times \mathcal{A}}}{\mathrm{argmin}}||T_{r,h}^{u,\pi }{Q}_k?Q||$。目标网络未使用挤压函数的原因是$f{f}^{?1}(z)=z$.