1.吴恩达机器学习第一章课程笔记

1.1 机器学习的定义

在这里插入图片描述
根据Samuel的定义，机器学习是使电脑有能力根据数据集学习，而不是根据每个样本的不同而人工编程。

根据Mitchell的定义，机器学习是通过在任务T（task）上的表现P（performance）的测定而获得经验E（experience),获得E越多，机器学习的能力会越强。

一个小的测试题：若邮箱垃圾过滤器学习了人工是否将邮件分类为垃圾软件，并基于此，学习成为更优秀的过滤器，在选项中哪一项是T（Task）。
在这里插入图片描述
观察人工标签邮件是否为垃圾邮件是步骤E，过滤器将邮件分类是步骤T,正确的分类数目是步骤P。

1.2 监督学习

在这里插入图片描述
机器学习的算法包括监督学习和非监督学习，还包括强化学习和推荐算法。

监督学习简单来说就是算法通过观察分类的结果，从而机器习得这类算法；或是通过给定的数据集（包含正确的回答），做出拟合的函数或是分界线，从而预测数据点所对应的结果。

来看一个预测房价的例子（regression）：
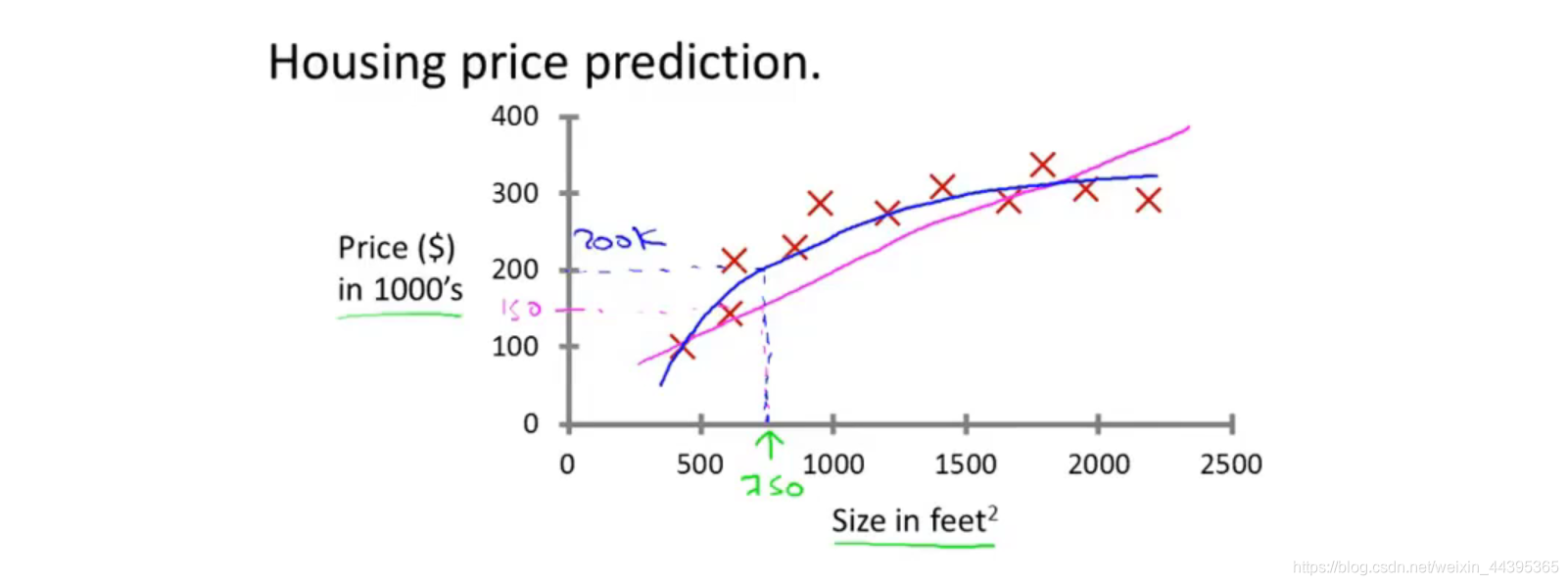
在这里插入图片描述
显示的是面积和房价的数据点，红色是正确的点，粉色是拟合直线，机器用拟合直线来判断预测点的房价。

来看一个肿瘤的特征与肿瘤良性/恶性的例子（classification）：
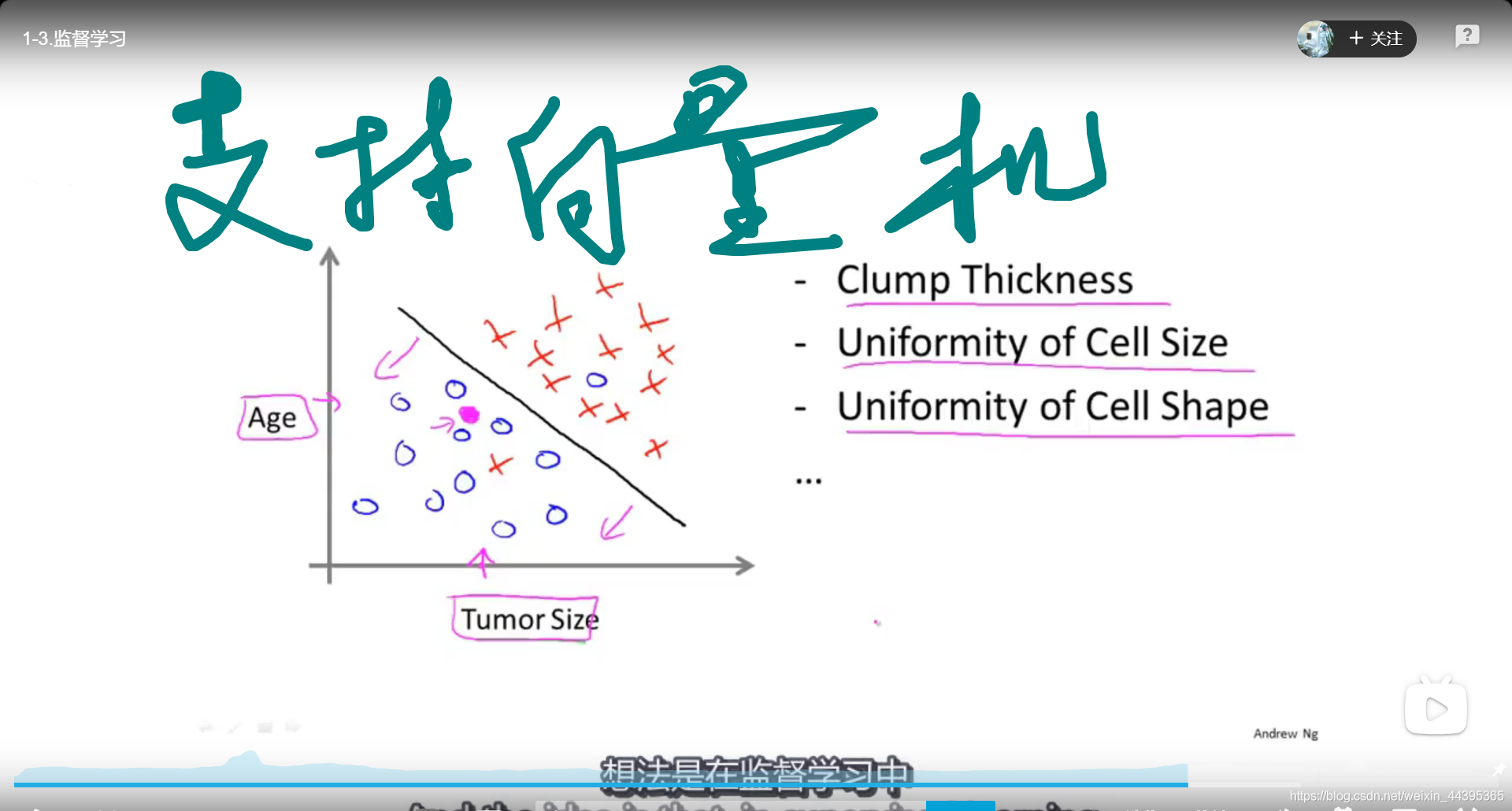
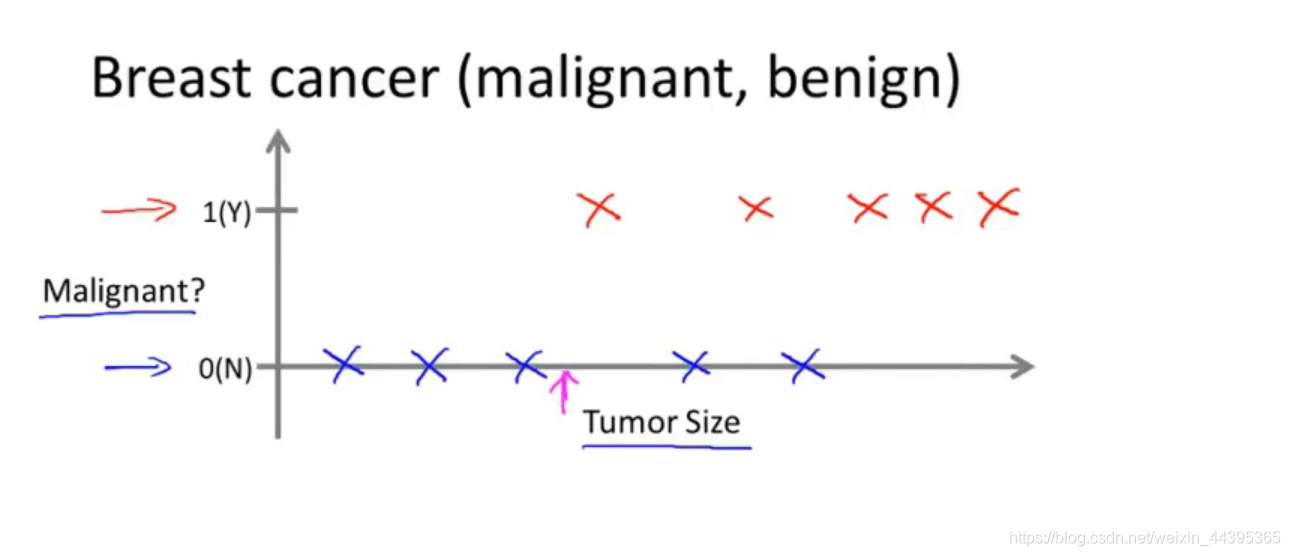
在这里插入图片描述

第二张图蓝色表示良性，红色表示恶性，我们从第二张图可以看出，随着肿瘤越变越大，恶性的概率越来越高；第一张图同时考虑了患者的年龄大小，这时，学习算法可能会给出类似黑色的分界线来区分是良性还是恶性。

在现实情况下，还会有更多考量的因素，比如肿瘤的厚度、病变区域细胞的大小、性质的一致性等，我们可以使用支持向量机(SVM)（在计算机视觉章节中有实现过算法）。

监督学习可以分为两类：回归（regression）,预测连续值的输出；分类（classification），预测离散值的输出。

一个小问题（回归和离散的判断）：
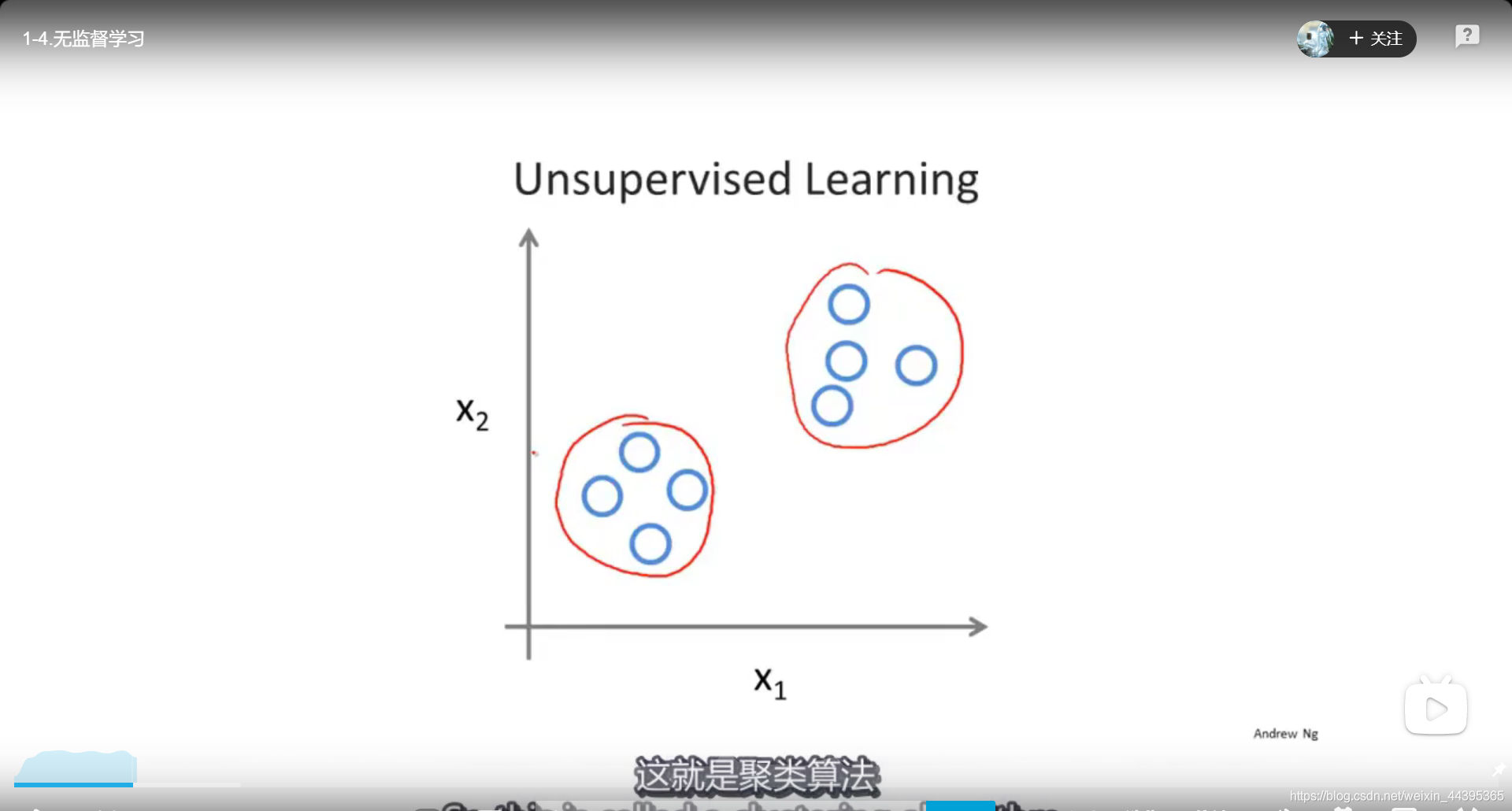
在这里插入图片描述

1.3 无监督学习

无监督学习简而言之就是未给出数据的标签，让机器通过观察，自动将“簇”进行分类，聚类型问题属于无监督学习的一种。
无监督学习的应用：
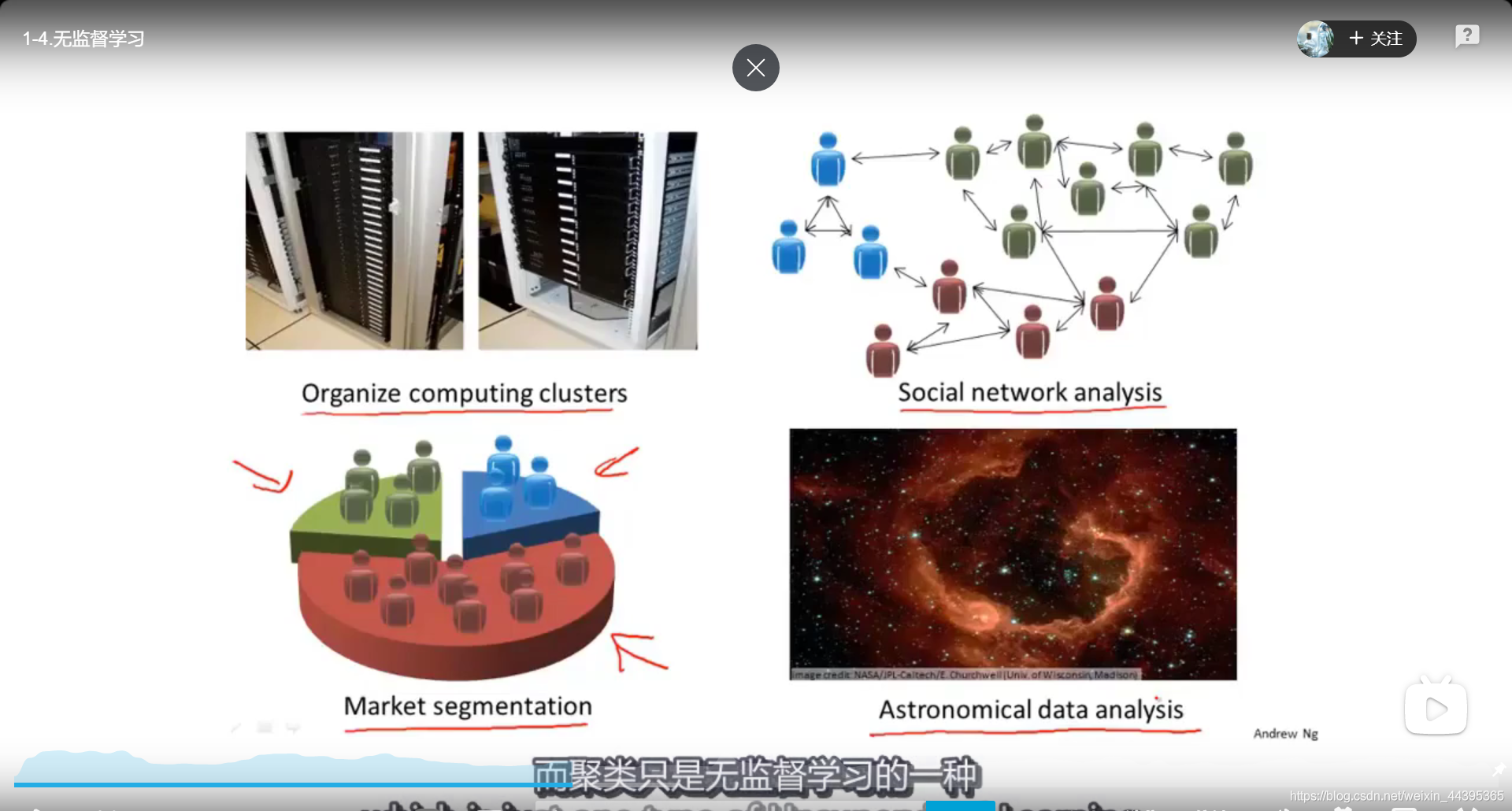
在这里插入图片描述

一个小问题：

2.周志华机器学习第一章

2.1 基本术语

本章举了西瓜的例子，比如（色泽=青绿；根蒂=蜷缩；敲声=浊响）等，这样记录的集合称为“数据集”，每条记录称为一个“示例”或“样本”，色泽、根蒂、敲声称为“属性”或“特征”，青绿、乌黑、浊响称为“属性值”。属性张成的空间称为“属性空间”、“样本空间”或“输入空间”。我们把“色泽”、“根蒂”、“敲声”作为三个坐标轴，每个西瓜都可以在空间中找到坐标位置，由于空间每个点对应一个坐标向量，因此也把示例称为“特征向量”。

令 $D=\lbrace x_1,x_2,...x_m \rbrace$ 表示包含m个示例的数据集，每个示例由d个属性描述。 $x_i= \lbrace x_{i1};x_{i2};...,x_{id} \rbrace$ 是d维样本空间 $\chi$ 中的一个向量。 $x_{ij}$ 是 $x_i$ 在第j个属性上的取值。

从数据中学得模型的过程称为学习或训练,这个过程通过执行学习算法来完成，训练过程中使用的数据称为训练数据，样本称为训练样本，组成的集合称为训练集。

为习得一个能够判断是不是“好瓜”的模型，需获得训练样本的“结果”信息（什么样属性空间的瓜是好瓜），“好瓜”称为“标记”（label),拥有标记信息的示例，称为“样例”。一般用 $x_i,y_i)$ 表示第i个样例， $y$ 是标记， $\gamma$ 是所有标记的集合，亦称为“标记空间”。

若预测的是瓜的好坏，预测的是离散值，学习任务称为分类（classification）;若预测的是连续值，如西瓜的成熟度，此学习任务称为“回归”（regression)。

习得模型之后，及逆行预测的过程称为“测试”。

我们还可以对西瓜做“聚类”（clustering），即将训练集中的西瓜分成若干组，每组称为一个“簇”，簇对应一些潜在的概念划分，例如“浅色瓜”，“深色瓜”，甚至“本地瓜”，“外地瓜”等，不拥有标记信息，是无监督学习的一种。

通常假设样本空间中全体样本服从一个未知“分布” $D$ ，每个样本都是“独立”地从分布上获得地，即“独立同分布”，训练样本越多，得到关于D地信息越多，越有可能通过学习获得具有强泛化能力的模型。

2.2 假设空间

归纳和演绎是科学推理的两大基本手段，前者是从特殊到一般的“泛化”，即从具体的事实归纳出一般性规律；后者则是从一般到特殊的“特化”过程，即从基础原理推演出具体状况。

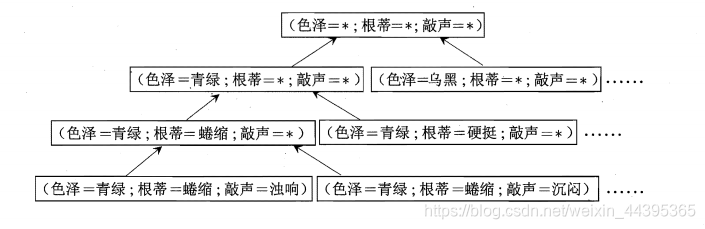
概念学习中最基本的是布尔概念学习，即对“是”或“不是”这样的可表示为0/1布尔值的目标概念的学习。比如下图：
在这里插入图片描述
布尔表达式：“好瓜 $\leftrightarrow$ (色泽=?) ^ (根蒂=?) ^ (敲声=?)” ?表示未确定的取值。

我们可以把学习过程看作一个在所有假设（hypothesis）组成的空间中进行探索的过程，搜索目标是找到与训练集匹配的假设，假设的表示一旦确定，假设空间及规模大小也就确定了。用“*”（通配符）表示某个属性中无论取什么值都合适，此外，也要考虑极端情况，“好瓜”这个概念根本不存在，用 $\emptyset$ 来表示。

假设色泽、根蒂、敲声分别有3、2、2种可能取值，假设空间的大小为 $(3+1)\times(2+1)\times(2+1)+1=37$

在这里插入图片描述

2.3 归纳偏好

对具体的学习算法而言，它必须要产生一个模型，学习算法本身的“偏好”会起到关键的作用，称为“归纳偏好”。

例如，若认为相似的样本有相似的输出（在各种属性上都很相像的西瓜），成熟程度应比较接近，对应的算法可能偏好平滑的曲线A而不是“崎岖”的曲线B。

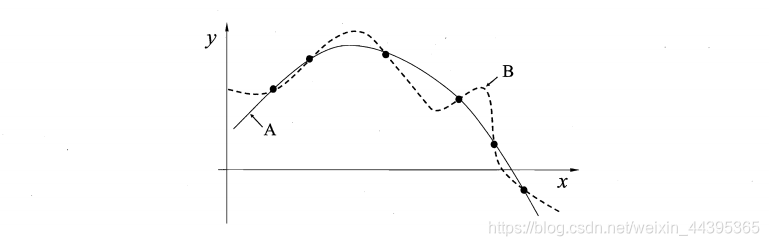
在这里插入图片描述
事实上，归纳偏好对应了学习算法本身所做出的关于“什么样的模型更好”的假设，在具体现实问题中，这个假设是否成立，即算法的归纳偏好是否与问题本身匹配，大多数时候直接决定了算法能否取得更好的性能。

偏好要结合问题本身，没有平滑简单的曲线性能比“崎岖”、属性值更一般的曲线性能更好这种说法。
在这里插入图片描述
假设样本空间 $\mathcal{X}$ 和假设空间 $H$ 都是离散的，令 $P（h|X,\xi_{a}）$ 代表算法基于训练数据X产生假设h的概率，再令f代表算法的“训练集外误差”，算法在训练集之外的所有样本上的误差为：

若为真，则表示假设与实际情况不同。P（x）代表样本中各样本的概率。