[人工智能]聚类模型

聚类模型

聚类就是将样本划分为由类似的对象组成的多个类的过程。聚类后，我们可以更加准确的在每个类中单独使用统计模型进行估计、分析或预测也可以探究不同类之间的相关性和主要差异。聚类和分类的区别是分类是已知类别的，聚类未知。

K-means聚类算法

• 步骤

1. 指定需要划分的簇的个数K值（类的个数）
2. 随机地选择K个数据对象作为初始的聚类中心（不一定要是样本点）
3. 计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中。
4. 调整新类并且重新计算出新类的中心。（通常是重心）
5. 循环步骤三和四，看中心是否收敛（不变），如果收敛或达到迭代次数则停止循环。
6. 结束。

• 优点

1. 算法简单、快速。
2. 对处理大数据集，该算法是相对高效率的。

• 缺点

1. 要求用户必须事先给出要生成的簇的数目K。
2. 对初值敏感。
3. 对于孤立点数据敏感。

K-means++聚类算法

初始的聚类中心之间的相互距离要尽可能的远。

• 步骤

1. 随机选取一个样本作为第一个聚类中心。
2. 计算每个样本与当前已有聚类中心的最短距离（即与最近一个聚类中心的距离），这个值越大，表示被选取作为聚类中心的概率较大。最后，用轮盘法（依据概率大小来进行抽选）选出下一个聚类中心。
3. 重复步骤二，直到选出K个聚类中心。选出初始点后，就继续使用标准的K-means算法了。

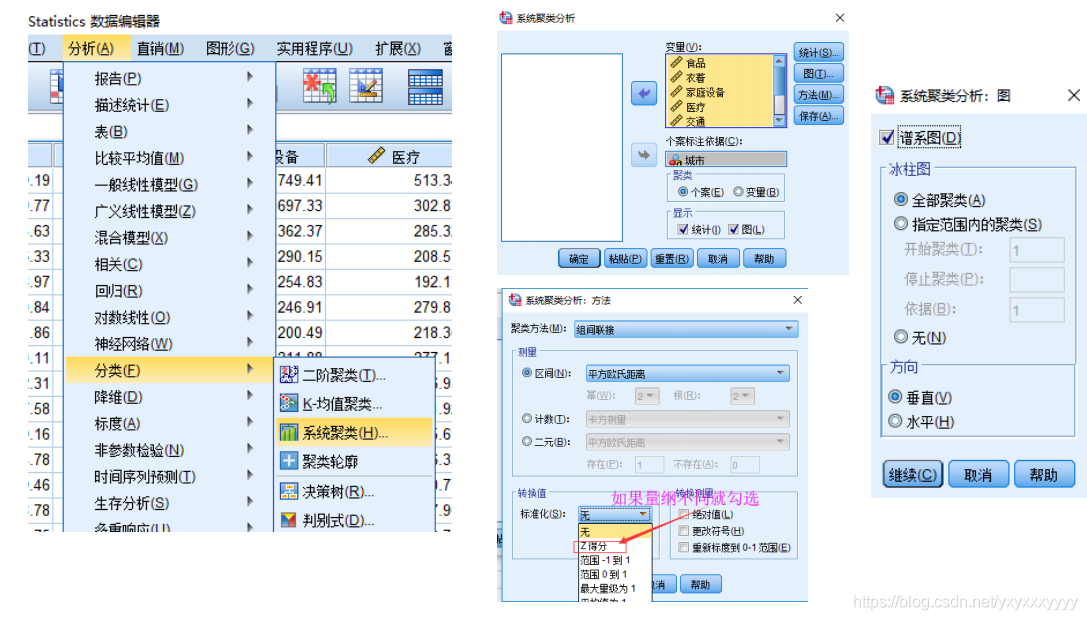
• 使用SPSS
  
  处理量纲不一致的方法 ：标准化$z_i=\frac{x_i?\bar{x}}{{\sigma }_x}$
  
  

系统（层次）聚类

• 步骤

1. 将每个对象看作一类，计算两两之间的最小距离。
2. 将距离最小的两个类合并成一个新类。
3. 重新计算新类与所有类之间的距离。
4. 重复二三两步，直到所有类最后合并成一类。
5. 结束。

• 距离问题

  • 样本与样本之间的距离
    
  • 指标与指标之间的距离
    
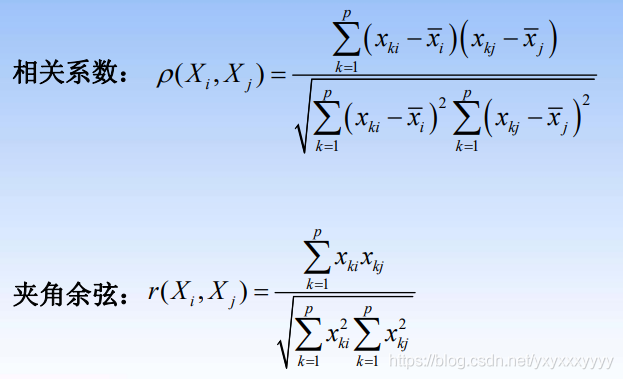
  • 类与类之间的常用距离
  1. 最短距离法(Nearest Neighbor)
     
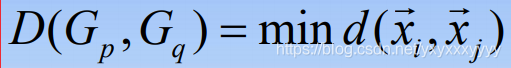
  2. 最长距离法(Furthest Neighbor)
     
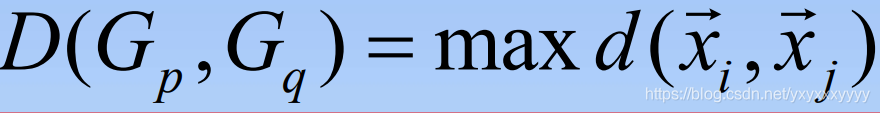
  3. 组间平均连接法(Between-group Linkage)
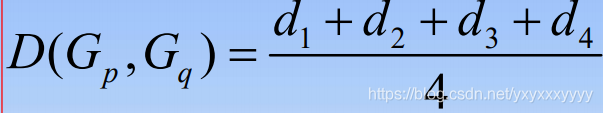
  4. 组内平均连接法(Within-group Linkage)
     
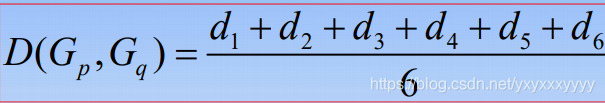
     5.重心法(Centroid clustering)
     

• Spss软件操作
  

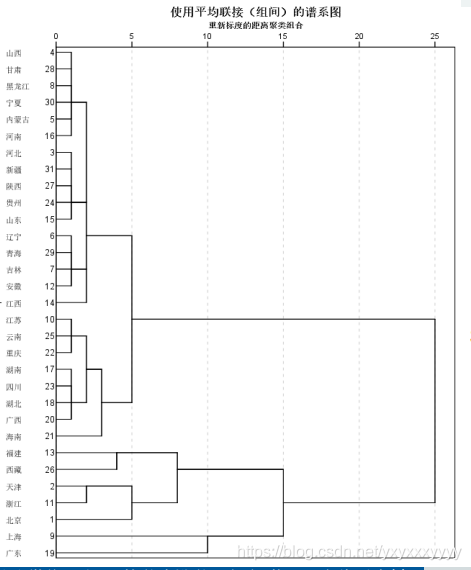
• 聚类谱系图（树状图）

• 用图形估计聚类的数量

  • 肘部法则（Elbow Method）：通过图形大致的估计出最优的聚类数量
    k越大，畸变程度越大。

• 聚合系数折线图的画法
  

1. 根据聚合系数折线图可知，当类别数为5时，折线的下降趋势趋缓，故可将类别数设定为5。
2. 从图中可以看出， K值从1到5时，畸变程度变化最大。超过5以后，畸变程度变化显著降低。因此肘部就是 $K=5$，故可将类别数设定为5。（当然，$K=3$ 也可以解释）

• 确定K后保存聚类结果并画图
  

DBSCAN算法

• 数据点分类

1. 核心点：在半径Eps内含有不少于MinPts数目的点
2. 边界点：在半径Eps内点的数量小于MinPts，但是落在核心
   点的邻域内
3. 噪音点：既不是核心点也不是边界点的点

• 例子
  
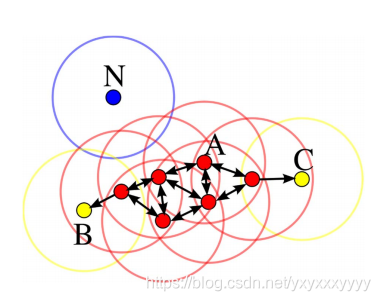
  在这幅图里，MinPts = 4，点 A 和其他红
  色点是核心点，因为它们的 ε-邻域（图中红色
  圆圈）里包含最少 4 个点（包括自己），由于
  它们之间相互相可达，它们形成了一个聚类。
  点 B 和点 C 不是核心点，但它们可由 A 经其
  他核心点可达，所以也和A属于同一个聚类。
  点 N 是局外点，它既不是核心点，又不由其他点可达。

• 伪代码
  

• 优点

1. 基于密度定义，能处理任意形状和大小的簇；
2. 可在聚类的同时发现异常点；
3. 与K-means比较起来，不需要输入要划分的聚类个数。

• 缺点

1. 对输入参数ε和Minpts敏感，确定参数困难；
2. 由于DBSCAN算法中，变量ε和Minpts是全局唯一的，当聚类的密度不均匀时，聚类距离相差很大时，聚类质量差。
3. 当数据量大时，计算密度单元的计算复杂度大

（推荐在观察变量长得不像“DBSCAN”时，全部使用系统聚类）

关注博主即可阅读全文