[人工智能]人工智能系列实验（三）——用于识别猫的二分类深度神经网络

本实验利用Python，搭建了一个用于识别猫的深度神经网络，最终实现在测试集上的准确率在80%以上。

本实验的任务目标、数据集等与人工智能系列实验（一）完全相同。神经网络框架则从实验一的单神经网络提升至本实验的深度神经网络，进而对比深度神经网络对预测性能的提升。

实验环境： python中numpy、matplotlib和h5py库

import numpy as np
import matplotlib.pyplot as plt  # 用于画图
import h5py  # 用于加载训练数据集

训练样本： 209张64*64的带标签图片

测试样本： 50张64*64的带标签图片

关于本实验中所用数据集与完整代码详见：
https://github.com/PPPerry/AI_projects/tree/main/3.cats_identification_dnn

构建的神经网络模型如下：

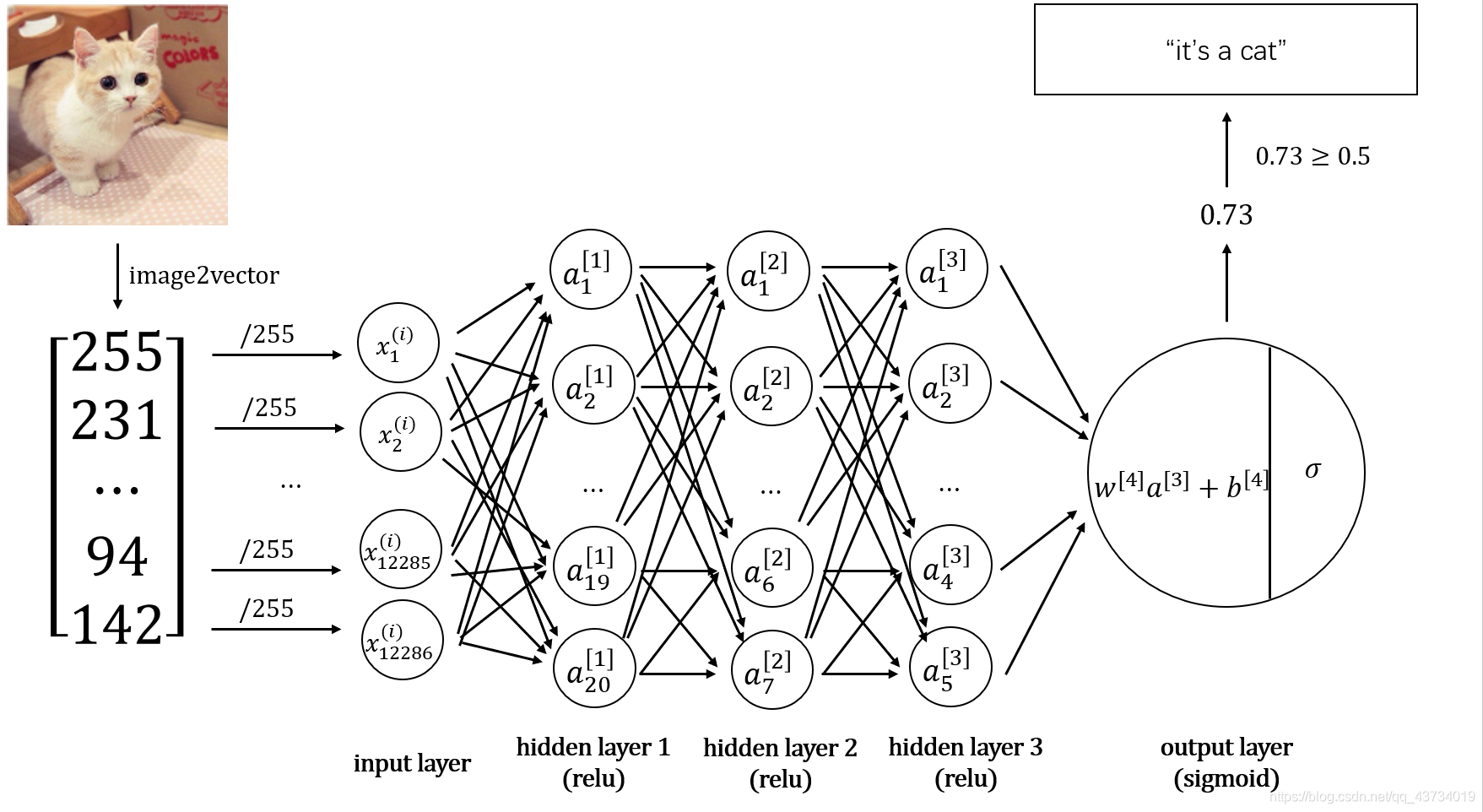
基于该神经网络模型，代码实现如下：

首先，对数据集数据进行预处理。
预处理过程与人工智能系列实验（一）完全相同。

def load_dataset():
    """
    加载数据集数据
    :return: 训练数据与测试数据的相关参数
    """
    train_dataset = h5py.File("datasets/train_catvnoncat.h5", "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:])  # 提取训练数据的特征数据，格式为(样本数, 图片宽, 图片长, 3个RGB通道)
    train_set_y_orig = np.array(train_dataset["train_set_y"][:])  # 提取训练数据的标签数据，格式为(样本数, )

    test_dataset = h5py.File("datasets/test_catvnoncat.h5", "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:])  # 提取测试数据的特征数据
    test_set_y_orig = np.array(test_dataset["test_set_y"][:])  # 提取测试数据的标签数据

    classes = np.array(test_dataset["list_classes"][:])  # 提取标签，1代表是猫，0代表不是猫

    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))  # 统一类别数组格式为(1, 样本数)
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))

    return train_set_x_orig,  train_set_y_orig, test_set_x_orig, test_set_y_orig, classes


train_set_x_orig,  train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()  # 加载数据集数据

m_train = train_set_x_orig.shape[0]  # 训练样本数
m_test = test_set_x_orig.shape[0]  # 测试样本数
num_px = test_set_x_orig.shape[1]  # 正方形图片的长/宽

train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T  # 将样本数据进行扁平化和转置，格式为(图片数据, 样本数)
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

train_set_x = train_set_x_flatten/255.  # 标准化处理，使所有值都在[0, 1]范围内
test_set_x = test_set_x_flatten/255.

其次，构造神经网络中用到的相应函数。

def sigmoid(Z):
    """
    sigmod函数实现
    :param Z: 数值或一个numpy数组
    :return: 输出A
    """
    A = 1 / (1 + np.exp(-Z))

    return A


def relu(Z):
    """
    relu函数实现
    :param Z: 数值或一个numpy数组
    :return: 输出A
    """
    A = np.maximum(0, Z)

    return A


def initialize_parameters_deep(layer_dims):
    """
    初始化各层参数w和b
    :param layer_dims: 列表，存储每层的神经元个数
    :return: 参数
    """
    parameters = {}
    L = len(layer_dims)

    # 遍历每一层
    for l in range(1, L):
        # 若该层有3个神经元，上一层有2个神经元，则该层参数W的维度是3*2，b的维度是3*1
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l - 1]) / np.sqrt(layer_dims[l - 1])
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))

    return parameters

前向传播的公式为
$$\begin{array}{c}{Z}^{[l]}=W^{[l]}{A}^{[l?1]}+b^{[l]}\\ \\ A^{[l]}=g(Z^{[l]})\end{array}$$
其中，$g$代表激活函数。

def linear_forward(A, W, b):
    """
    线性前向传播
    :param A: 上一层的输出
    :param W: 该层的参数W
    :param b: 该层的参数b
    :return: 输出Z，中间变量
    """
    Z = np.dot(W, A) + b
    cache = (A, W, b)

    return Z, cache


def linear_activation_forward(A_prev, W, b, activation):
    """
    激活线性前向传播——非线性前向传播
    :param A_prev: 上一层的输出
    :param W: 该层的参数W
    :param b: 该层的参数b
    :param activation: 字符串，激活函数类型
    :return: 输出A，中间变量
    """
    Z, linear_cache = linear_forward(A_prev, W, b)

    if activation == "sigmoid":
        A = sigmoid(Z)
    elif activation == "relu":
        A = relu(Z)

    assert (A.shape == (W.shape[0], A_prev.shape[1]))
    cache = (linear_cache, Z)

    return A, cache


def L_model_forward(X, parameters):
    """
    完整的前向传播过程
    :param X: 样本的特征数据
    :param parameters: 每一层的w和b参数
    :return: 输出AL，中间变量
    """
    caches = []
    A = X

    L = len(parameters) // 2  # 每一层有两个参数

    for l in range(1, L):
        A_prev = A
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)],
                                             activation='relu')
        caches.append(cache)

    # 最后一层前向传播
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)],
                                          activation='sigmoid')
    caches.append(cache)

    return AL, caches


def compute_cost(AL, Y):
    """
    计算成本
    :param AL: 输出层的输出
    :param Y: 样本标签数据
    :return: 成本
    """
    m = Y.shape[1]

    logprobs = np.multiply(Y, np.log(AL)) + np.multiply((1 - Y), np.log(1 - AL))
    cost = - np.sum(logprobs) / m

    assert (cost.shape == ())

    return cost

反向传播的公式为
$$\begin{array}{c}d{W}^{[l]}=\frac{1}{m}d{Z}^{[l]}{A}^{[l?1]T}\\ \\ d{b}^{[l]}=\frac{1}{m}{\sum }_{i=1}^{m}d{Z}^{[l](i)}\\ \\ d{A}^{[l?1]}=W^{[l]T}d{Z}^{[l]}\\ \\ d{Z}^{[l]}=d{A}^{[l]}?g^{\prime }(d{Z}^{[l]})\end{array}$$
其中，$g^{\prime }$代表激活函数的偏导数。

def sigmoid_backward(dA, cache):
    """
    sigmoid函数的反向传播
    :param dA: 这一层的dA
    :param cache: Z
    :return: dZ
    """
    Z = cache

    s = 1 / (1 + np.exp(-Z))
    dZ = dA * s * (1 - s)

    return dZ


def relu_backward(dA, cache):
    """
    relu函数的反向传播
    :param dA: 这一层的dA
    :param cache: Z
    :return: dZ
    """

    Z = cache
    dZ = np.array(dA, copy=True)  # dZ = dA

    dZ[Z <= 0] = 0  # z小于等于0时，dZ = 0

    return dZ


def linear_backward(dZ, cache):
    """
    线性反向传播
    :param dZ: 下一层的dZ
    :param cache: 中间变量(A, W, b)
    :return: 上一层的dA，这一层的dW，db
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = np.dot(dZ, cache[0].T) / m
    db = np.sum(dZ, axis=1, keepdims=True) / m
    dA_prev = np.dot(cache[1].T, dZ)

    return dA_prev, dW, db


def linear_activation_backward(dA, cache, activation):
    """
    激活函数的反向传播
    :param dA: 本层的dA
    :param cache: 中间变量((A, W, b), Z)
    :param activation: 字符串，激活函数类型
    :return: 上一层的dA，这一层的dW，db
    """
    linear_cache, activation_cache = cache

    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)

    dA_prev, dW, db = linear_backward(dZ, linear_cache)

    return dA_prev, dW, db


def L_model_backward(AL, Y, caches):
    """
    完整的反向传播过程
    :param AL: 输出层的输出
    :param Y: 样本标签数据
    :param caches: 中间变量，cache的列表，cache：((A, W, b), Z)
    :return: 每一层的梯度
    """
    grads = {}
    L = len(caches)
    Y = Y.reshape(AL.shape)  # 真实标签与预测标签的维度一致

    # 计算最后一层的梯度
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
    current_cache = caches[-1]
    grads['dA' + str(L - 1)], grads['dW' + str(L)], grads['db' + str(L)] = linear_activation_backward(dAL,
                                                                                                      current_cache,
                                                                                                      activation='sigmoid')

    # 计算第L-1层到第1层的梯度
    for c in reversed(range(1, L)):
        grads['dA' + str(c - 1)], grads['dW' + str(c)], grads['db' + str(c)] = linear_activation_backward(
            grads['dA' + str(c)], caches[c - 1], activation='relu')

    return grads


def update_parameters(parameters, grads, learning_rate):
    """
    利用梯度更新参数
    :param parameters: 每一层的参数
    :param grads: 每一层的梯度
    :param learning_rate: 学习率
    :return: 更新后的参数
    """
    L = len(parameters) // 2
    for l in range(1, L + 1):
        parameters['W' + str(l)] = parameters['W' + str(l)] - learning_rate * grads['dW' + str(l)]
        parameters['b' + str(l)] = parameters['b' + str(l)] - learning_rate * grads['db' + str(l)]

    return parameters

最终，组合以上函数，构建出最终的神经网络模型函数。

def dnn_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3001, print_cost=False):
    """
    完整的深度神经网络训练模型
    :param X: 样本的特征数据
    :param Y: 样本的标签数据
    :param layers_dim: 各层的神经元个数
    :param learning_rate: 学习率
    :param num_iterations: 迭代次数
    :param print_cost: 是否打印成本
    :return: 训练好的参数
    """
    costs = []

    # 初始化参数
    parameters = initialize_parameters_deep(layers_dims)

    for i in range(0, num_iterations):
        # 前向传播
        AL, caches = L_model_forward(X, parameters)
        # 计算成本
        cost = compute_cost(AL, Y)
        # 反向传播
        grads = L_model_backward(AL, Y, caches)
        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)

        # 打印成本
        if i % 100 == 0:
            if print_cost and i > 0:
                print("训练%i次后成本是：%f" % (i, cost))
            costs.append(cost)

    # 绘制成本变化曲线图
    plt.plot(np.squeeze(costs))
    plt.xlabel('iterations (per tens)')
    plt.ylabel('cost')
    plt.title('learning_rate = ' + str(learning_rate))
    plt.show()

    return parameters

现在调用上面的模型函数对我们最开始加载的数据进行训练。

layers_dims = [12288, 20, 7, 5, 1]  # 输入层有12288个神经元

parameters = dnn_model(train_set_x, train_set_y, layers_dims, num_iterations=2001, print_cost=True)

输出：训练2000次后成本是：0.1138。对训练数据的准确率为98%左右，对测试数据的准确率为80%左右。

绘制成本随训练次数变化曲线：

试验模型预测功能：

使用函数与数据均与人工智能系列实验（一）相同。这里不再赘述。

结束语：

1. 实验过程中，一定要搞清楚变量的维度，否则做数据处理、写数组操作时会容易出现问题。可以用assert函数检验数据的维度。
2. 数据集、图片等需要和代码在同一目录下。
3. 本实验与人工智能系列实验（一）均采用几乎基于纯Python的numpy库函数进行神经网络模型的搭建，目的是理解神经网络背后的数学原理及意义。我们也当然可以像实验末部分，利用sklearn库函数快速构建深度神经网络。在后续的实验中，我也会对TensorFlow等经典框架进行学习与运用。
4. 相关代码可能会不断更新改进，以github中的代码为准。
5. 神经网络层数、各层神经元个数、迭代次数、学习率等超参数需要不断尝试来找出较为合适的值，过大或过小均无法得到好的效果。
6. 在本实验中，4层的深度神经网络的效果相比于单神经元网络提高了0.1到80%，已经是一个相当大的提升幅度了。况且，由于数据规模的限制，深度神经网络的效果并没有发挥完全，随数据量的增多应会有进一步的性能提升。深度神经网络相比于单神经网络，还可以在迁移学习等各个方面发挥作用。

其余人工智能系列实验：

人工智能系列实验（一）——用于识别猫的二分类单层神经网络
人工智能系列实验（二）——用于区分不同颜色区域的浅层神经网络