[人工智能]torch.nn实现前馈神经网络（多分类）

通过torch.nn实现前馈神经网络解决多分类问题；更换三种激活函数看效果；增加隐藏层看效果；

import torch
import numpy as np
import random
from IPython import display
from matplotlib import pyplot as plt
from torch import nn
import torch.utils.data as Data
import torch.optim as optim
from torch.nn import init
import torchvision
import torchvision.transforms as transforms

#下载MNIST手写数据集
mnist_train = torchvision.datasets.MNIST(root='./Datasets/MNIST', train=True,
download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.MNIST(root='./Datasets/MNIST', train=False,
download=True, transform=transforms.ToTensor())
#读取数据
batch_size = 32
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True,
num_workers=0)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False,
num_workers=0)

#实现FlattenLayer层
class FlattenLayer(torch.nn.Module):
    def __init__(self):
         super(FlattenLayer, self).__init__()
    def forward(self, x):
        return x.view(x.shape[0],-1)

#模型定义和参数初始化
num_inputs,num_hiddens,num_outputs = 784,256,10
net = nn.Sequential(
        FlattenLayer(),
        nn.Linear(num_inputs,num_hiddens),
        nn.Sigmoid(),
        nn.Linear(num_hiddens,num_outputs)
        )

for params in net.parameters():
    init.normal_(params,mean=0,std=0.01)

#训练次数和学习率
num_epochs = 50
lr = 0.01
#定义交叉熵损失函数
loss = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(),lr)

#测试集loss
def evaluate_loss(data_iter,net):
    acc_sum,loss_sum,n = 0.0,0.0,0
    for X,y in data_iter:
        y_hat = net(X)
        acc_sum += (y_hat.argmax(dim=1)==y).sum().item()
        l = loss(y_hat,y) # l是有关小批量X和y的损失
        loss_sum += l.sum().item()*y.shape[0]
        n+=y.shape[0]
    return acc_sum/n,loss_sum/n

#定义模型训练函数
def train(net,train_iter,test_iter,loss,num_epochs,batch_size,params=None,lr=None,optimizer=None):
    train_ls = []
    test_ls = []
    for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
        train_l_sum, train_acc_num,n = 0.0,0.0,0
        # 在每一个迭代周期中，会使用训练数据集中所有样本一次
        for X, y in train_iter: # x和y分别是小批量样本的特征和标签
            y_hat = net(X)
            l = loss(y_hat, y).sum() # l是有关小批量X和y的损失
            #梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            l.backward() # 小批量的损失对模型参数求梯度
            if optimizer is None:
                SGD(params,lr)
            else:
                optimizer.step()
            #计算每个epoch的loss
            train_l_sum += l.item()*y.shape[0]
            #计算训练样本的准确率
            train_acc_num += (y_hat.argmax(dim=1)==y).sum().item()
            #每一个epoch的所有样本数
            n+= y.shape[0]
        train_ls.append(train_l_sum/n)
        test_acc,test_l = evaluate_loss(test_iter,net)
        test_ls.append(test_l)
        print('epoch %d, train_loss %.6f,test_loss %f,train_acc %.6f,test_acc %.6f'%(epoch+1, train_ls[epoch],test_ls[epoch],train_acc_num/n,test_acc))
    return train_ls,test_ls

train_loss,test_loss = train(net,train_iter,test_iter,loss,num_epochs,batch_size,net.parameters,lr,optimizer)

x = np.linspace(0,len(train_loss),len(train_loss))
plt.plot(x,train_loss,label="train_loss",linewidth=1.5)
plt.plot(x,test_loss,label="test_loss",linewidth=1.5)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.legend()
plt.show()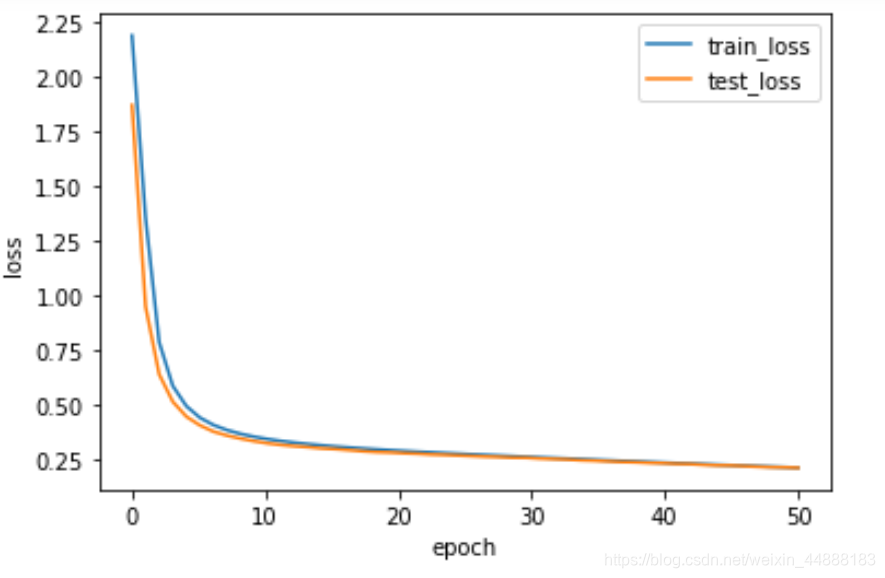

增加隐藏层和用Dropout防止过拟合：

#模型定义和参数初始化
num_inputs,num_hiddens,num_outputs = 784,256,10
net = nn.Sequential(
        FlattenLayer(),
        nn.Linear(num_inputs,num_hiddens),
        nn.ReLU(),
        nn.Dropout(0.2),
        nn.Linear(num_hiddens,num_hiddens),
        nn.ReLU(),
        nn.Dropout(0.5),
        nn.Linear(num_hiddens,num_outputs)
        )

for params in net.parameters():
    init.normal_(params,mean=0,std=0.01)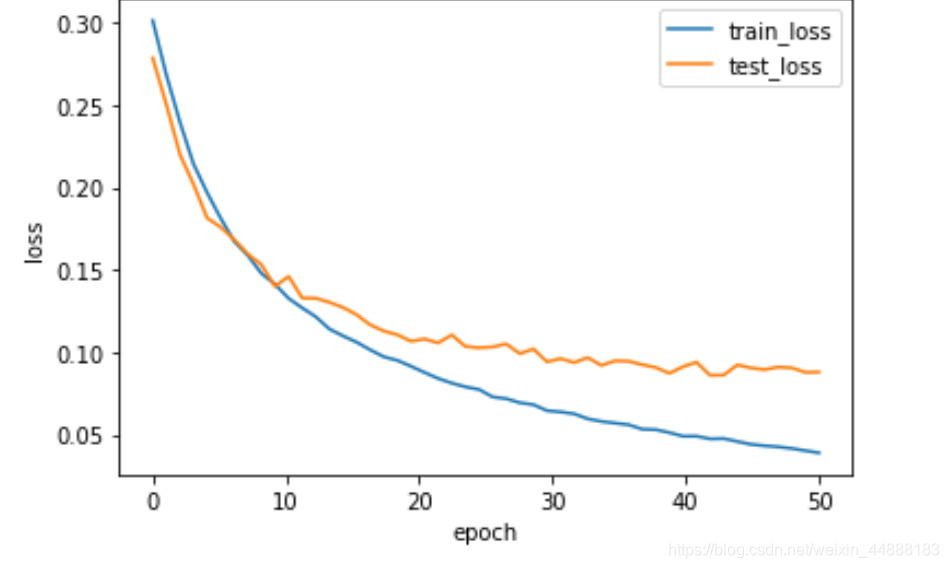

?

?