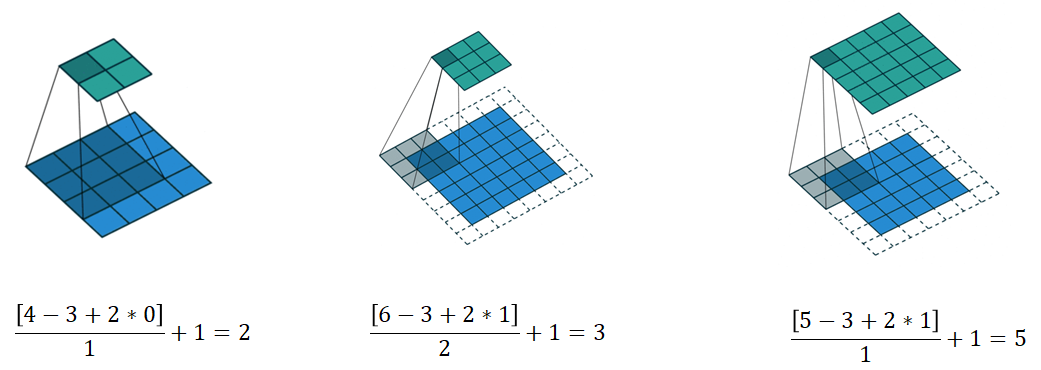
神经网络
1:感知机,可以看作单层神经网络,
输入:X1-Xn 为输入分量,W1j-Wnj为输入向量权值,theta作为阈值,f为激活函数,
输出:标量O
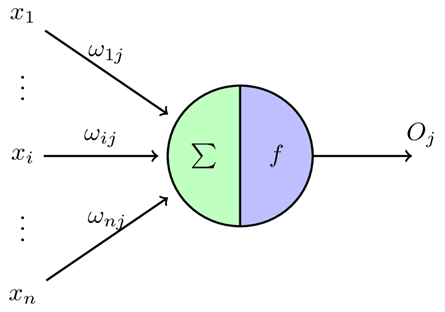
单层感知机类型一般的线性回归模型,不适合数据量大、复杂的任务
因此,构造多层感知机是必要的。
多层感知机的结构为:
1输入层------2隐藏层------3输出层
多层感知机的关键问题在于如何训练其中各层间的连接权值
↑解决该问题比较流行的方法是----反向传播BP算法
过程如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-liAMIhqc-1628602118381)(C:\Users\10305\AppData\Roaming\Typora\typora-user-images\image-20210810211044654.png)]
反向传播算法最大的功能就是让多层感知机有了训练手段(因为之前没有此只能基于 单层感知机)
卷积神经网络CNN
结构:
1:卷积层----- 提取图像特征,其卷积核权重是共享权值
2:池化层------降低特征图大小,降低后续操作量
3:全连接层----分类、输出使用
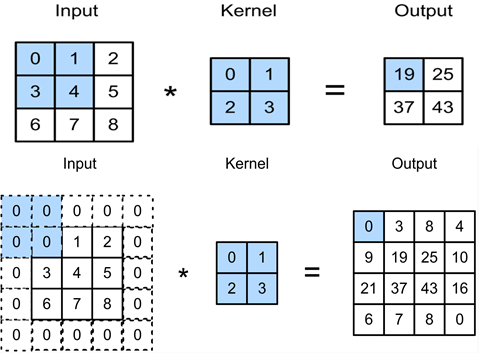
图片卷积示意图
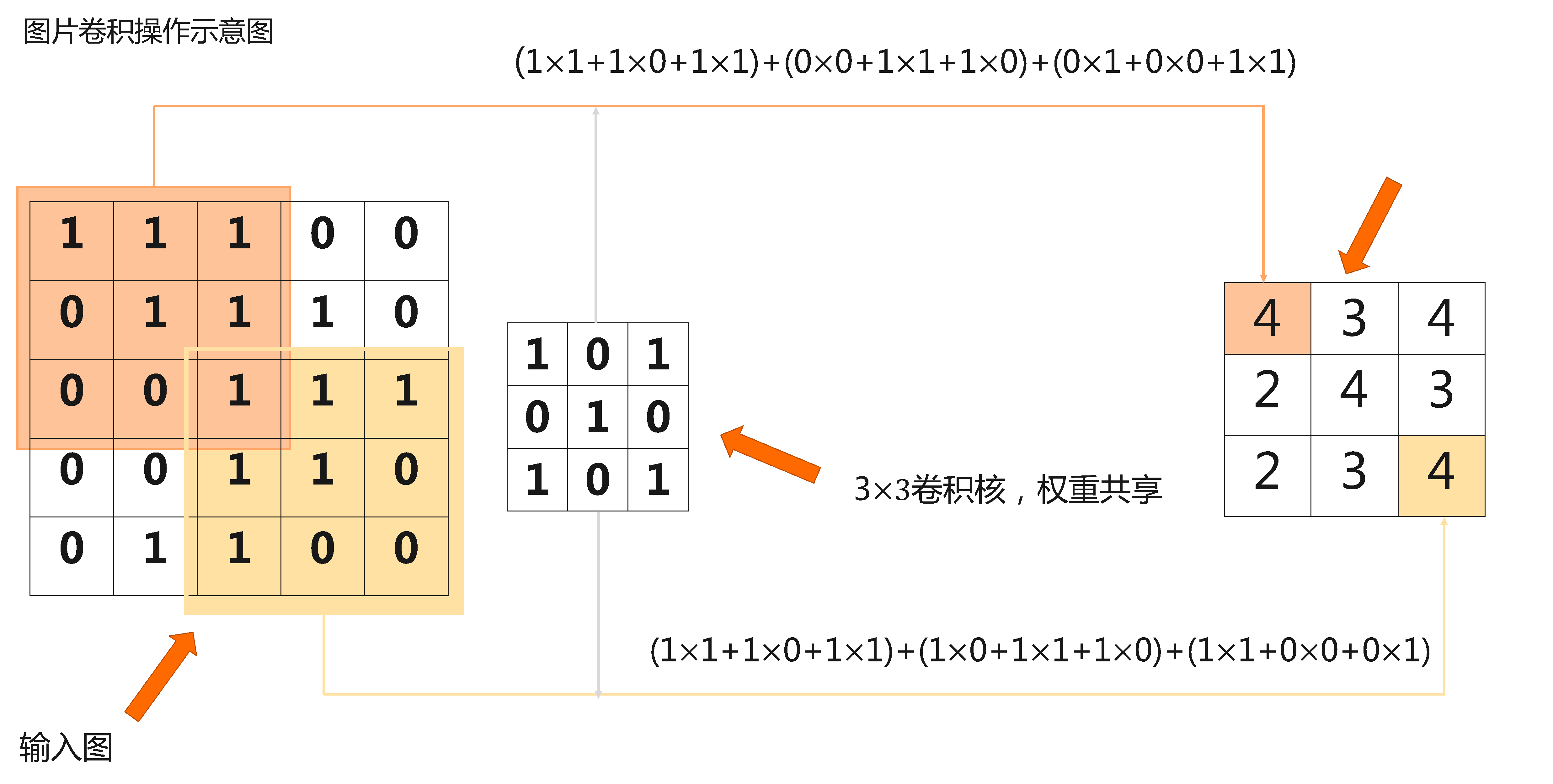
文字翻译即 左边3×3矩阵 按行依次×中间的矩阵,右下角的矩阵同理。然后得出图右的左上右下角2个数
故卷积就是:一个核矩阵在一个原始矩阵上从上往下、从左往右扫描,每次扫描都得到一个结果,将所有结果组合到一起得到一个新的结果矩阵。
代码如下
import torch
from torch import nn
def corr2d(X, K): # X 是输入,K是卷积核
h, w = K.shape # 获取卷积核的大小
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i: i + h, j: j + w] * K).sum() # 累加
return Y
X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) # 模拟一个输入
K = torch.tensor([[0, 1], [2, 3]]) # 模拟一个卷积核
corr2d(X, K)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cBI0Xirv-1628602118383)(http://tianchi-media.oss-cn-beijing.aliyuncs.com/dragonball/DL/other/img/5.1_correlation.svg)]
2:填充:目的是使卷积后图像不失真,方便计算特征图尺寸变化;弥补边界信息丢失
3:步长:卷积窗口从输入数组的最左上方开始,按从左往右、从上往下的顺序,依次在输入数组上滑动。我们将每次滑动的行数和列数称为步幅或步长
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FnszGHIb-1628602118385)(http://tianchi-media.oss-cn-beijing.aliyuncs.com/dragonball/DL/other/img/5.2_conv_stride.svg)]
该图在高上的步幅为3,在宽上的步幅为2
4:池化:作用是使特征图变小,简化网络计算复杂度;压缩特征,提取主要特征
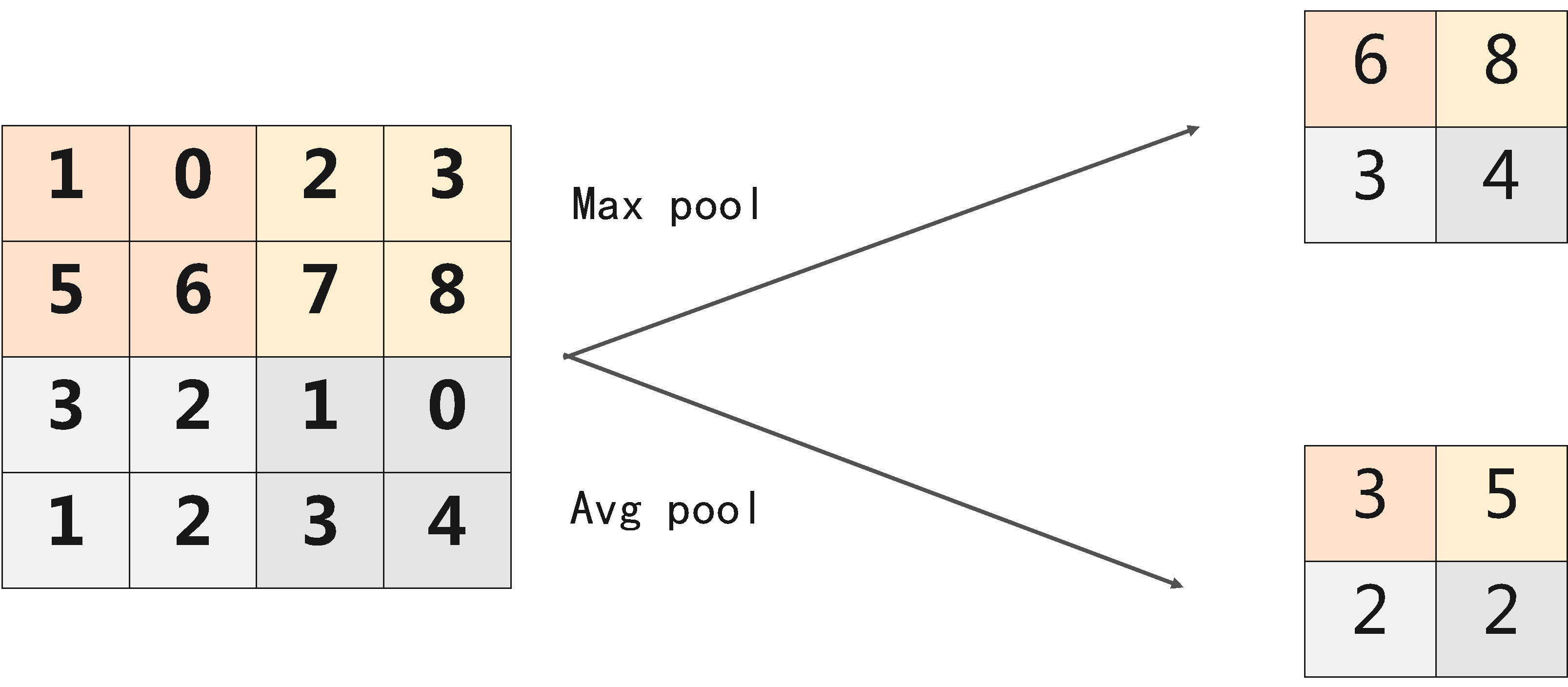
5卷积和池化输出尺寸
假设输入图片的高和宽一致,卷积核的宽和高一致,那么输入图像的尺寸与输出图像的尺寸有如下关系:
其中,FinFin 是输入图像、k 是卷积核的大小、p 是图像填充的大小、s 是卷积核的步幅、FoFo 是输出、?6.6??6.6? 是向下取整的意思,比如结果是 6.6,那么向下取整就是 6