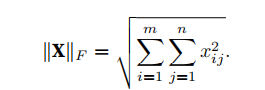线性代数
标量
标量由只有?个元素的张量表示

向量
以将向量视为标量值组成的列表。我们将这些标量值称为向量的元素(elements)或分量(components)



矩阵
向量将标量从零阶推?到?阶,矩阵将向量从?阶推?到?阶







线性代数实现
标量
标量由只有?个元素的张量表示

向量
将向量视为标量值组成的列表

可以使用下标来引用向量的任?元素
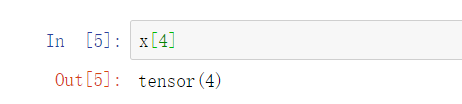
通过调用Python的内置len()函数来访问张量的长度
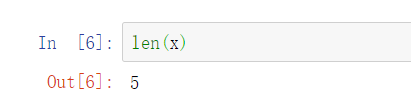
用张量表示?个向量(只有?个轴)时,可以通过.shape属性访问向量的长度

矩阵
通过指定两个分量m和 n来创建?个形状为m × n的矩阵

矩阵的转置

对称矩阵(symmetric matrix)A等于其转置:A = A?,并将B与它的转置进??较


张量
像向量是标量的推广,矩阵是向量的推广?样,我们可以构建具有更多轴的数据结构

张量算法的基本性质
给定具有相同形状的任意两个张量,任何按元素?元运算的结果都将是相同形状的张量;
注:通过分配新内存,将A的?个副本分配给B

两个矩阵的按元素乘法称为哈达玛积(Hadamard product)(数学符号⊙)

将张量乘以或加上?个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘

降维
可以对任意张量进行的?个有?的操作是计算其元素的和

可以表示任意形状张量的元素和

指定求和汇总张量的轴

指定axis=1将通过汇总所有列的元素降维(轴1)

沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和

?个与求和相关的量是平均值

计算平均值的函数也可以沿指定轴降低张量的维度

非降维求和:调用函数来计算总和或均值时保持轴数不变会很有用

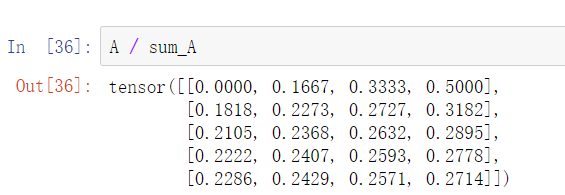
可以通过?播将A除以sum_A
沿某个轴计算A元素的累积总和,可以调?cumsum函数,此函数不会沿任何轴降低输?张量的维度。

点积
点积是相同位置的按元素乘积的和

可以通过执行按元素乘法,然后进行求和来表示两个向量的点积

矩阵-向量积
执行矩阵-向量积
注意:A的列维数(沿轴1的长度)必须与x的维数(其长度)相同

矩阵-矩阵乘法
可以将矩阵-矩阵乘法AB看作是简单地执行m次矩阵-向量积,并将结果拼接在?起,形成?个n × m矩
阵。
注:在下面的代码中,我们在A和B上执行矩阵乘法,这里的A是?个5行4列的矩阵,B是?个4行3列的矩阵。
相乘后,我们得到了?个5行3列的矩阵。

范数
假设n维向量x中的元素是x1, . . . , xn,其L2范数是向量元素平方和的平方根:


L1范数表示向量元素的绝对值之和


弗罗贝尼乌斯范数(Frobenius norm)是矩阵元素平方和的平方根