在给定一个数据集的情况下,我们如何建立起一个数学模型,以尽可能的完成对新输入数据的正确预测,这就是我们所要解决的问题,在这篇文章中,我们只讨论线性回归(当然高维模型也可以通过映射得到线性模型),数据集
被称作训练集(train?set),而我们之后用于验证模型准确性的数据就是测试集(test set)。
在上面的数据集中,我们只考虑了最简单的一种模型,即输入只有一个属性,输出标记为
。当然,其输入也有可能是一个向量如
,而我们要建立的线性模型,就可以用函数表示如下:
其中的就是我们要计算的模型的参数。为了方便下文表示及方便理解,定义如下:
好了,清楚了我们这个模型的大体架构之后,下一步就是对模型参数进行求取了,但是这么多参数,我们如何找出最优秀的一组解呢,这就引出了损失函数(Loss Function)的概念,损失函数的作用就是对我们的模型进行一个评估,其函数值越小代表模型在训练集上越优秀。对于上述模型,我们定义损失函数如下
当然,上述损失函数是对于只有一个属性时的表述,对于我们提到的多维输入变量
,其损失函数可以写作下面这种形式:
得到了损失函数,我们怎么找到令他最小的那一组参数呢,方法很简单,求导,求导的过程西瓜书上并没给,所以我在这里简单的说一下。
求导过程不要试图先将函数转化为一堆参数值的形式,应充分利用求导的加法原理,先拆解成几个矩阵再进行求导,这样一来计算过程就会简便很多。
? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
拆分成如下四个矩阵后,我们发现和
是一个1*1的矩阵且其值相等,因此可将其转化成一个矩阵,接下来的工作就是令其分别对
求导,这一部分所涉及到的数学公式再次就不再证明了。
令其等于0即可求得解,当然,要注意是否是一个可逆矩阵,若可逆,则最终求得结果为
那么除了求导,还有什么简单的方法么,毕竟对于每一个损失函数都去矩阵求导,其工作量也是不小的,有没有什么方法能让计算机帮我们进行这些计算呢,因此,下面我们将要介绍梯度下降算法来解决这个问题。
梯度下降算法,是用来寻找局部最小值的算法,你可以想象为自己的下山过程,每走一步前都会寻找最陡峭的方向,以期更快的达到想要的解。该算法并不保证求出来的一定是全局最小值。这个时候,我们不再把损失函数看成一堆矩阵的乘法,而是将其看作有着很多参数的函数方程,分别对于这些参数进行求导,以得到下一步该往那个方向走,进而更新模型参数。除此之外,还有一个参数叫做学习率(learning rate),你可以将其理解为通常说的步长,若是步长过大,很容易越过最优解,从而达不到我们要的效果,若是步长过小,那么算法就需要执行很多时间,效率就比较低,因此如何找到一个合适的步长也是十分重要的,在后文我们也会聊一下如何选择合适的步长。
接下来我们就以模型为例来说一下梯度下降算法。
首先可以看到,该模型模型共有两个参数,所以一开始我们要给其设定一个初值
,此外,为方便描述,我们不妨将学习率设为定值
,同之前的思想一样,我们要找的参数要使得损失函数足够小,在本例中,损失函数为:
我们对其参数分别求取偏导数,得到结果如下
偏导数为正呢,就说明参数与函数值正相关,因此参数应该减小,反之则该增大,因此参数的更新过程如下:
算法什么时候可以停止呢,一般来说有两种情况,第一种是设置一个迭代次数,在多少次后自动停止,第二种则是比较两次迭代过程的差异,若是差异值小于某个阈值,就认为已经找到了比较好的解,算法结束。
最基本的梯度下降算法大致就是这样,接下来我们再以更加细节的方法讲一下。
首先,在模型未知的情况下,如何选择构成模型的数据也是一个比较困难的问题,比如说对于一个输入样例具有n种属性的情况,哪些属性可能影响最终的结果呢,更为甚者,这两者之间是否是线性关系也是不确定的。对于模型较为简单的情况,我们可能发现模型的误差会比较大,而对于模型较为复杂的情况,我们又可能出现过拟合(overfitting)的问题,即模型在训练集表现很好但是在测试集则不尽如人意。
对于这个问题,我认为或许可以通过协方差来说明各属性之间的联系,协方差是对于两个变量之间关联程度的一种刻画,两个变量之间的协方差定义如下
这样我们就可以选出和我们将要预测的值关系较大的属性了,其次就是过拟合的问题,过拟合一般可以通过增加数据量或者添加正则项的方法来解决。
对于增加数据量的方法,其实一般只适用于一些特殊问题,比如图像识别,你可以将图片翻转之后作为一个新的输入,以此来增加样本量,而添加正则项则是比较通用的一种方法,其思想是改变损失函数,使模型尽可能的简单,以符合奥卡姆剃刀定理。举个简单的例子,修改后的损失函数可以是如下形式:
说完了大致模型,就是对于数据的预处理了,之所以会有对于数据的预处理过程,就是为了防止某个属性因其值过大而抵消了很重要但值比较小的属性的作用,处理方法一般是将原有数据改成相应的0-1正态分布。这种方法叫做feature scaling,其处理方式如下,其中代表属性数据的均值,
代表属性数据的标准差:
然后再来说一下学习率,学习率一般和每个参数以及迭代次数有关,一开始可能比较大,随着迭代次数的增长越来越小,比如说一种常用的学习率的计算方法就是这样的
但是这种方法只解决了步长的问题,可能并不能适应所有参数的特点。这里就引出了AdaGrad算法,AdaGrad算法每个参数的学习率都把它除上之前微分的均方根。
公式我不想打了,贴图吧,注意那个就是我们前边说的学习率
,因此该表达式是可以化简的
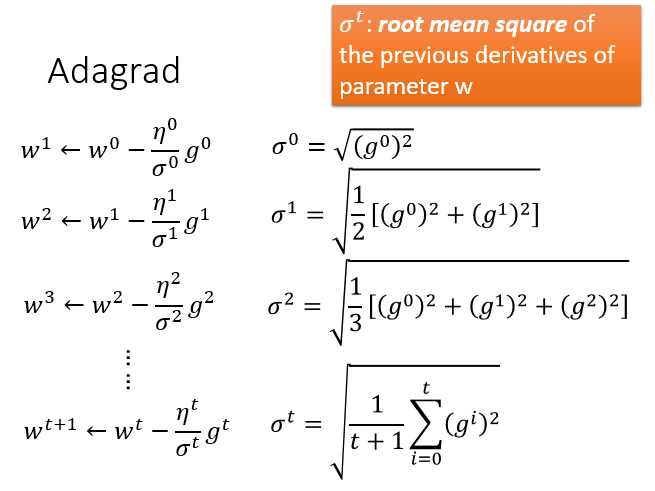
?李宏毅老师还提出了一个疑问点,即梯度下降算法中,梯度越大,说明步伐越大,但Adagrad分母里梯度越大,又说明步伐越小,这里不是会有矛盾吗?
从直观的角度解释,这种方法突出的就是当前梯度与之前梯度的反差,我们对于分子分母同除当前梯度可以看出,若当前梯度比之前的梯度大好多,那么这次其学习率也比较大,反之,其学习率也就会比较小。
从数学角度来考虑,最优的学习率应该同一次偏导成正比,二次偏导成反比,而AdaGrad则是利用一次偏导来近似二次偏导(说真的这部分我没看懂所以建议去看下视频)
此外,还有一种随机梯度下降(stochastic Gradient Descent)方法,他同梯度下降算法的区别是每一次随机取一个sample,然后损失函数改为只考虑这一个sample的误差,据此来计算梯度更新参数。这样一来,我们减轻了计算的难度,并且可能更快的计算出结果。
尽管我并不知道这样是否能够计算出正确的结果,算法是否可靠,但是我现在也不想看了,就贴张图算了。
?第一章就差不多这些内容,下一章有空看分类之类的,还有就是论文阅读,我这周还没看也得看了好累啊==