1.传统RNN的缺点和lstm的提出

以图像识别为例，图像识别存在退化问题。退化:当网络隐藏层变多时，网络的准确度达到饱和然后急剧退化，而且这个退化不是由过拟合引起的。
神经网络隐藏层数过多后效果变差，重要因素是出现梯度消失或爆炸，即反向链式传播累乘导致参数过大或过小。梯度消失:神经网络累乘引发的参数过小问题，对于任意x，其求导后的梯度可能为w1 x w2 x w3…wn，当w1、w2、w3…wn都在0-1之间时，此时w1 x w2 x w3…wn趋近于0，网络基本不再更新。梯度爆炸:神经网络累乘引发的参数过大问题，对于任意x，其求导后的梯度可能为w1 x w2 x w3…wn，当w1、w2、w3…wn都大于1时，此时w1 x w2 x w3…wn趋近于无穷大，参数值溢出，网络基本不可用。
对于退化，ResNet提出了残差网络解决这个问题。残差网络的残差单元以跳层连接的形式实现，将单元的输入直接与单元输出加在一起。该网络在ImageNet和CIFAR-10等图像任务上取得了非常好的结果。
至于跳层连接为什么会有这么好的效果，我们举两个例子进行形象理解:
1、照片回忆
现在有一张大头照，我们看到照片后进行回忆，然后描述该人的样貌。第一次回忆描述，因为比较仓促，我们不能很好的说出该人的具体特点；第二次回忆描述，我们对该人的样貌有了更具体的提炼，能描述出该人是不是在笑、发型怎么样；第三次回忆，我们又有了更清晰的描述，能描述出这个人的痣在哪、眼睛大小；第四次回忆，我们的记忆开始模糊；到第n次的时候，我们已经完全记不清这个人长什么样了。
我们得出结论，给出一张照片，回忆三次效果最佳。我们总共要回忆n次照片，怎么样保持效果最佳?很简单，在倒数第三次(对应n-3的位置)，我们再看一次照片即可。即我们将原始信息一直保存，在需要该信息时再取出查看，达到最佳的效果。
2、语言描述
某一语句“I grew up in France.I speak fluent ____.” ，让我们猜测下划线内容，我们可以很容易写出"French"，即"我在法国长大，我讲法语"的翻译。但是句子变长时，比如增长为“I grew up in France.One of the appeals of RNNs is the idea that they might be able to connect previous information to the present task, such as using previous video frames might inform the understanding of the present frame. If RNNs could do this, they’d be extremely useful. I speak fluent ____.”，让我们再对下划线内容进行猜测，就很不容易了。因为我们在阅读过程中，慢慢的把一开始的内容忘记了。这时如果我们再想要回答这个问题，在我们阅读的时候，可以把"France"这个单词圈住，形成长期记忆。即阅读的同时做重点，在后期答题时直接看这些圈住的重点。
从上方两个例子可以看出，我们想要更有效的提取信息，直接将原始信息向后传，在需要的时候拿出来使用，在不使用时几乎保持不变即可。而残差网络与lstm正是这样做的，两者有异曲同工之妙。

2.lstm的结构

2.1总体结构差异

传统RNN网络结构:
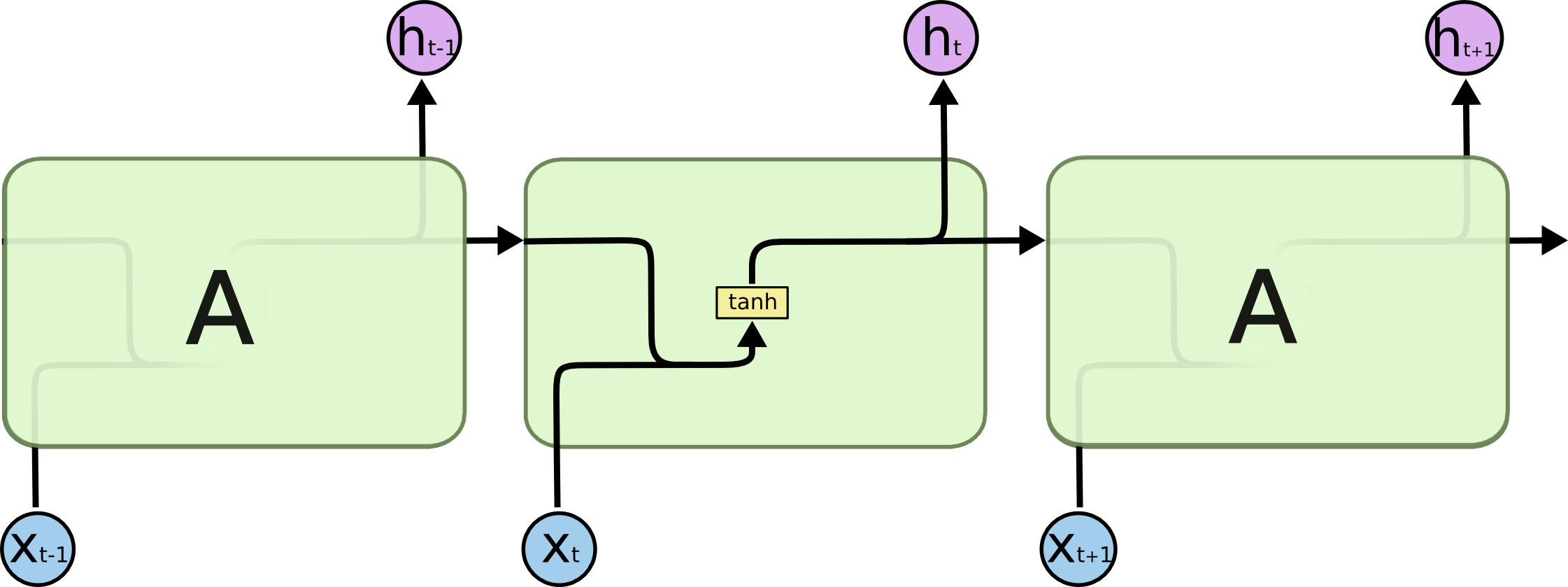
在这里插入图片描述
与传统RNN网络结构相比，lstm增加了一个长时间记忆的C:

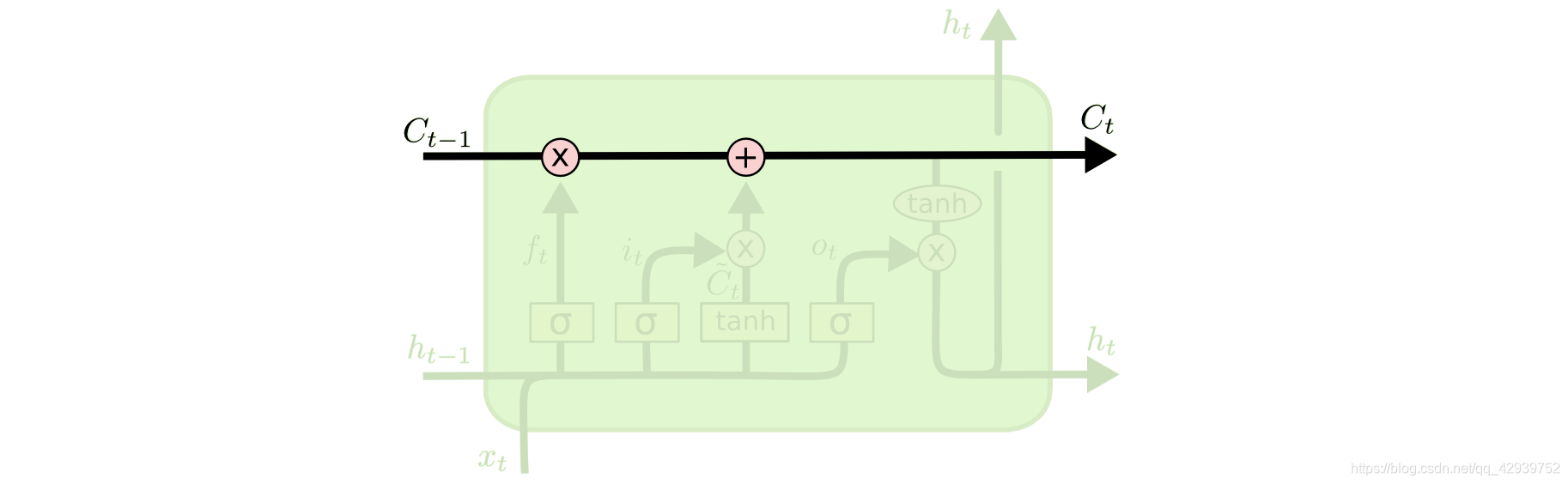
C由上一层的输出和本层的输入共同决定，同时本层的输入和上一层的输出又影响下一层的结果，所以总体结构如下:

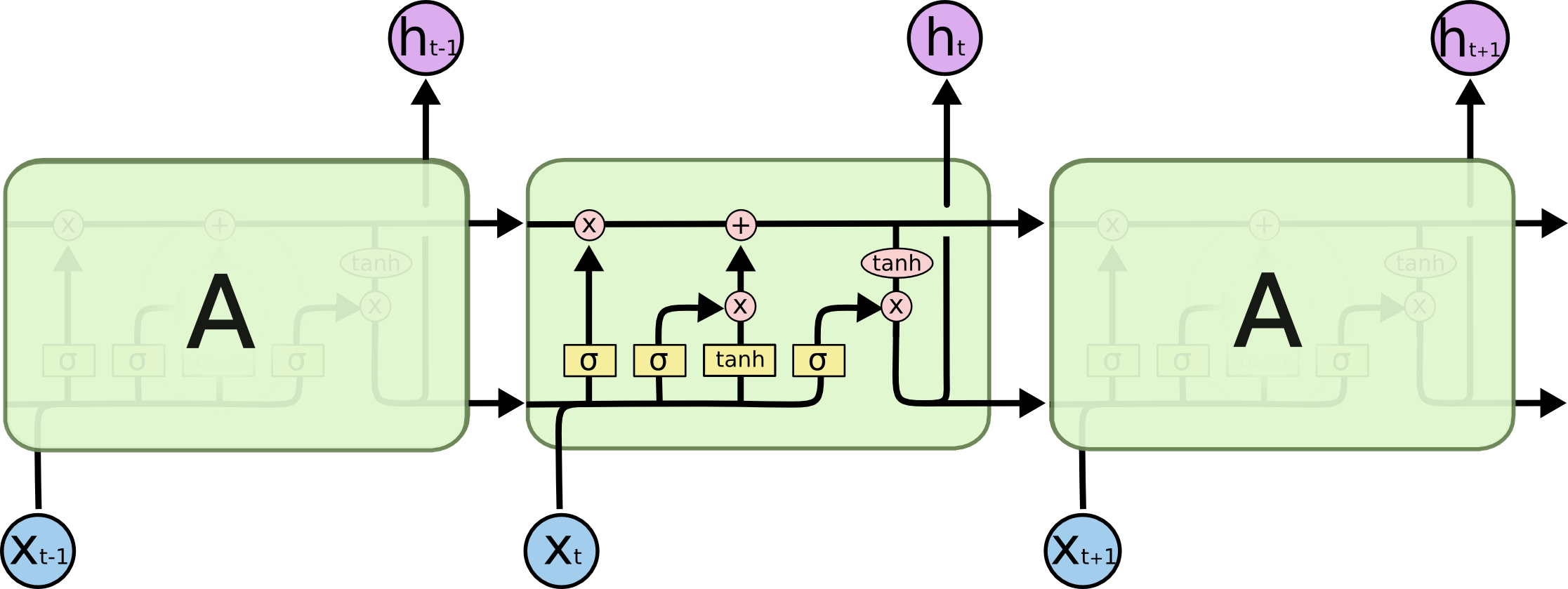
2.2遗忘门

遗忘门部分结构图与计算公式如下图所示。 ${{\rm{W}}_f} \cdot [{h_{t - 1}},{x_t}]$ 是n:1的神经网络(n输入，1输出)，此输出加上偏置 ${b_f}$ 形成 ${{\rm{W}}_f} \cdot [{h_{t - 1}},{x_t}] + {b_f}$ ，最后由sigmoid将其放缩到0-1。即总公式为 ${\rm{sigmoid(}}{{\rm{W}}_f} \cdot [{h_{t - 1}},{x_t}] + {b_f})$ ，下图右方公式为其简化表示。
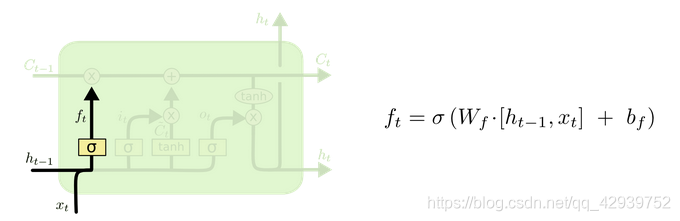
在这里插入图片描述
${f_t}$ 的作用在于决定保存多少上一层的数据信息。上一层输入为 ${C_{t - 1}}$ ，上一层的信息保留部分 ${C_t} = {f_t} \cdot {C_{t - 1}}$ ，若 ${f_t}$ =0(此时 ${C_t}$ =0)，网络将遗忘上一层的所有的信息； ${f_t}$ =1( ${C_t} = {C_{t - 1}}$ )，网络将保存上一层的所有的信息； ${f_t}$ 处于0-1之间，则遗忘部分信息。
为了形象理解遗忘门的作用，我们以“I grew up in France.I speak fluent ____.”（预测下划线单词，答案为"French"）为例:
（1）首先我们输入"I"的词向量，此时 ${C_{t - 1}}$ =0， ${f_t}$ 的值不造成任何影响。
（2）接下来我们输入"grew"的词向量，“I”这个词对最后产生"French"影响不大(我们假设"French"只与句子中的“France”相关联），我们尽可能使 ${f_t}$ 趋近于0，减少无关信息对最终结果造成影响。
（3）我们输入"up"的词向量，“I grew”短句对最后产生"French"影响不大，我们尽可能使 ${f_t}$ 趋近于0。
（4）我们依次输入“in”和“France”，所要做的操作基本相同，使 ${f_t}$ 趋近于0。
（5）当我们输入“I”的词向量时， ${C_{t - 1}}$ 已经包含“France”的信息(上个输入词为“France”），此时我们要尽可能使 ${f_t}$ 趋近于1，将“France”的信息保存下来。
（6）当我们输入“speak”时， ${C_{t - 1}}$ 已经包含“France”的信息，我们尽可能使 ${f_t}$ 趋近于1，将“France”的信息保存下来。
（7）对“fluent ”也是如此操作，最终通过保存的信息成功预测出"French"。
由上述例子我们可以得知，遗忘门的作用在于决定保存上一层信息量的多寡。

2.3输入门

输入门的部分结构图与计算公式如下图所示。输入门的作用在于决定是否保存本次输入的数据信息，保留多少。
${{\rm{W}}_C} \cdot [{h_{t - 1}},{x_t}]$ 是n: $l e n (C)$ 的神经网络(n输入， $l e n (C)$ 输出， $l e n (C)$ 指数据信息量C的长度)，本层提取的数据信息为: ${\tilde C_t} = \tanh ({{\rm{W}}_C} \cdot [{h_{t - 1}},{x_t}] + {b_C})$ 。
${{\rm{W}}_i} \cdot [{h_{t - 1}},{x_t}]$ 是n:1的神经网络(n输入，1输出)，对应本层应保存的信息量多寡: ${i_t}$ = ${\rm{sigmoid(}}{{\rm{W}}_i} \cdot [{h_{t - 1}},{x_t}] + {b_f})$ 。
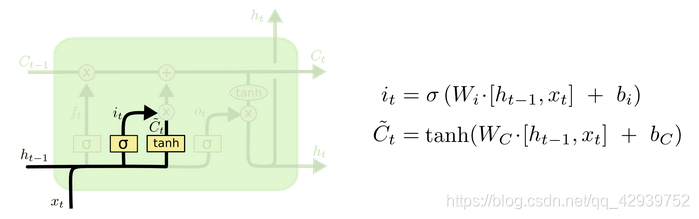
在这里插入图片描述
${\tilde C_t}$ 是本层提取的数据信息， ${i_t}$ 的作用在于决定保存多少本层的数据信息。本层输出为 ${\tilde C_t} = {i_t} \cdot {\tilde C_t}$ ，若 ${i_t}$ =0(此时 ${\tilde C_t}$ =0)，网络将不保存本层提取的数据信息； ${i_t}$ =1( ${\tilde C_t}$ = ${\tilde C_t}$ )，网络将保存本层提取的所有的信息； ${i_t}$ 处于0-1之间，则遗忘部分信息。
为了形象理解输入门的作用，我们仍以“I grew up in France.I speak fluent ____.”（预测下划线单词，答案为"French"）为例:
（1）首先我们输入"I"的词向量，“I”这个词对最后产生"French"不造成影响，此时令 ${i_t}$ 趋近于0，则 ${\tilde C_t}$ 趋近于0，不保存我们提取出来的"I"的信息。
（2）接下来我们输入"grew"的词向量，“grew”这个词对最后产生"French"影响不大，我们尽可能使 ${i_t}$ 趋近于0，减少无关信息对最终结果造成影响。
（3）我们依次输入"up"和“in”的词向量，影响仍不大，我们尽可能使 ${i_t}$ 趋近于0，不保存本层提取的信息。
（4）当我们输入“France”的词向量时，因为"French"由“France”的信息推测得来，我们要尽可能的保存“France”的信息，即尽可能使 ${i_t}$ 趋近于1（ ${\tilde C_t} \simeq {\tilde C_t}$ ），将“France”的信息保存下来。
（5）我们依次输入"I"和“speak ”的词向量，影响仍不大，我们尽可能使 ${i_t}$ 趋近于0，不保存本层提取的信息。
（6）对“fluent ”也是如此操作，最终通过保存的“France”信息成功预测出"French"。
由上述例子我们可以得知，输入门的作用在于决定保存本层信息量的多寡。

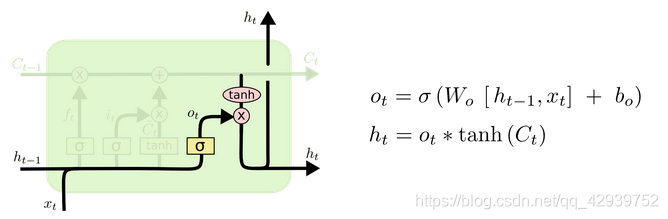
2.4输出门

输出门的部分结构图与计算公式如下图所示。输出门产生隐藏量 ${{\rm{h}}_t}$ ， ${{\rm{h}}_t}$ 与下一层神经元的提取信息方式相关联。
${W_o}[{h_{t - 1}},{x_t}]$ 是n:1的深度神经网络(n输入，1输出)， ${o_t} =sigmoid ({W_o}[{h_{t - 1}},{x_t}] + {b_o})$ 是0到1之间的浮点数，决定 ${C_t}$ 输出量的多寡。 ${h_t} = {o_t} \cdot \tanh ({C_t})$ 为最终输出量。
在这里插入图片描述
${C_t}$ 是本层最终的数据信息， ${o_t}$ 的作用在于决定本层对下一层的作用以及输出信息量。本层输出为 ${h_t} = {o_t} \cdot \tanh ({C_t})$ ，若 ${o_t}$ =0(此时 ${h_t}$ =0)，网络输出为0，本层网络保存的信息对下一层网络不造成影响； ${o_t}$ =1( ${h_t} = \tanh ({C_t})$ )，网络将保存 ${C_t}$ 的所有信息； ${o_t}$ 处于0-1之间，则遗忘部分信息。
我们以“I grew up in France, I’ve been to Germany, my hometown is ____.”（预测下划线单词，答案为"France"）为例:
“come from”、“France”、“hometown”共同决定答案"France"，当输入为“France”时， ${h_t}$ 应包含“come from”的信息，此时 ${o_t}$ 是一个接近1的数（接近程度由“come from”和“France”的亲密程度决定）；输入"Germany"，前文几乎不造成影响，也无法得到有效信息，此时可令 ${o_t}$ 趋近于0；遇到“hometown”时，预测输出与之相关，则又令 ${o_t}$ 接近于1，最终得到正确输出"France"。
由上述例子我们可以得知，输出门的作用在于产生包含层间联系信息的隐藏量 ${h_t}$ 。

3.代码演示

我们以N vs 1结构为例进行代码编写。
任务:预测句子中下划线的值
句子:

(1)“I come from China,I speak fluent __”,
(2)“I grew up in Germany,I speak fluent __”

(3)“I have been to France,I speak fluent__”

下划线真实值分别为"Chinese",“German”,“French”。
步骤如下
(1)首先制作输入句子和标签的词典:

sentences=[["I","come","from","China","I","speak","fluent"],\
          ["I","grew","up","in","Germany","I","speak","fluent"],\
          ["I","have","been","to","France","I","speak","fluent"]]
target_language=["Chinese","German","French"]
sentence_total=[]
for sentence in sentences:
    sentence_total+=sentence
words_dict={x:i for i,x in enumerate(set(sentence_total))}#输入句子的词字典
words_dict_flip={i: x for x,i in words_dict.items()}#输入句子的词翻转字典
target_num={x:i for i,x in enumerate(target_language)}#目标输出的字典
target_num_flip={i: x for x,i in target_num.items()}#目标输出的翻转字典

生成的词典为：

words_dict={'come': 0, 'grew': 1, 'have': 2, 'Germany': 3,'in': 4,'fluent': 5,'from': 6,'up': 7,'France': 8, 'speak': 9, 'I': 10,'been': 11,'China': 12,'to': 13}
words_dict_flip={0: 'come',1: 'grew',2: 'have',3: 'Germany',4: 'in',5: 'fluent',6: 'from',7: 'up',8: 'France',9: 'speak',10: 'I',11: 'been',12: 'China',13: 'to'}
target_num={'Chinese': 0, 'German': 1, 'French': 2}
target_num_flip={0: 'Chinese', 1: 'German', 2: 'French'}

(2)接下来，我们Embedding生成数据集（voc_size为输入句子无重复词汇个数；embedding_size为Embedding后的词向量长度，这里我们设置为3）:

#产生数据单元
def make_data(sentences,target_language,words_dict,target_num,voc_size,embedding_size):
    embedding = nn.Embedding(len(words_dict), 3, sparse=True)
    inputs=[]
    labels=[]
    i=0
    for sentence in sentences:
        sentence_vector=[]
        for word in sentence:
            sentence_vector.append(embedding(torch.tensor(words_dict[word])))
        inputs.append(sentence_vector)
        labels.append(target_num[target_language[i]])
        i+=1
    return inputs,Variable(torch.LongTensor(labels))

生成的输入数据inputs如下:
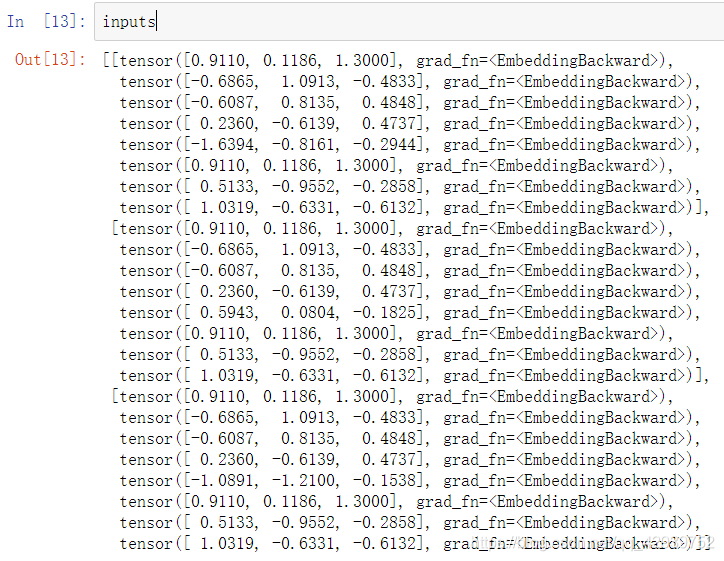
在这里插入图片描述
生成的labels标签:

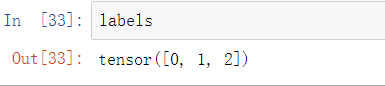
(3)制作完数据集，我们开始搭建lstm神经网络。这里按照前边的计算公式即可，与传统RNN的差异在于我们不仅要输出output和hidden，还要输出c值。
神经网络代码如下：

class LSTM(nn.Module):
    #模型初始化
    def __init__(self,hidden_size,embedding_size,output_size):
        super(LSTM,self).__init__()
        #遗忘门
        self.generate_f=nn.Linear(hidden_size+embedding_size, 1)
        self.sigmoid_forget_gate=nn.Sigmoid()
        #输入门
        self.input_gate_layer=nn.Linear(hidden_size+embedding_size, hidden_size)
        self.generate_i=nn.Linear(hidden_size+embedding_size, 1)
        self.tanh_input_gate=nn.Tanh()
        self.sigmoid_input_gate=nn.Sigmoid()
        #输出门
        self.generate_o=nn.Linear(hidden_size+embedding_size, 1)
        self.tanh_output_gate=nn.Tanh()
        self.sigmoid_output_gate=nn.Sigmoid()
        #最终输出
        self.out=nn.Linear(hidden_size, output_size)
        self.softmax = nn.Softmax(dim=-1)
    #前向传播层
    def forward(self,inputs,hidden,c):
        middle=torch.cat((inputs,hidden),-1)#拼接输入词和hidden
        #遗忘门计算
        f=self.sigmoid_forget_gate(self.generate_f(middle))
        c=c*f
        #输入门计算
        i=self.sigmoid_input_gate(self.generate_i(middle))
        c_input=self.tanh_input_gate(self.input_gate_layer(middle))
        c=c+i*c_input
        #输出门计算
        o=self.sigmoid_output_gate(self.generate_o(middle))
        hidden=o*self.tanh_output_gate(c)
        #分类输出
        output=self.softmax(self.out(hidden))
        return output,hidden,c

(4)我们开始编写训练模型的代码。此处和传统RNN的差别在于，我们每次要多输入一个c值，且每次输入一个新句子，我们都要重新初始化hidden和c为0。

#设置600个epoch训练模型
for epoch in range(600):
    for i,sentence_voc in enumerate(inputs):#sentence_voc:某一句子的全部词向量
        hidden=hidden0#每个句子的起始hidden值设置为0
        c=c0#每个句子的起始c值设置为0
        for word_vector in sentence_voc:#word_vector:句子的某一词向量
            output,hidden,c=lstm(word_vector,hidden,c)
        optimizer.zero_grad()
        loss = criterion(output.unsqueeze(0), labels[i].unsqueeze(0))
        loss.backward(retain_graph=True)
        optimizer.step()

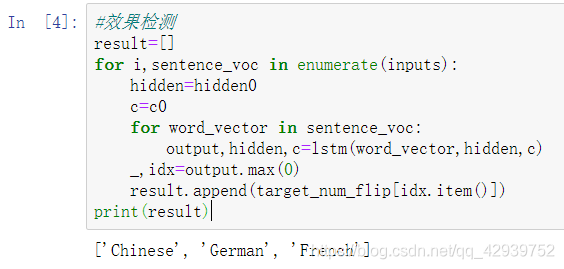
(5)最后进行效果检测，如下图所示，输出与真实值完全一致，说明已经成功预测。值得一提的是尽管我们这里输入数据集和测试集相统一，我仍然训练了接近600个回合才达到过拟合的程度。在传统RNN模型中的另外一个任务中，我训练了30个回合就达到已经过拟合。尽管任务不同，但是也可以初步体现出lstm相比于rnn需要消耗更多计算资源的特点，当然lstm效果也比传统rnn效果好得多。
在这里插入图片描述
完整代码：

import torch.nn as nn
import torch
import jieba
import torch.optim as optim#优化器
from torch.autograd import Variable
class LSTM(nn.Module):
    #模型初始化
    def __init__(self,hidden_size,embedding_size,output_size):
        super(LSTM,self).__init__()
        #遗忘门
        self.generate_f=nn.Linear(hidden_size+embedding_size, 1)
        self.sigmoid_forget_gate=nn.Sigmoid()
        #输入门
        self.input_gate_layer=nn.Linear(hidden_size+embedding_size, hidden_size)
        self.generate_i=nn.Linear(hidden_size+embedding_size, 1)
        self.tanh_input_gate=nn.Tanh()
        self.sigmoid_input_gate=nn.Sigmoid()
        #输出门
        self.generate_o=nn.Linear(hidden_size+embedding_size, 1)
        self.tanh_output_gate=nn.Tanh()
        self.sigmoid_output_gate=nn.Sigmoid()
        #最终输出
        self.out=nn.Linear(hidden_size, output_size)
        self.softmax = nn.Softmax(dim=-1)
    #前向传播层
    def forward(self,inputs,hidden,c):
        middle=torch.cat((inputs,hidden),-1)#拼接输入词和hidden
        #遗忘门计算
        f=self.sigmoid_forget_gate(self.generate_f(middle))
        c=c*f
        #输入门计算
        i=self.sigmoid_input_gate(self.generate_i(middle))
        c_input=self.tanh_input_gate(self.input_gate_layer(middle))
        c=c+i*c_input
        #输出门计算
        o=self.sigmoid_output_gate(self.generate_o(middle))
        hidden=o*self.tanh_output_gate(c)
        #分类输出
        output=self.softmax(self.out(hidden))
        return output,hidden,c
#产生数据单元
def make_data(sentences,target_language,words_dict,target_num,voc_size,embedding_size):
    embedding = nn.Embedding(len(words_dict), 3, sparse=True)
    inputs=[]
    labels=[]
    i=0
    for sentence in sentences:
        sentence_vector=[]
        for word in sentence:
            sentence_vector.append(embedding(torch.tensor(words_dict[word])))
        inputs.append(sentence_vector)
        labels.append(target_num[target_language[i]])
        i+=1
    return inputs,Variable(torch.LongTensor(labels))
if __name__=="__main__":
    sentences=[["I","come","from","China","I","speak","fluent"],\
          ["I","grew","up","in","Germany","I","speak","fluent"],\
          ["I","have","been","to","France","I","speak","fluent"]]
    target_language=["Chinese","German","French"]
    sentence_total=[]
    for sentence in sentences:
        sentence_total+=sentence
    words_dict={x:i for i,x in enumerate(set(sentence_total))}#输入句子的词字典
    words_dict_flip={i: x for x,i in words_dict.items()}#输入句子的词翻转字典
    target_num={x:i for i,x in enumerate(target_language)}#目标输出的字典
    target_num_flip={i: x for x,i in target_num.items()}#目标输出的翻转字典
    voc_size=len(words_dict)#原始文本去重单词个数
    embedding_size=3#embedding后的词向量长度
    inputs,labels=make_data(sentences,target_language,words_dict,target_num,voc_size,embedding_size)#产生数据
    hidden_size=3#模型中hadden的长度
    hidden0=torch.zeros(hidden_size)
    c0=torch.zeros(hidden_size)#c全零初始化，一开始不包含任何数据信息
    output_size=len(set(target_num))#语言数量
    criterion = nn.CrossEntropyLoss()#使用交叉熵
    lstm=LSTM(hidden_size,embedding_size,output_size)
    optimizer = optim.Adam(lstm.parameters(),lr=0.001)#使用Adam优化算法更新参数
    #设置600个epoch训练模型
    for epoch in range(1000):
        for i,sentence_voc in enumerate(inputs):#sentence_voc:某一句子的全部词向量
            hidden=hidden0#每个句子的起始hidden值设置为0
            c=c0#每个句子的起始c值设置为0
            for word_vector in sentence_voc:#word_vector:句子的某一词向量
                output,hidden,c=lstm(word_vector,hidden,c)
            optimizer.zero_grad()
            loss = criterion(output.unsqueeze(0), labels[i].unsqueeze(0))
            loss.backward(retain_graph=True)
            optimizer.step()
    #效果检测
    result=[]
    for i,sentence_voc in enumerate(inputs):
        hidden=hidden0
        c=c0
        for word_vector in sentence_voc:
            output,hidden,c=lstm(word_vector,hidden,c)
        _,idx=output.max(0)
        result.append(target_num_flip[idx.item()])
    print(result)