[人工智能]Lukarov‘s 假期学习笔记（三）

机器学习模型评估方法

1. 留出法

留出法将dataset划分成两个互斥的集合，一个做训练集，另一个做测试集。在划分训练/测试集的时候要保证数据分布的一致性，需要根据数据中的类别比例来分层采样与随机采样。常见做法时将大约2/3~4/5的样本用于训练，其余用于测试。

2. 交叉验证法（cross validation）

交叉验证法先将数据集D划分为k个大小相近的互斥子集，每个子集尽可能保持数据分布的一致性，即通过分层采样得到；然后用k-1个子集的并集作训练集，余下一个做测试集，共进行k次训练与测试，最终返回k次训练结果的均值。
交叉验证法又称“k折交叉验证”，k常取10。
交叉验证法在样本数据少的情况下有一个特例，叫留一法。

3. 自助法（bootstrapping）

自助法以自助采样（bootstrap sampling）为基础。
给定包含m个样本的数据集$D$，我们对它进行采产生数据集$D^{\prime }$：每次随机从$D$中挑选一个样本，将其拷贝到$D^{\prime }$，然后再将该样本放回初始数据集$D$中，使得该样本在下次采样时仍可能被采到；执行m次之后，就得到了包含m个样本的数据集$D^{\prime }$，并将其作为训练集，$D?D^{\prime }$用作测试集。
自助法在数据集较小、难以划分训练/测试集时很有用，能从初始数据集中产生多个不同的训练集，对集成学习等方法有很大的好处。

机器学习模型性能度量

给定数据集 D = { ( x 1 , y 1 ) , . . . , ( x m , y m ) } D=\left \{ (x_{1},y_{1}),...,(x_{m},y_{m}) \right \} D={(x1?,y1?),...,(xm?,ym?)}，对学习器$f$进行性能评估。

回归任务最常用的性能指标是 “均方误差”（mean squared error, MSE)

$E(f;D)=\frac{1}{m}{\sum }_{i=1}^m(f(x_i)?y_i{)}^2$

下面是分类任务常用的性能指标

1. 错误率与精度

错误率是分类错误的样本数占样本总数的比例，精度是分类正确的样本数占样本总数的比例。

2. 查准率（precision）、查全率（recall）与F1

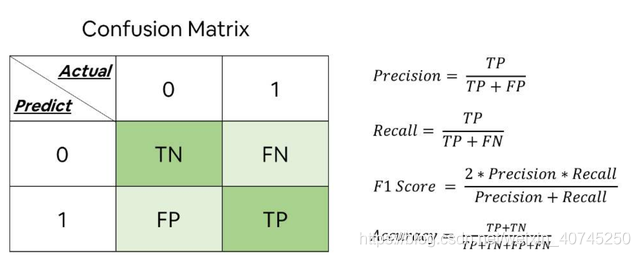
对二分类问题，可将样例根据其真实类别和学习器预测类别的组合划分为真正例(true positive)、假正例(false positive)、真反例(true negative)和假反例(false negative)四种情形，显然有TP + FP + TN + FN = 样本总数。分类结果的“混淆矩阵”如下表所示，显然查准率和查全率的数值成反比。

P-R曲线 即查准率-查全率曲线，以查准率为纵轴、查全率为横轴作图，可以通过P-R曲线下面积来比较学习器的优劣，但实际的P-R曲线是非单调、不平滑的，不好积分，所以用“平衡点”（Break-Even Point，简称BEP）即“查准率等于查全率”时的取值来判断，更常用的是F1度量。
*F1*是基于查准率和查全率的调和平均定义的：$\frac{1}{F1}=\frac{1}{2}?(\frac{1}{P}+\frac{1}{R})$
即$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{样例总数+TP?TN}$
根据实际情况下对查全率和查准率的偏重程度，$F1$度量又有一般形式——$F_{\beta }$：
$F_{\beta }=\frac{(1+{\beta }^2)\times P\times R}{({\beta }^2\times P)+R}$，其中$\beta$=1时退化为标准的F1，$\beta$>1时查全率影响更大，$\beta$<1时查准率影响更大