[人工智能]“智能”（3）——激活函数&三节点神经网络

一、激活函数

1. 为什们要用激活函数

由于前四节课我们所用的模型都是基于理论上用线性的模型去描述一个系统，但是现实生活中大多数问题是分类问题。我么们只需要直到他究竟是好是坏，并不需要知道他好的比例是多少坏的比例是多少。所以我们使用$logistic$函数机器学习中叫$sigmoid$函数曲线来拟合我们所需要的预测曲线。

sigmoid函数如下图

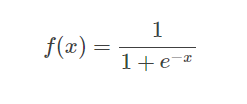
图形曲线

具体详细请参考：链接: Sigmoid函数.

2、为什么不用阶跃函数，而是用sigmoid函数？

阶跃函数能够很完整的区别好和坏这个分类但是由于阶跃函数的求导是一个冲激函数（两边零阶跃处无穷）而sigmoid函数的导数在一段区间内都是有数值的更加便于我们进行梯度下降。故而使用sigmoid函数而不是阶跃函数
阶跃函数：

冲激函数：

二、样例分析

import dataset
import matplotlib.pyplot as plt
import numpy as np

xs,ys = dataset.get_beans(100)

plt.title("size-toxicity function" , fontsize = 12 )
plt.xlabel("been size")
plt.ylabel("toxicity")
plt.scatter(xs,ys)

# "随机梯度下降"
for _ in range(10000):				#进行了10000次的迭代学习
    for i in range(100):
        x = xs[i]
        y = ys[i]

        z = w*x+b
        a = 1/(1 + np.exp(-z))
        e = (y-a)**2
        
        deda = -2*(y-a)
        dadz = a*(1-a)
        dzdw = x

        dedw = deda*dadz*dzdw
        dzdb = 1
        dedb = deda*dadz*dzdb
        alpha = 0.05
        w = w - alpha*dedw
        b = b - alpha*dedb

    if _%200 == 0:						#每学习200次更新一下图像，可以让图像更加快速更新完成
        plt.clf()
        plt.scatter(xs,ys)
        z = w * xs + b
        a = 1/(1 + np.exp(-z))

        plt.xlim(0,1)
        plt.ylim(0,1.5)
        plt.plot(xs, a)
        plt.pause(0.001)

分析：
现在我们的模型变成了
$a=1/(1+exp(?z))$（z = w * xs + b）
代价函数变成了：
$e=(y?a{)}^2$

所以我们要预测的最优量就有$w,b$但是要求$w,b$就要求函数e上a的偏导才能通过求导的链式法则，进而求出$w,b$的偏导注：求偏导的作用是用于反向传播调整修正力度的大小。

三、隐藏层——三个节点的神经网络

红色圆圈表示的就是每次反向传播所需要更新的数据，每个数据都需要进行求偏导，得出来的偏导进行梯度下降进而找到最优的曲线。

以上是B站ele实验室 上课学习笔记。