[人工智能]【MindSpore深度学习框架】实现简单线性回归

一.生成数据集

1.自定义数据集生成函数

我们首先定义了一个函数，是用来进行生成数据的，我们生成的数据是带有噪音的，$y=x?w+b+noise$ ，我们可以看到下图就是我们生成的数据以及拟出的直线。

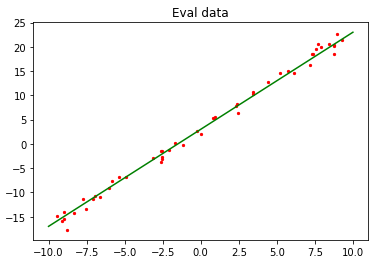
这里我们为什么要用yield返回呢？是因为我们为了提高效率，并不一次性返回所有数据，而是采用迭代器形式返回单一数据。

def get_data(num,w=2,b=3):
    for data in range(num):
        x=np.random.uniform(-10,10)
        noise=np.random.normal(0,1)
        y=x*w+b+noise
        yield np.array([x]).astype(np.float32),np.array([y]).astype(np.float32)

通过我们的生成函数，我们生成5个数据进行展示

eval_data=list(get_data(5))
x_eval_label,y_eval_label=zip(*eval_data)

eval_data

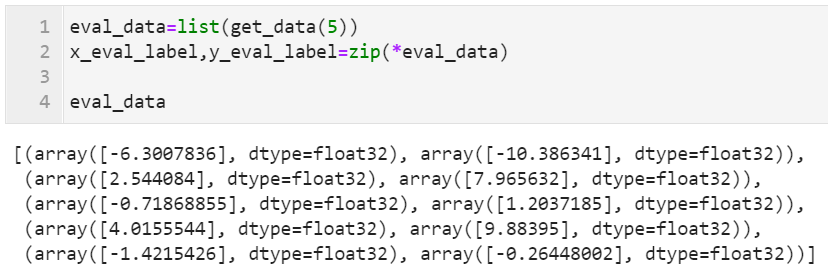
2.定义数据增强函数

下面定义个函数进行生成数据，我们一般叫增强函数，为什么呢？是因为我们使用这个函数读取数据后，之后一般要将其进行一系列的处理，比如更换通道、调整图片大小等，我们这里只是单纯数值数据，所以没有使用那么多的处理，只是使用了数据分批，和数据重复。

• batch：代表将原始数据进行分批，即没批数据的数量
• repeat：代表将数据重复多少次，因为有些时候样本数据不足，需要进行扩充

from mindspore import dataset as ds

def create_dataset(num_data,batch_size=16,repeat_size=1):
    input_data=ds.GeneratorDataset(list(get_data(num_data)),column_names=['data','label'])
    input_data=input_data.batch(batch_size) # 设置数据批次
    input_data=input_data.repeat(repeat_size) # 设置数据重复次数
    return input_data

这里我没准备生成1600个测试数据，16个数据为一个批次，重复数据1次

data_number=1600
batch_number=16
repeat_number=1

ds_train=create_dataset(data_number,batch_number,repeat_number)
print('数据集批次：',ds_train.get_dataset_size())
dict_datasets=next(ds_train.create_dict_iterator())

print(dict_datasets.keys())
print('X:',dict_datasets['data'].shape)
print('y:',dict_datasets['label'].shape)

数据集批次： 100
dict_keys(['data', 'label'])
X: (16, 1)
y: (16, 1)

二、定义神经网络

我们使用最简单的线性函数模型：
$$f(x)=wx+b$$
我们定义任何网络块时，要将此类继承nn.Cell类，来实现一些模块的基本功能，在__init__中进行定义网络层的基本信息，在construct中定义传播过程。

from mindspore import nn
from mindspore.common.initializer import Normal

class LinearNet(nn.Cell):
    def __init__(self):
        super(LinearNet,self).__init__()
        # 定义一个线形层，同时初始化权重和偏置
        self.fc=nn.Dense(1,1,Normal(0.02),Normal(0.02),has_bias=True) 
    
    def construct(self,x):
        x=self.fc(x)
        return x

这里我们打印下模型的参数：

net=LinearNet()
model_params=net.trainable_params()
for param in model_params:
    print(param,param.asnumpy())
    
Parameter (name=fc.weight, shape=(1, 1), dtype=Float32, requires_grad=True) [[-0.02366124]]
Parameter (name=fc.bias, shape=(1,), dtype=Float32, requires_grad=True) [0.00739245]

三、定义传播网络

1.前向传播

我们要将我们之前定义的网络进行实例化，来达到前向传播过程。

net=LinearNet()

2.损失函数

我们需要使用一种评估指标来进行评估我们模型评估的好坏，这里因为是回归，所以我们用的是MSE均方误差，损失函数如下：
$$J(w)=\frac{1}{2m}\sum _{i=1}^m(h(x_i)?y^{(i)}{)}^2$$
假设训练数据第i个数据为(xi,y(i))，公式中的参数解释如下：

• J(w)为损失值
• m为样本数据的数量，本例中m的值为batch_number
• h(xi)为第ii个数据的xixi值代入模型网络后的预测值
• y(i)为第ii个数据中的y(i)值（label值）

net_loss=nn.loss.MSELoss()

3.反向传播

反向传播网络的目标就是要不断的进行更新其权重，来达到拟合我们的样本数据，从而使得我们的loss达到最小值，所以使用梯度下降的方式进行更新其权重：
$$w_{t+1}=w_t?\lambda \frac{?J(w_t)}{?w}$$

• wt为迭代后的权重值

• wt?1为迭代前的权重值
• α为学习率
• ?J(wt?1 )?w为损失函数对权重wt的导数

# 这里优化器的参数传入的为我们模型的训练参数，以及学习率等
opt=nn.Momentum(net.trainable_params(),learning_rate=0.005,momentum=0.9)

4.前向传播与反向传播关联

定义完成前向传播和反向传播后，在MindSpore中需要调用Model函数，将前面定义的网络，损失函数，优化器函数关联起来，使之变成完整的计算网络。

from mindspore import Model
model=Model(net,net_loss,opt)

四、拟合可视化

1.可视化函数

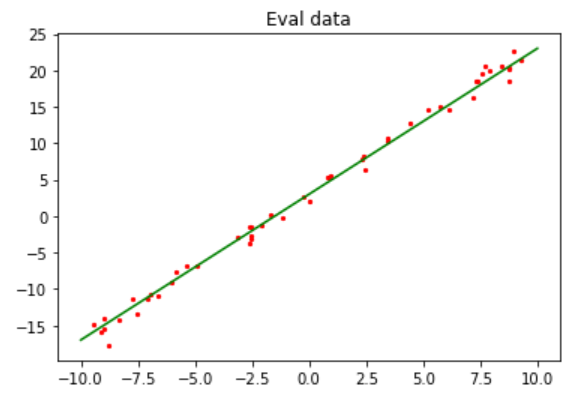
由于我们的模型需要多次迭代，所以需要定义个函数进行画出我们此时模型拟合的直线以及真实的数据拟合直线做对比

import matplotlib.pyplot as plt
from mindspore import Tensor
import time

def plot_model_and_datasets(net, eval_data):
    weight = net.trainable_params()[0]
    bias = net.trainable_params()[1]
    x = np.arange(-10, 10, 0.1)
    y = x * Tensor(weight).asnumpy()[0][0] + Tensor(bias).asnumpy()[0]
    x1, y1 = zip(*eval_data)
    x_target = x
    y_target = x_target * 2 + 3

    plt.axis([-11, 11, -20, 25])
    plt.scatter(x1, y1, color="red", s=5)
    plt.plot(x, y, color="blue")
    plt.plot(x_target, y_target, color="green")
    plt.show()

2.回调函数

MindSpore为我们提供了工具，可以进行自定义回调函数，可以实时的控制模型的训练过程，这里我们将上述定义的画图函数传入，可以在训练的过程中实时画出模型拟合的曲线。

from IPython import display
from mindspore.train.callback import Callback

class ImageShowCallback(Callback):
    def __init__(self, net, eval_data):
        self.net = net
        self.eval_data = eval_data

    def step_end(self, run_context):
        plot_model_and_datasets(self.net, self.eval_data)
        # 清除打印内容，实现动态拟合效果
        display.clear_output(wait=True)

五、执行训练

完成以上过程后，可以使用训练数ds_train对模型训练，这里调用model.train进行，其中参数解释：

• epoch：训练迭代的整个数据集的次数。
• ds_train：训练数据集。
• callbacks：训练过程中需要调用的回调函数。
• dataset_sink_model：数据集下沉模式，支持Ascend、GPU计算平台，本例为CPU计算平台设置为False。

from mindspore.train.callback import LossMonitor

epoch = 1
imageshow_cb = ImageShowCallback(net, eval_data)
model.train(epoch, ds_train, callbacks=[imageshow_cb], dataset_sink_mode=False)

plot_model_and_datasets(net, eval_data)
for net_param in net.trainable_params():
    print(net_param, net_param.asnumpy())

其实这里的图是不断进行刷新的，由于不可以演示视频，所以截了几张图片进行模拟，由于上面训练过程制定了回调函数所以是可以进行在模型训练过程中实时观看到每个时刻模型拟合的直线。

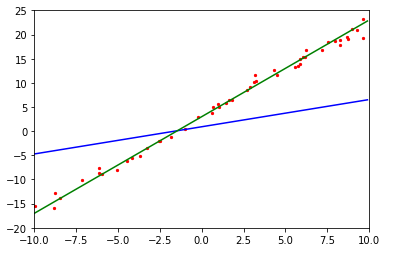
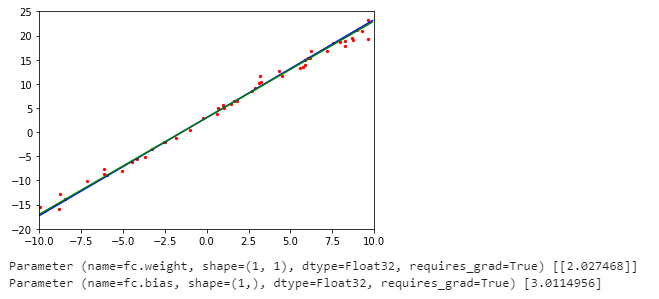
最终我们训练的权重为2.0274468，偏置为3.0114956，我们最初设定的为2和3，所以可以看到我们模拟的效果较为不错。

写在最后

? ????????大家好，我是阿光，觉得文章还不错的话，记得“一键三连”哦！！！

关注博主即可阅读全文