Intriguing properties of neural networks（ICLR2014）

这篇文章被认为是对抗样本的开山之作，首次发现并提出了对抗样本，作者阵容豪华，被引了很多次。但是文章的名字是《神经网络有趣的特性》，着重理解一下作者笔下神经网络的特性，特别是作者对对抗样本的解释，之后还有其他角度解释的文章。

对抗样本

文章通过求解以下优化问题找到对抗样本：
$\text { Minimize } c|r|+\operatorname{loss}_{f}(x+r, l) \text { subject to } x+r \in[0,1]^{m}$
其中 $c$ 是控制 $∣ r ∣$ 的大小， $r$ 对样本 $x$ 加的扰动， $loss_f$ 是神经网络对应的损失函数， $l$ 是错误分类的标签，即 $\neq l$ 。用L-BFGS来求解该优化问题。

文章发现：

所选的网络（MNIST、QuocNet、AlexNet），对于每个样本都能生成非常接近、视觉上难以区分的对抗样本。
对抗样本具有跨模型的泛化能力：在A模型上产生的对抗样本，有很大一部分在B模型（和A模型结构相同，超参数不同）上也有效（也能是B模型错误分类）
在D1数据集训练得到的模型上产生的对抗样本，在D2数据集训练得到的模型上也有效，D1和D2属于不同的子集，两个模型是结构完全不同的模型

神经网络有趣的特性

第一个特性：包含语义信息的不是单个神经元，而是整个神经元激活的空间里

关于神经网络的语义分析，之前的工作认为：神经网络的语义信息独立地保存在每一个神经元内，特别是在最后一个隐藏层中，每一个神经元都可以作为数据的一个语义特征 (semantic feature)。以上观点可以用如下式子表述：
$x^{\prime}=\underset{x \in \mathcal{I}}{\arg \max }\left\langle\phi(x), e_{i}\right\rangle$
这里的 $\in \mathcal{I}$ 是未经训练的图像集， $\phi(x)$ 是模型某一层的输出， $e_i$ 对应该层natural basis vector : $e_{i}=(0, \ldots, 1, \ldots 0)$ 。这样选出的 $x^{'}$ 应该是包含同一种（相似的）语义信息，即神经元 $e_i$ 所包含的信息。实验结果如下图：

但是，如果我们随机选一个natural basis vector $v$ ，我们用同样的计算方法选出一批 $x^{'}$ ：
$x^{\prime}=\underset{x \in \mathcal{I}}{\arg \max }\langle\phi(x), v\rangle$
这样的随机生成的 $v$ 不单独代表任意一个神经元，按理说包含的语义信息应该不会高度一致啊。实验结果如下图所示：

然而发现随机 $v$ 选出的样本，也具有相似的语义特征。

因此语义信息是存在于该隐层划分的整个空间中，而不是单个神经元。

第二个特性：DNN的输入-输出映射在很大程度不是连续的

对于传统方法，给定图像细微的扰动通常不会改变类比判定，但是对于深层神经网络，许多核方法背后的平滑假设不成立。正是因此，可以通过对网络的输入加微弱的扰动，来得到相差很多的输出，即对抗样本。

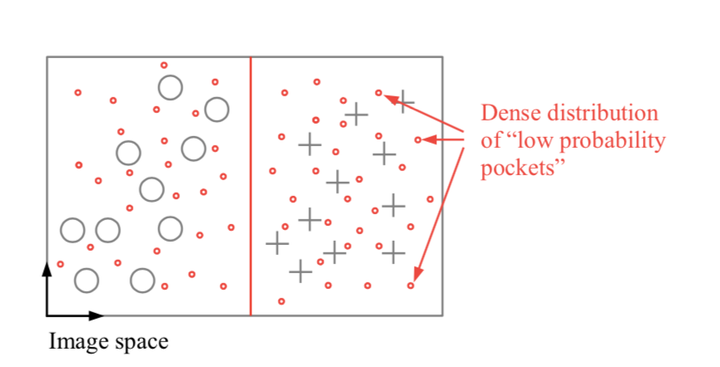
对抗样本的解释——Low-probability “pockets” in the manifold

作者认为对抗样本表示的是流形中的低概率(高维)“口袋”，仅通过围绕给定样本随机的对输入进行变换采样很难有效的找到这些口袋（例如输入图像变换）。

这个意思大概和分类边界不确定有些相似。训练集只能覆盖一部分数据分布，对于模型没有见过的数据，如果它不存在于训练集的数据分布中，那模型很有可能是分不出来的。

作者提到了可以用有理数的稠密性来理解：

假如我们需要一个分类器 $C$ ：能够区分正实数和负实数。由于在整个实数集中，无理数的个数比有理数多很多很多，那么我们收集数据的时候，收集到的数大部分都是无理数，我们用这些无理数来训练分类器，用这些无理数来测试，发现正确率很高。可实际上，我们训练出来的分类器 $C$ 是个区分正负无理数的分类器，并非是区分正负实数的分类器。

由于，有理数是稠密的，即给定一个无理数 $X$ ，总有一个有理数 $X^{'}$ 无限接近这个无理数，那么当我们用 $X^{'}$ 放到分类器 $C$ 测试，极有可能就分不出现正负。