[人工智能]李宏毅机器学习（19）

Unsupervised Learning - Linear Methods

无监督学习可以分为两类：

• 化繁为简（聚类 Clustering，降维 Dimension Reduction）：输入各种各样的树，输出一个简化抽象的树
• 无中生有（Generation）：输出对应的代码，输出各种各样的树

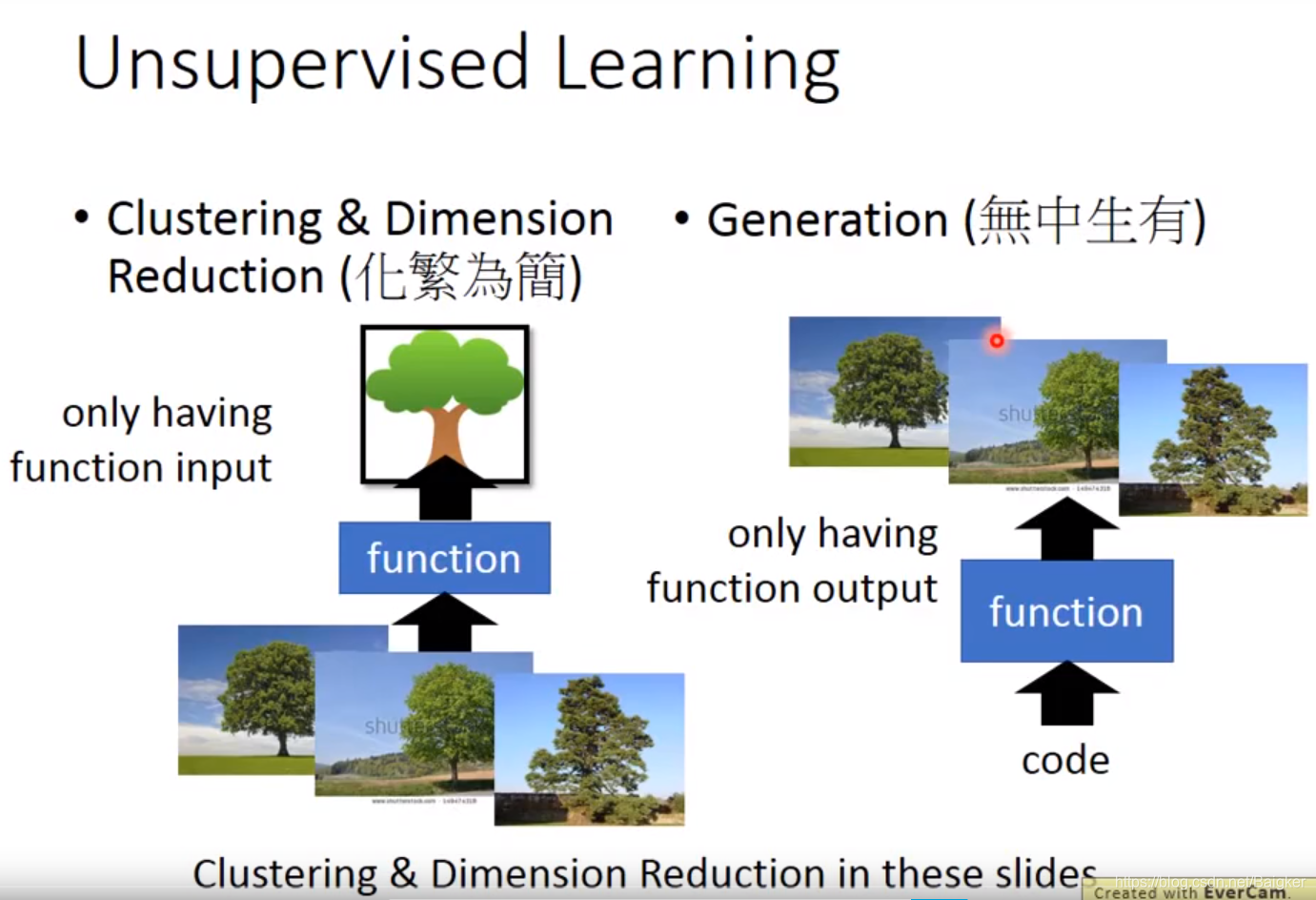
Clustering（聚类）

就是把各个无标签的数据进行分类。手动打上cluster 1、cluster 2、cluster 3的标签，这个分类过程就是化繁为简的过程。
那么，分成几类呢？有一种K-means的方法：
注：如果不是从原先的data set里取center的初始值，可能会导致部分cluster没有样本点

还有一种HAC的方法：

1. 每次选择两个相似度最高的点，合成一个点。直到合成一个root。
2. 选取阈值（threshold），形象来说就是在构造好的tree上横着切一刀，相连的叶结点属于同一个cluster
   
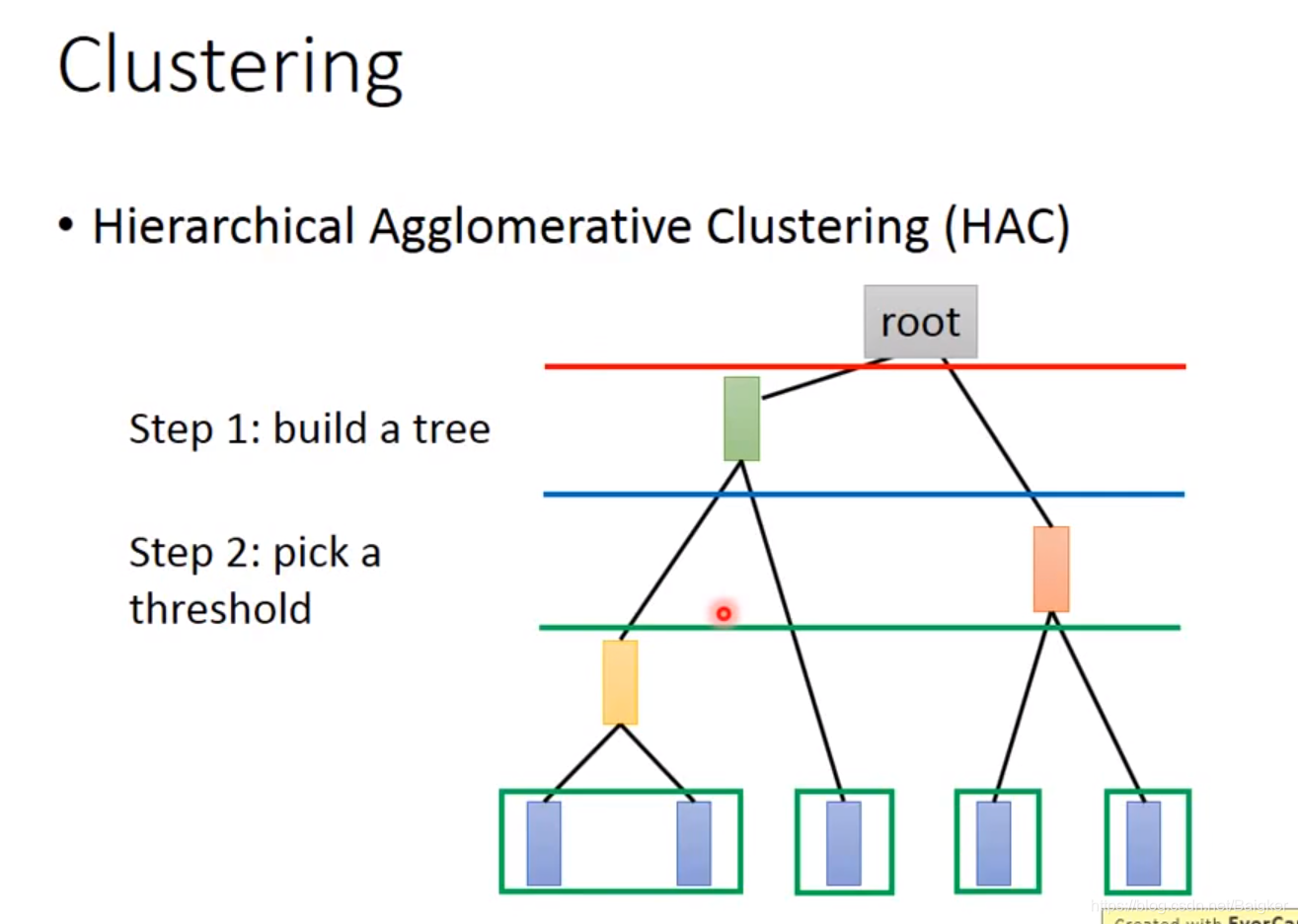
   HAC和K-means最大的区别在于如何决定cluster的数量，在K-means里，K的值是要你直接决定的；而在HAC里，你并不需要直接决定分多少cluster，而是去决定这一刀切在树的哪里。

Dimension Reduction

但是，聚类的方法有一个最大的问题：很多东西并不能直接说属于哪一类，他可能同时具有多个类的属性。
比如：一个人可以会多国语言，因此并不能把他定义为“xx语言者”。
因此，我们应该用一个向量来表示一个物体。
这就叫Distributed Representation。
如果原先的object是high dimension的，比如image，那现在用它的属性来描述自身，就可以使之从高维空间转变为低维空间，这就是所谓的降维(Dimension Reduction)

举例而言，有的图片实际上只需要很少的维度就能表示了：

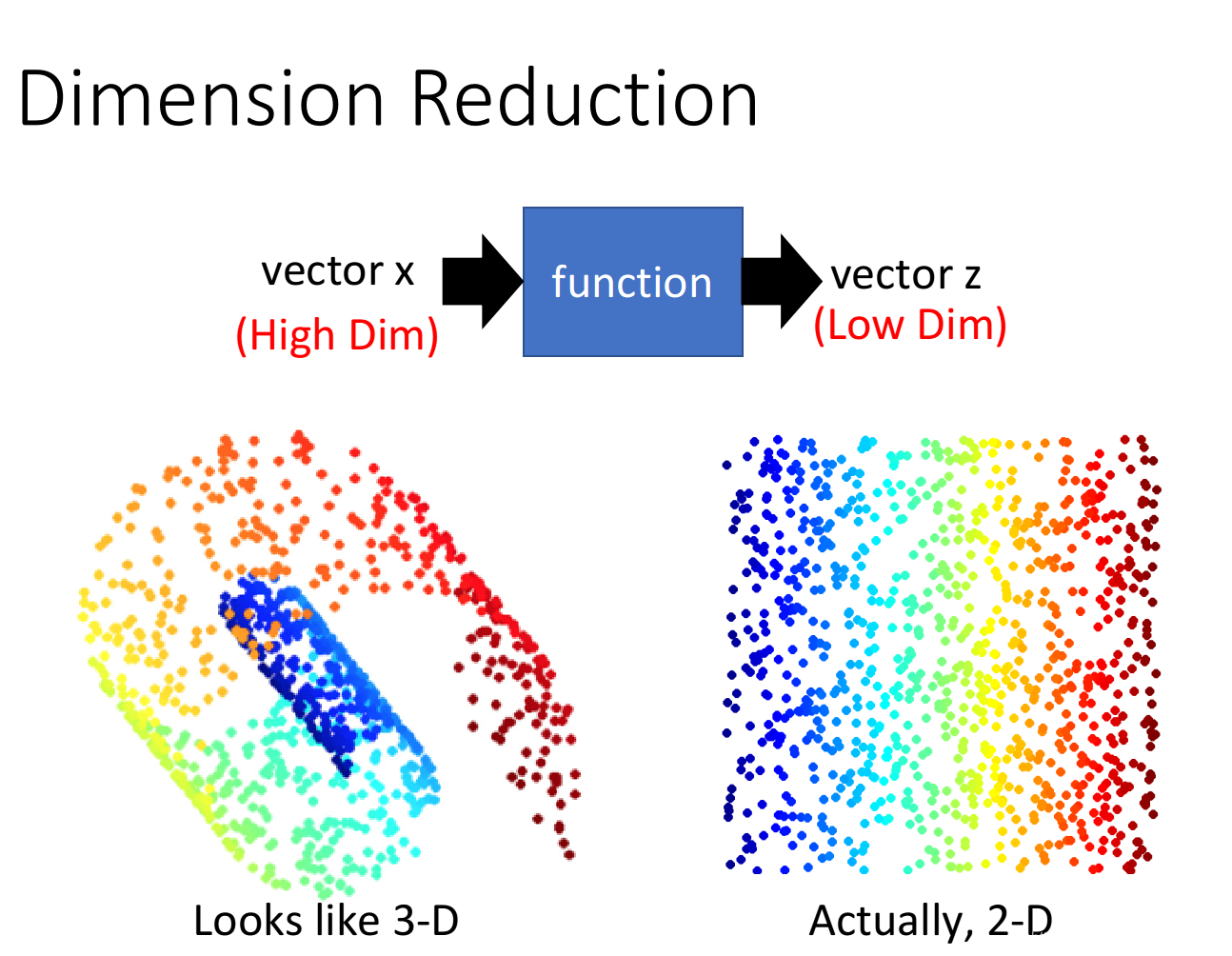
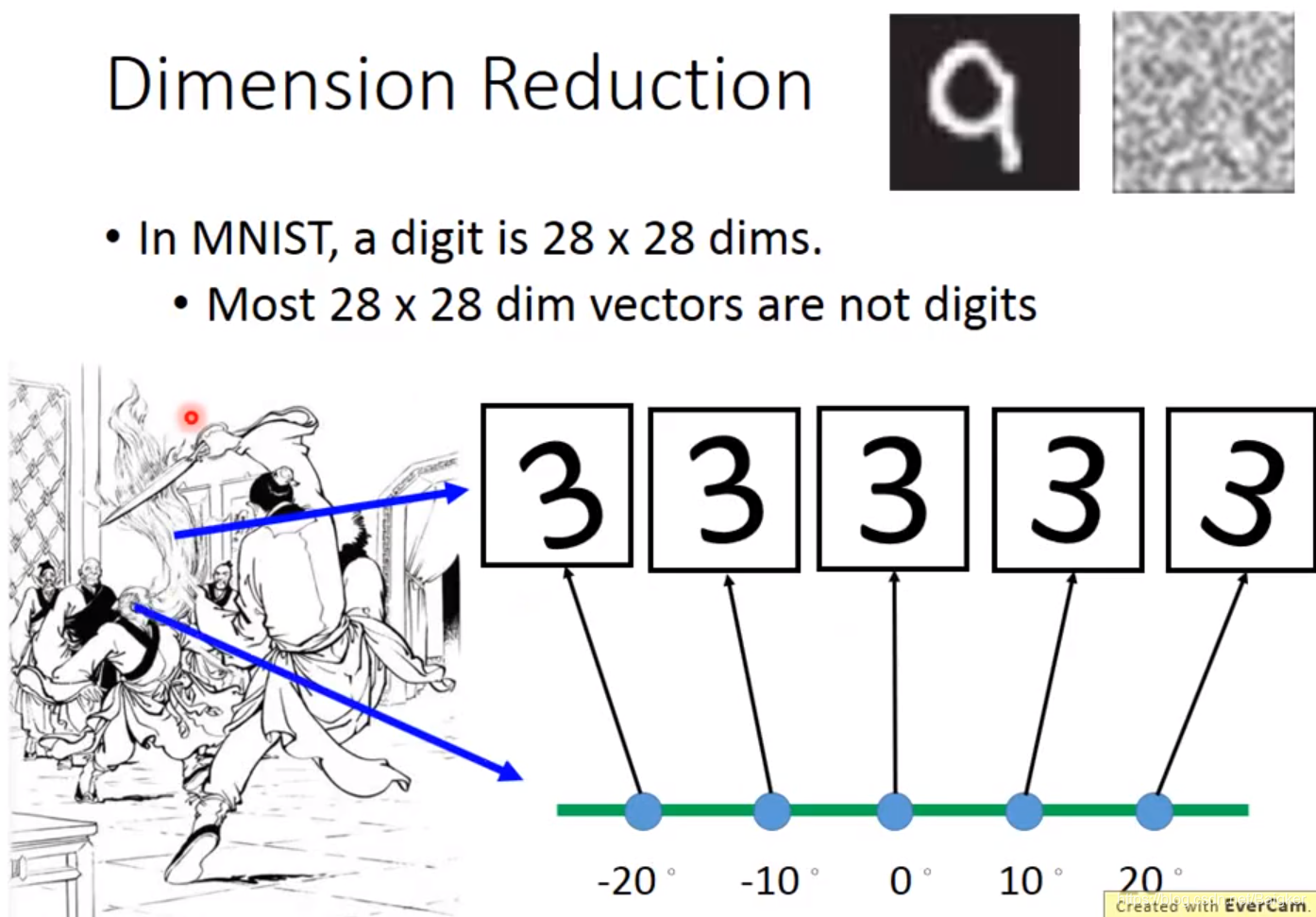
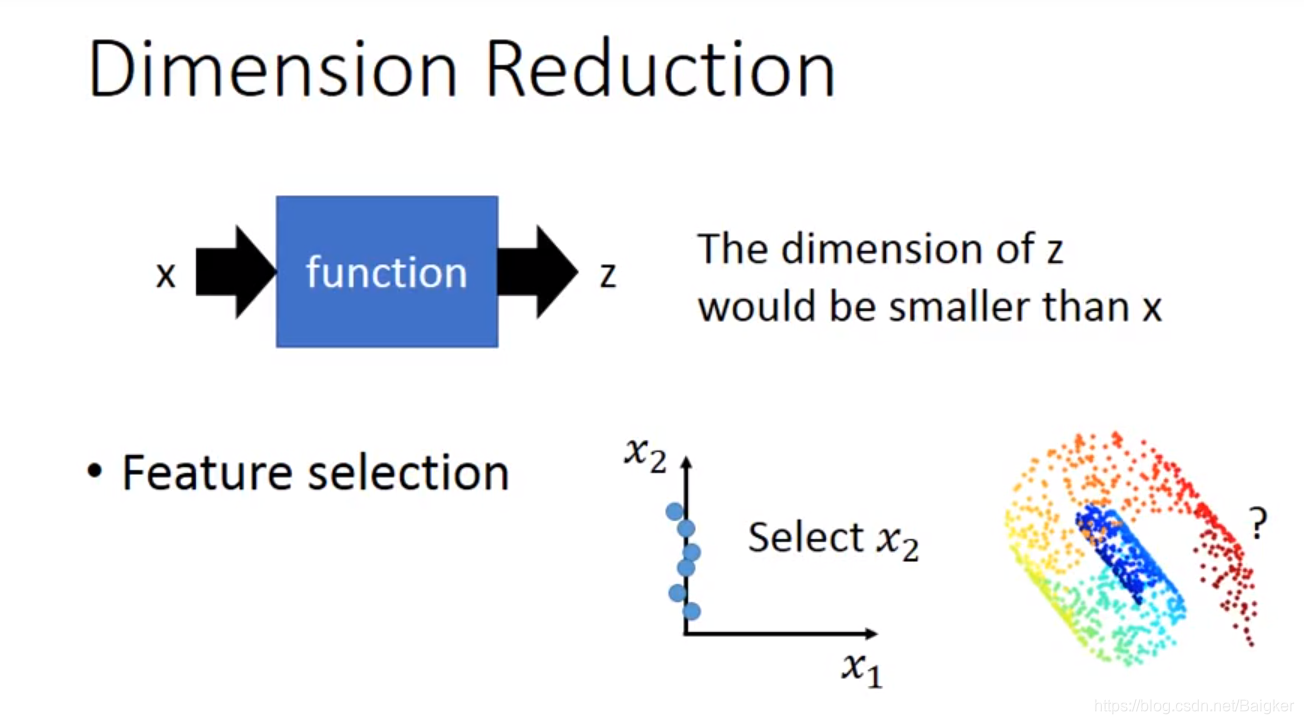
在Dimension Reduction里，我们要找一个function，这个function的input是原始的x，output是经过降维之后的z
最简单的方法是Feature Selection，即直接从原有的dimension里拿掉一些直观上就对结果没有影响的dimension，就做到了降维，比如下图中从$x_1,x_2$两个维度中直接拿掉$x_1$；但这个方法不总是有用，因为很多情况下任何一个dimension其实都不能被拿掉，就像下图中的螺旋卷。

PCA

另一种方法就是PCA。

数学推导

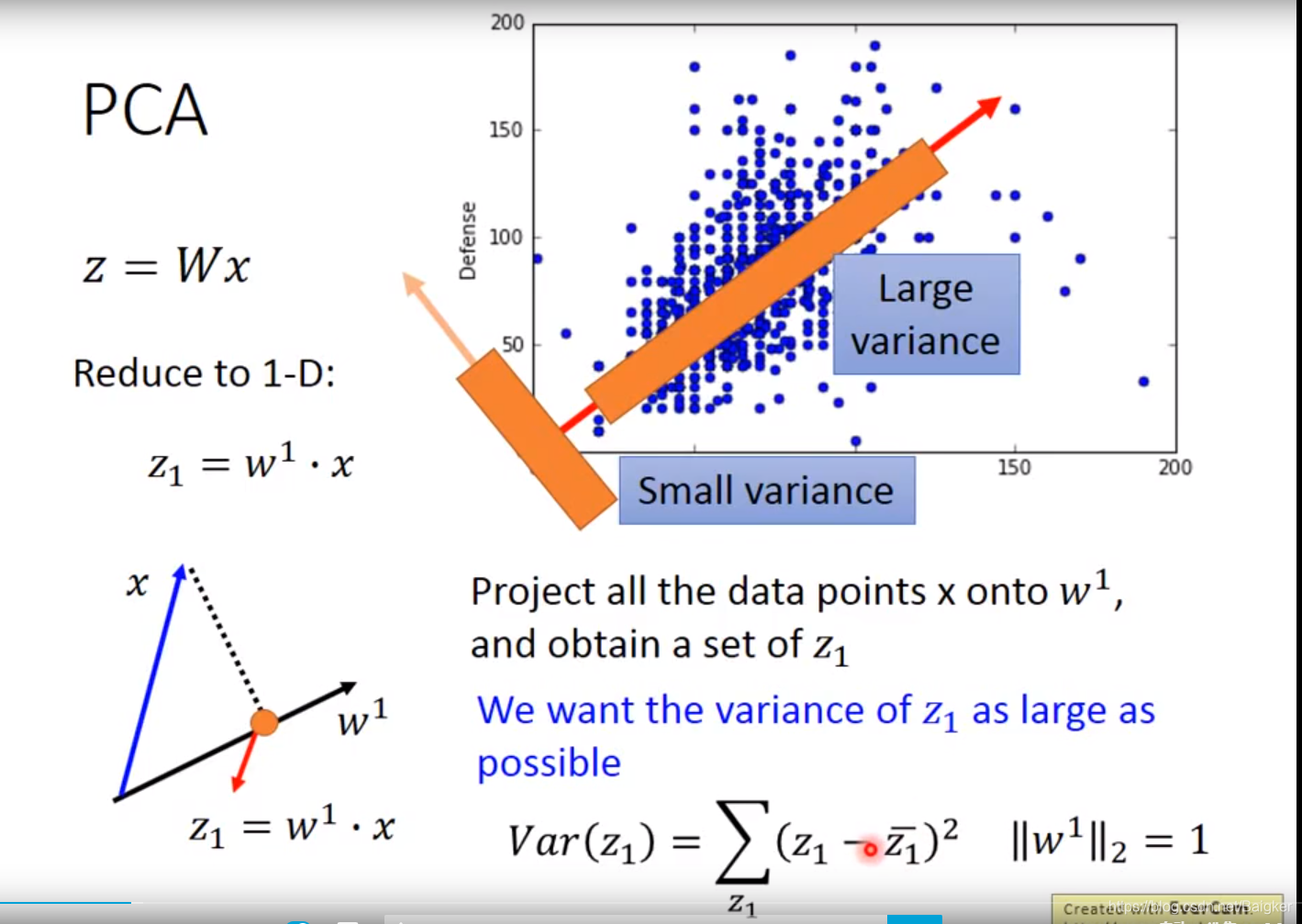
PCA认为，我们只要找到一个$W$，让$z=Wx$降维即可。比如下图中：$x$是宝可梦的攻击力和防御力，我们要找一个$W$，算出宝可梦的战斗力$z$。并且，这些$z$的分布越分散越好（即：$variance$要大）。

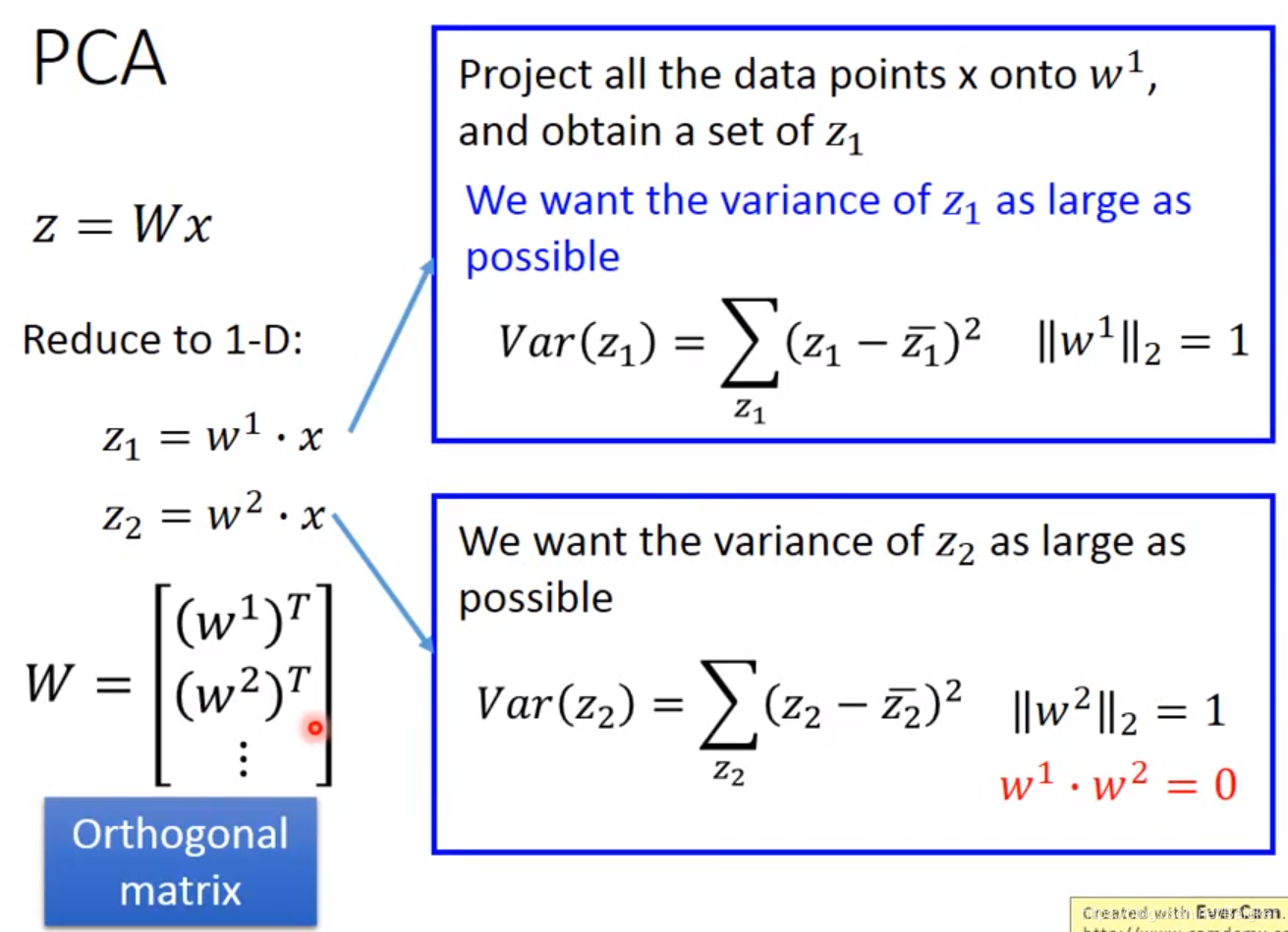
上例是变成1维的情况，变成n维的情况也是一样的。只要求出多个$w$，彼此互相正交，将其拼凑在一起就可以了。

那么，如何求解$w$呢？数学公式如下。

可以看出，数学求导是很长的。但好在可以直接调用函数，其实没那么麻烦。
PCA还有去**相关性（decorrelation）**的作用。
PCA可以让不同dimension之间的covariance变为0，即不同new feature之间是没有correlation的，这样做的好处是，减少feature之间的联系从而减少model所需的参数量。

另一个角度看PCA

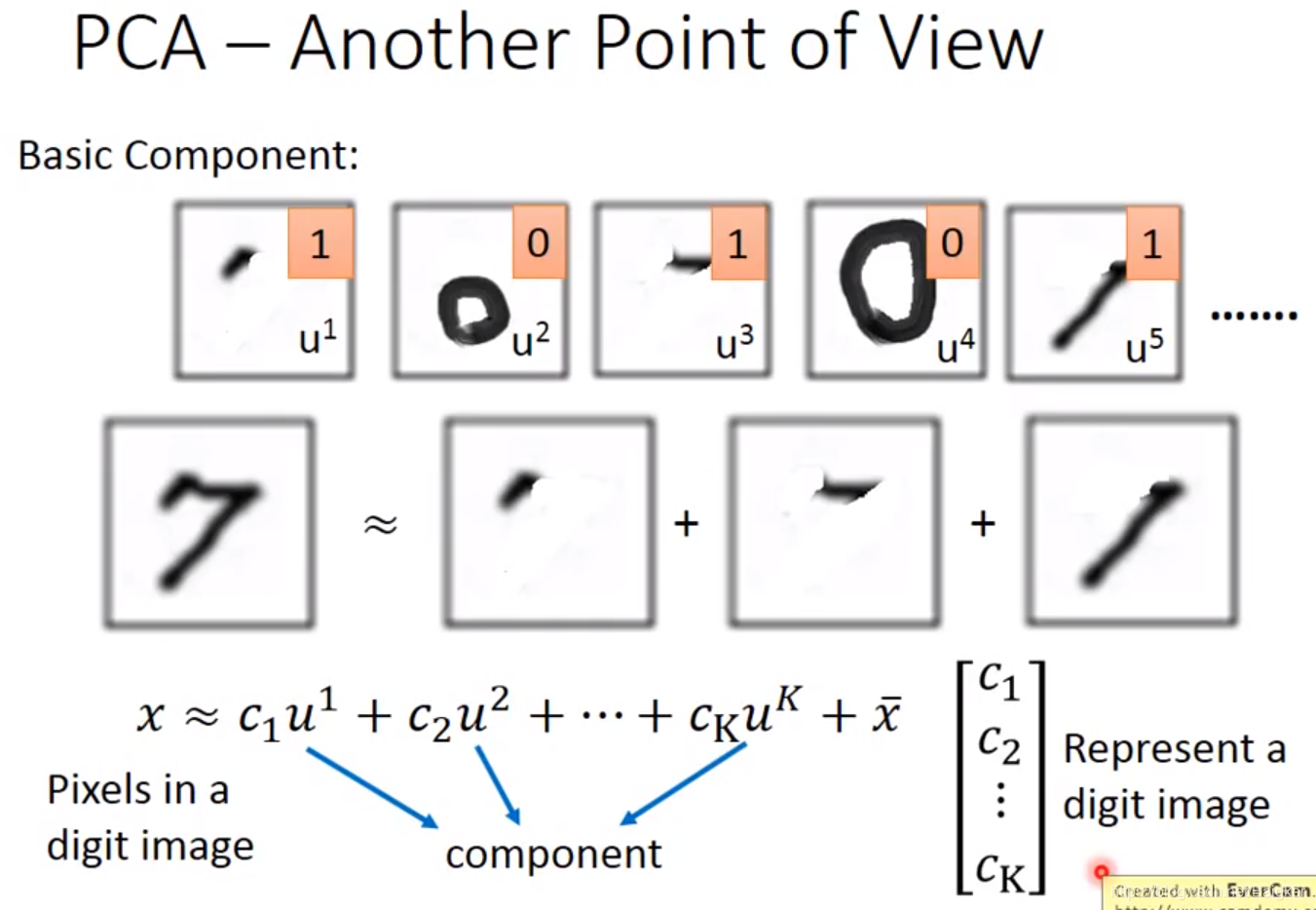
以手写数字识别为例：
我们可以把一个数字看成多个笔画的组合，比如下面的“7”。
对公式的解释：$x$是一张图的所有像素，$c$是权重，$u$表示笔画，$\bar{x}$是所有图片的平均值。

设$\sum c_i{u}^i=\hat{x}$。很显然，我们希望$x?\bar{x}$与KaTeX parse error: Expected 'EOF', got '}' at position 7: \hat x}?越接近越好，即最小化$||(x?\bar{x})?\hat{x}||$。
考虑到我们有多张图片，即多个$x$，就可以写出如下的Loss function。那么目标就是求出$u^1,u^2,...,u^K$。
有趣的是，$u^1,u^2,...,u^K$就是之前PCA求出的$w^1,w^2,...,w^K$。



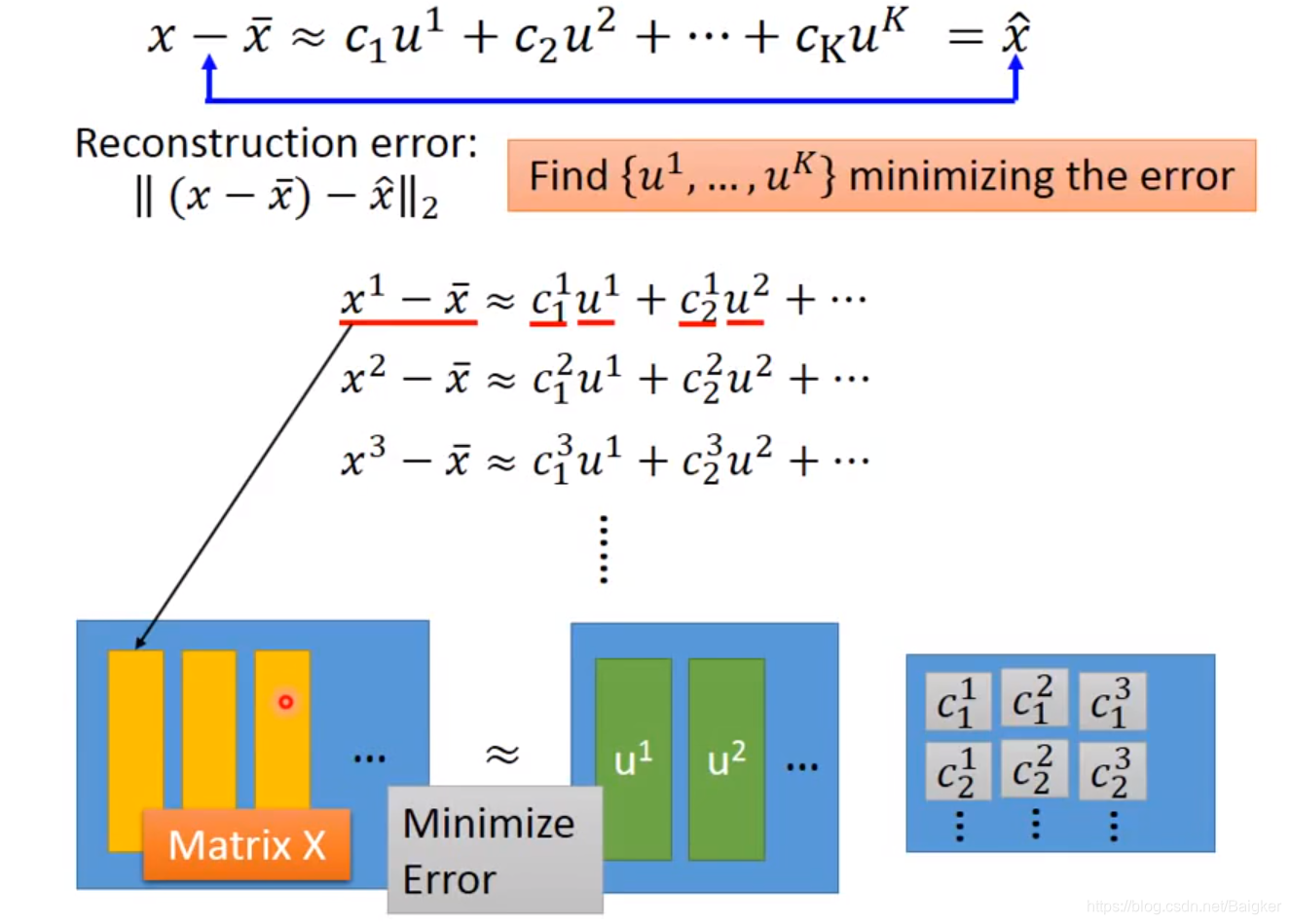
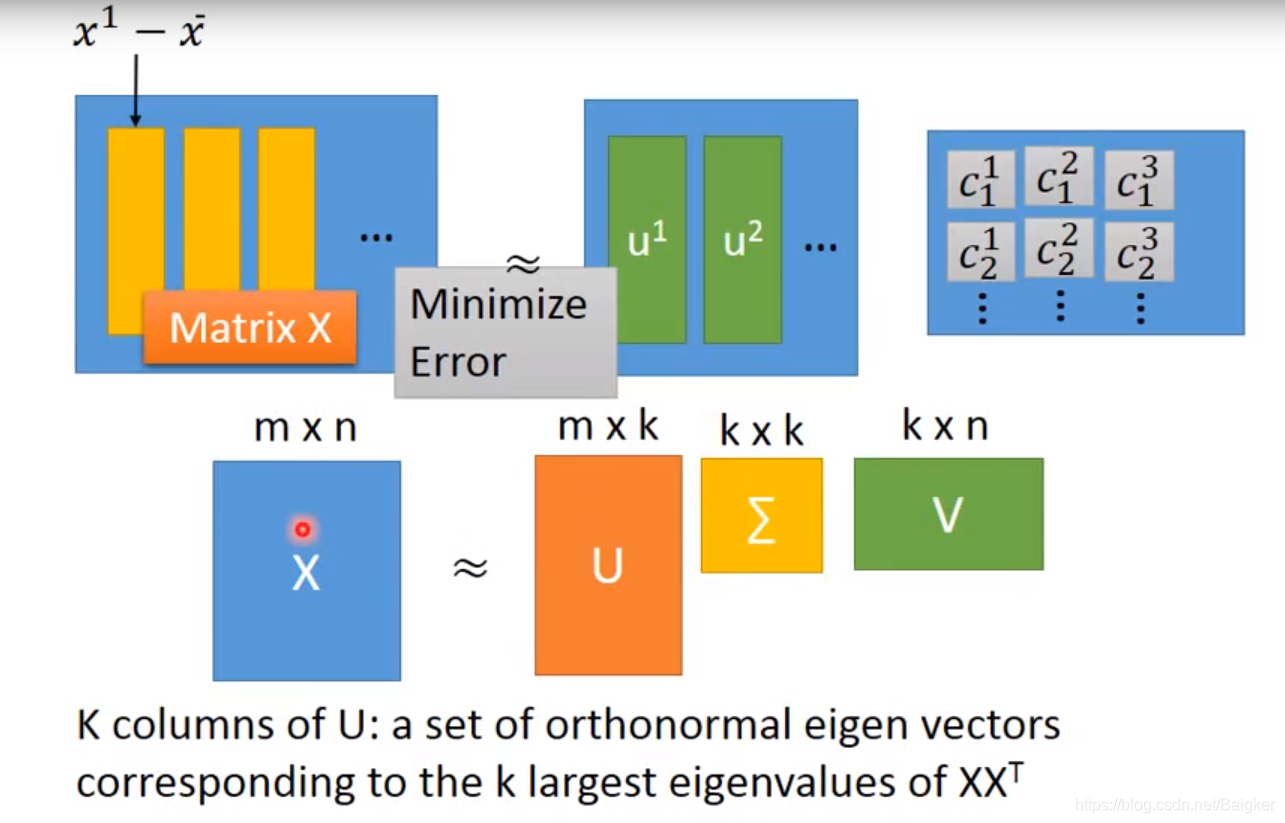
求出矩阵$W$之后，就可以求权值$C$了。

PCA的缺点

1. 它是Unsupervised的。PCA很可能找了一个方向，导致两个class的点被混在了一起。解决方法：使用引入labeled data的LDA方法，但这是supervised的。
2. 它是Linear的。PCA只能把分布打扁，但不能拉直。遇到螺旋形分布时效果很不好。解决方法：使用non-linear transformation。

PCA的例子

宝可梦

每个宝可梦有六个维度即vector={HP, Atk, Def, Sp Atk, Sp Def, Speed}，我们当然可以用PCA来分析宝可梦。
这里有一个技巧：我们可以先找出6个特征向量和对应的特征值${\lambda }_i$，其中${\lambda }_i$表示第i个投影维度的variance有多大(即在第i个维度的投影上点的集中程度有多大)，然后我们就可以计算出每个${\lambda }_i$的比例。比例比较小代表这是所有宝可梦的共性，对我们的分析帮助不大，可以舍弃。比如下图中的5和6。

手写数字识别

可以看出，每个component有的像笔画，比较简单；有的像数字；还有的像玛雅文字，很复杂。
这似乎与我们的初衷（把数字拆分成笔画）有些不符。

人脸识别

到了人脸识别，这个问题更严重了：几乎所有component都是一张脸而非五官！

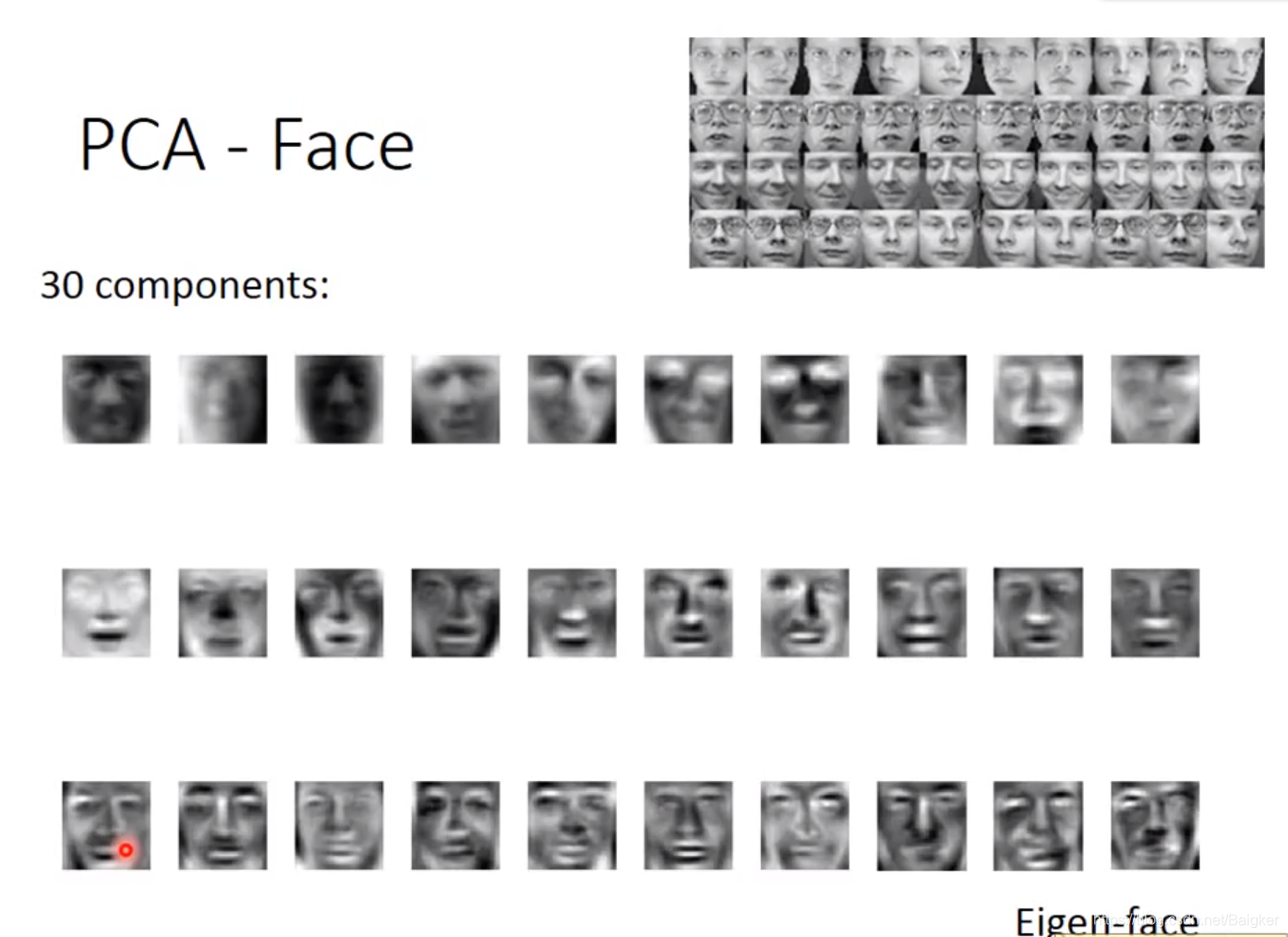
回到公式本身，不难发现原因：$a$可以为负数。这就代表着PCA不一定是让各个component叠加成$x$，还有可能是让它们通过加加减减肯定可以获得基础的组件元素。
这显然不是我们的初衷。

解决方法：NMF。
NMF的基本精神是，强迫使所有组件和它的加权值都必须是正的，也就是说所有图像都必须由组件叠加得到。
这种简单粗暴的方法效果是很好的：

Matrix Factorization

以例子入手：
现在有ABCDE五人的抱枕拥有情况（表格）：

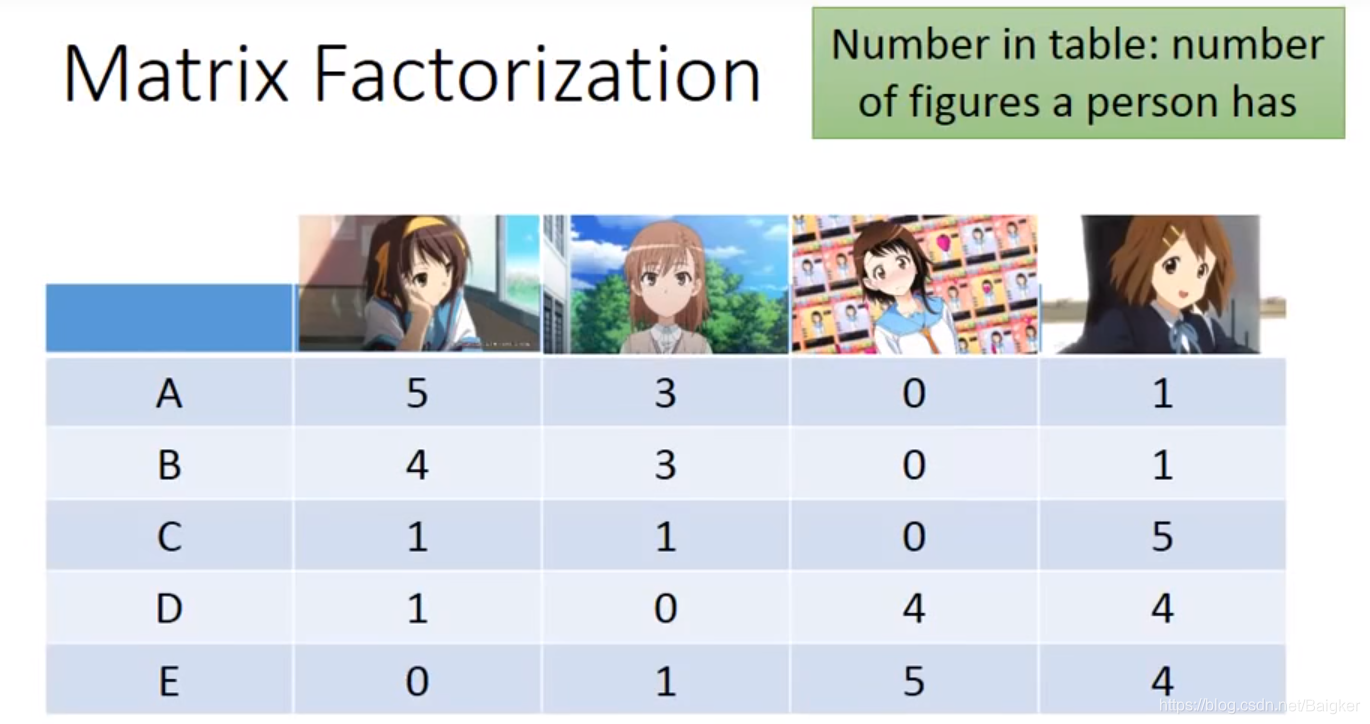
俗话说：没有无缘无故的爱，也没有无缘无故的恨。一个人买什么抱枕必然是有其内在原因，而我们需要探索出其中的原因。
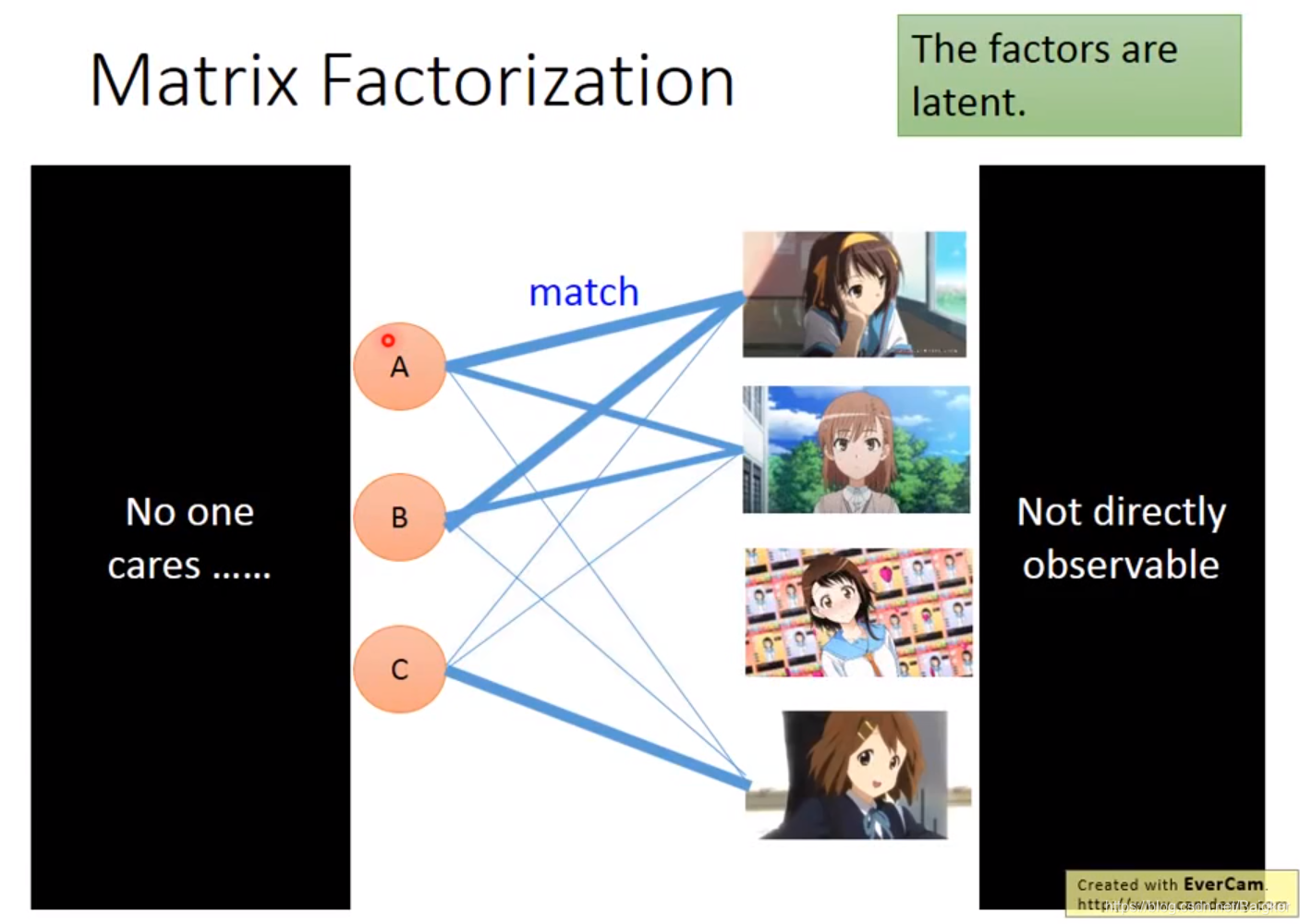
根据之前Reduction的想法，我们有一下猜测：
每个角色有一些属性，其程度可以用一个向量来表示（比如傲娇、天然呆）；每个人对这些属性有不同的喜好，喜好程度也可以用一个向量来表示。
当一个人和一个抱枕相遇时，两个向量的点积就是表格相应的数字。
但问题是，这些向量我们都不知道。这个可以用SVD来解决。

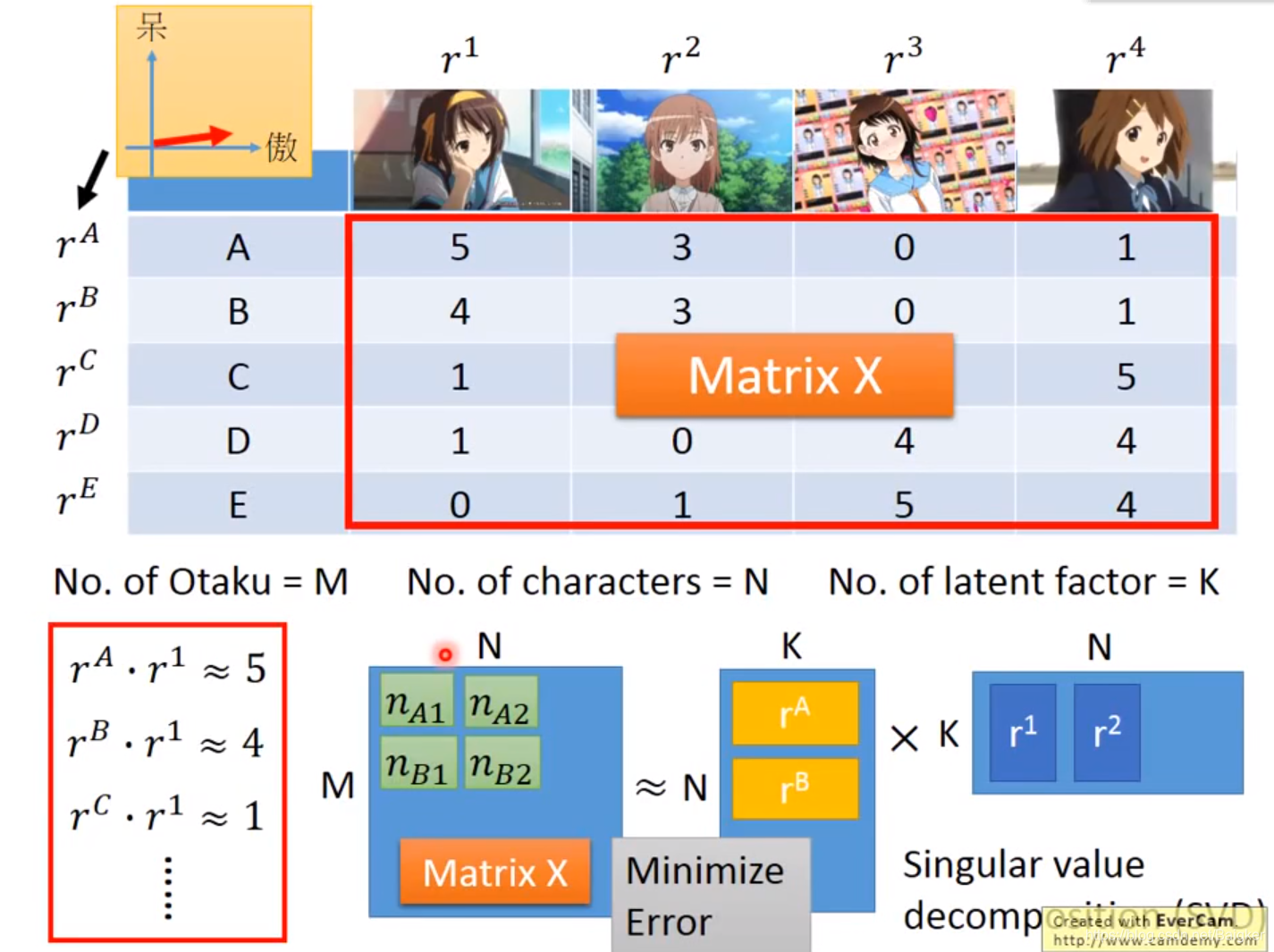
但有时候，表格中有些数据时缺失的。这样就不能用SVD了。
这个时候就要调整使用Gradient Descent来解决。
写出Loss Function：$L=\sum _{(i,j)}(r^i?r^j?n_{ij}{)}^2$后就可以直接Train了。

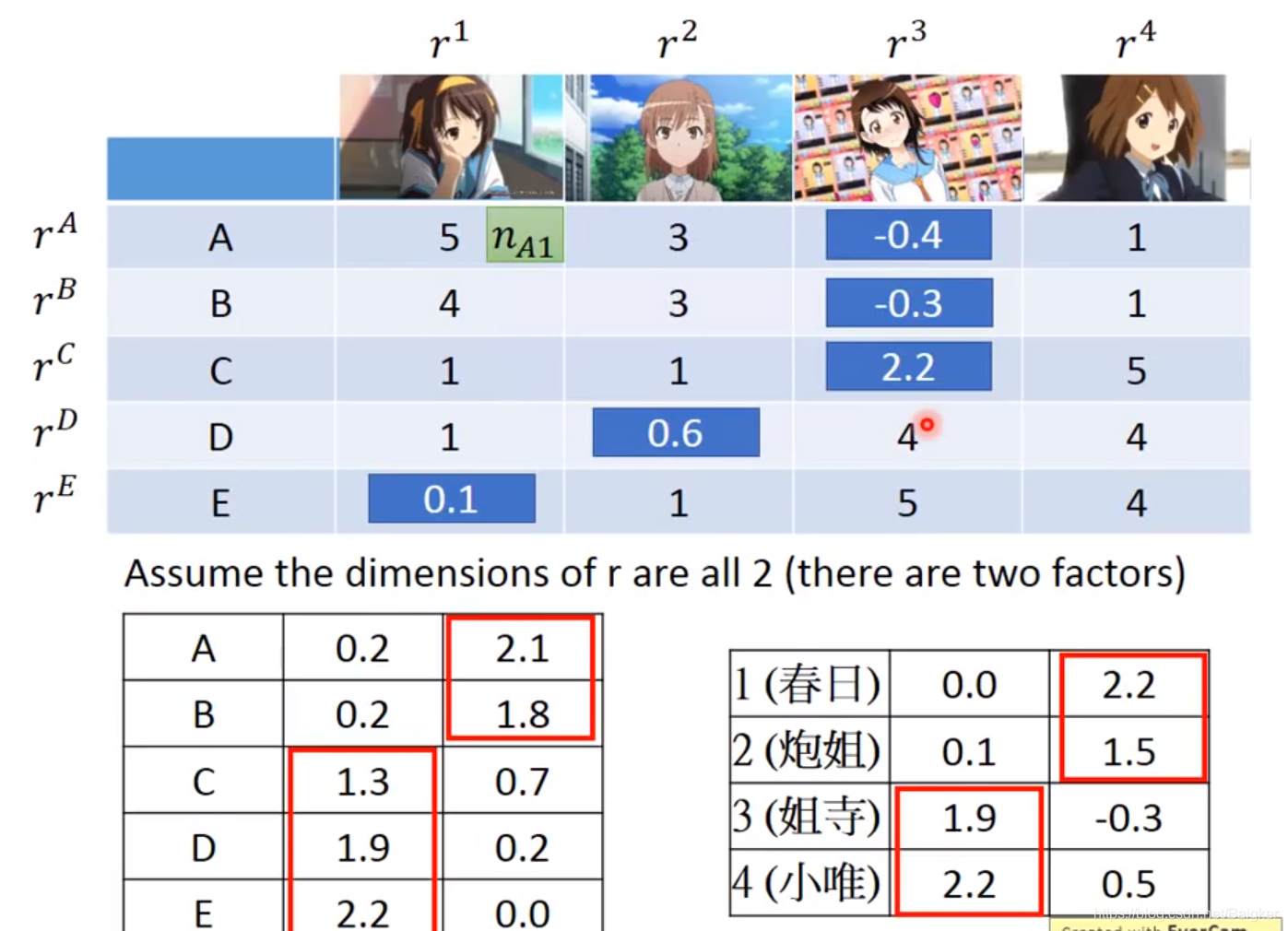
可以看出，结果喜人：每个角色的属性和每个人的喜好都知道了！
因此，这也是推荐系统的常用方法。

实际上除了人和动漫角色的属性之外，可能还存在其他因素操控购买数量这一数值，因此我们可以将式子更精确地改写为： $$r^A?r^1+b_A+b_1\approx 5$$ 其中$b_A$表示A这个人本身有多喜欢买公仔，$b_1$则表示这个动漫角色本身有多让人想要购买，这些内容是跟属性vector无关的，此时loss function被改写为： $$L=\sum _{(i,j)}(r^i?r^j+b_i+b_j?n_{ij}{)}^2$$ 当然你也可以加上一些regularization去对结果做约束。