深度学习(14)TensorFlow高阶操作三: 张量排序
Outline
- Sort/argsort(排序/在序列中的位置)
- Topk(前k个排序结果)
- Top-5 Acc.(Topk应用)
一. Sort, argsort
1. 一维Tensor
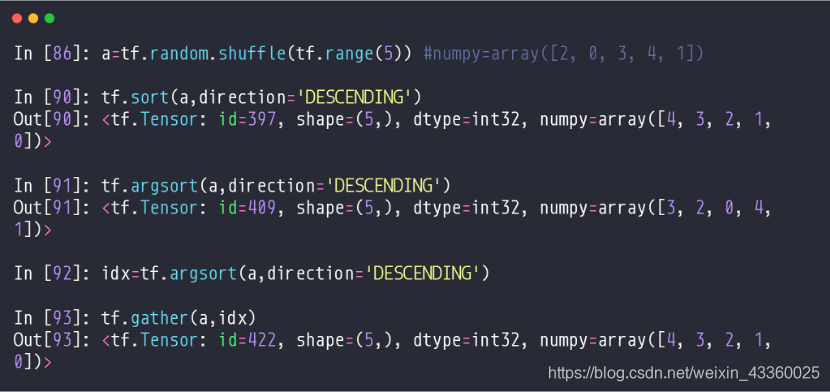
(1) a = tf.random.shuffle(tf.range(5)): 创建一个[0~5]的Tensor,再将其随机打乱,打乱后a=[2, 0, 3, 4, 1];
(2) tf.sort(a, direction=‘DESCENDING’): 将a按降序排列,即按照由大到小进行排列,排列完为[4, 3, 2, 1, 0];
注: 升序就是ASCENDING
(3) tf.argsort(a, direction=‘DESCENDING’): 将a按照降序排列,然后得到每个元素在原来a中的位置。例如,4在原来a中的位置是3,那么argsort中的第1个元素就是3; 3在原来a中的位置是2,那么argsort中的第2个元素就是2; 2在原来a中的位置是0,那么argsort中的第3个元素就是0; 1在原来a中的位置是4,那么argsort中的第4个元素就是4; 0在原来a中的位置是1,那么argsort中的第5个元素就是1; 所以得到argsort=[3, 2, 0, 4, 1];
(4) tf.gather(a, idx): 将a按照idx中的索引来排序,得到[4, 3, 2, 1, 0];
2. 多维Tensor
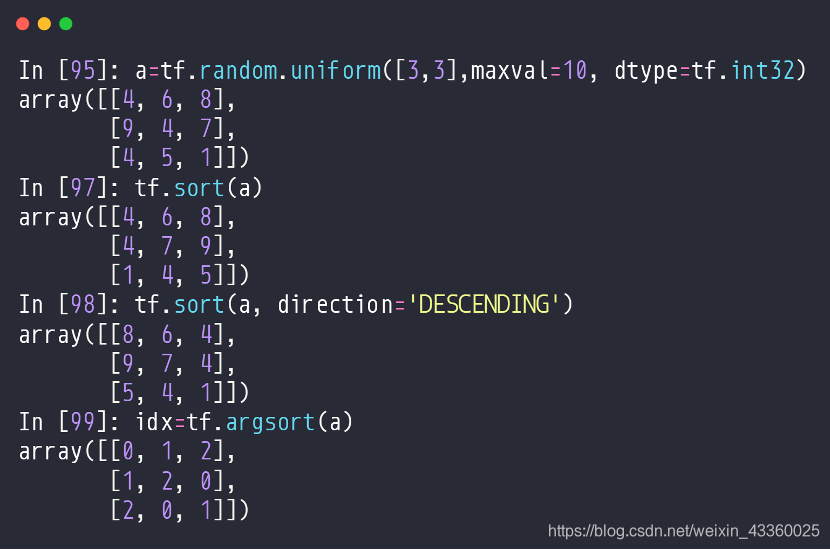
(1) tf.sort(a): 将a升序排列。不指定direction就是默认升序排列;
(2) tf.dort(a, direction=‘DESCENDING’): 将a降序排列;
(3) idx = tf.argsort(a): 将a的升序排列进行索引排列;
二. Top_k
- Only return top-k values and indices
这个方法只能返回tok-k的值和索引。
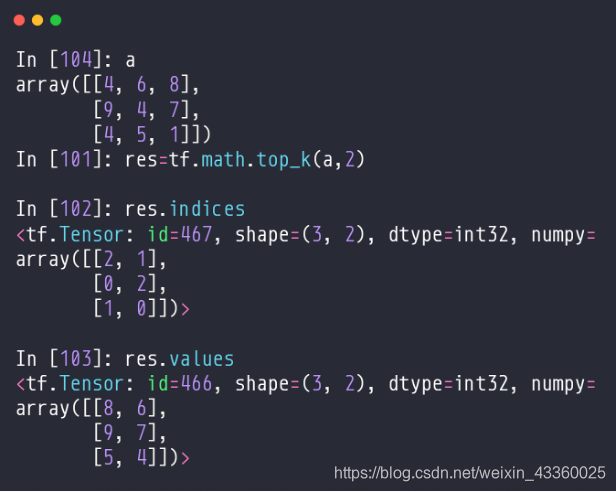
(1) res = tf.math.top_k(a, 2): 将a中每行按照top2排列;
(2) res.indices: 返回res的索引顺序;
(3) rea.values: 返回res的值的顺序;
三. Top-k accuracy(Top-k应用)
1. 问题描述
- Prob: [0.1, 0.2, 0.3, 0.4]
表示数字识别中一个数字为“0”的概率为0.1,为“1”的概率为0.2,为“2”的概率为0.3,为“3”的概率为0.4; - Label:[2]
表示这个数字的标签值(label)为2; - Only consider top-1 prediction: [3]
如果我们只考虑1个最有可能的预测值,就是这个数字为“3”,那么显然与标签值“2”对不上号,那么就会导致正确率为0%; - Only consider top-2 prediction: [3, 2]
如果我们考虑2个最有可能的预测值,使用top-2排列为[3, 2],这时准确率就为100%(只要top-2中出现预测值与标签值相同的情况,准确率就记为1); - Only consider top-3 prediction: [3, 2, 1]
如果我们考虑3个最有可能的预测值,使用top-3排列为[3, 2, 1],这时准确率就为100%;
2. 问题解决
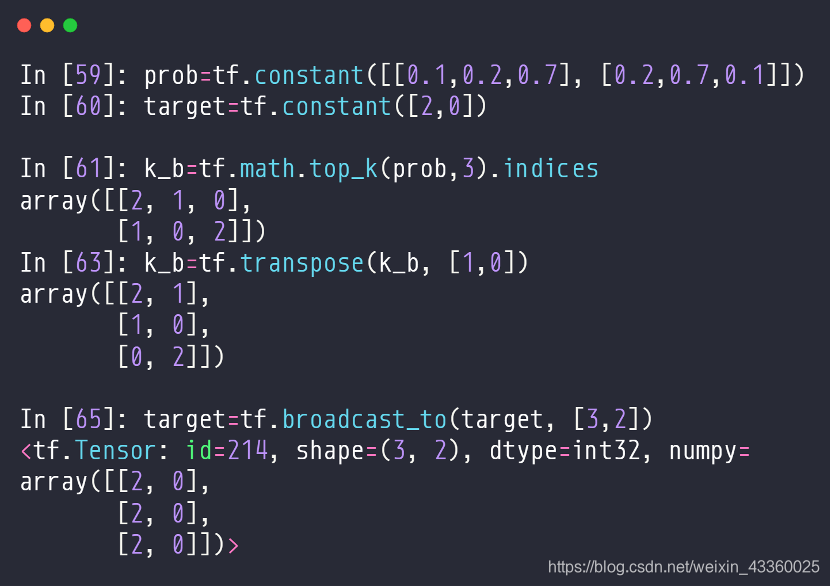
(1) target = tf.constant([2, 0]): 表示标签(label)值,即第1个样本的真实值为“2”, 第2个样本的真实值为“0”;
(2) k_b = tf.math.top_k(prob, 3).indices: 表示将prob中的数据按照top-3排列并给出索引,这个结果也相当于这两个样本每个样本是什么数字的可能性,即第1个样本最有可能是“2”,次有可能是“1”,再次有可能是“0”; 第2个样本最有可能是“1”,次有可能是“0”,再次有可能是“2”;
(3) k_b = tf.transpose(k_b, [1, 0]): 将k_b做转置操作,即将维度由[0, 1]变为[1, 0],这样的话,第1行就对应这两个样本最有可能(即top1)的预测值,第2行就对应这两个样本次有可能(即top2)的预测值;
(4) target = tf.broadcast_to(target, [3, 2]): 使用Broadcasting方法将target的维度由[2]扩展为[3, 2]([2]
→
\to
→ [1, 2]
→
\to
→ [3, 2]);

接下来我们需要将预测值与标签值进行比较操作,例如: 使用top1的预测值比较,即使用[2, 1]和[2, 0]进行比较,结果为[True, False],那么其准确率就为50%,因为只有1个数字识别正确; 使用top2的预测值比较,即使用[[2, 1], [1, 0]]和[[2, 0], [2, 0]]进行比较,那么我们只需要保证top2的每个数字的预测值有1个与标签值相等即可,结果为[True, True],那么其准确率就为100%; 使用top3的预测值比较,即使用[[2, 1], [1, 0], [0, 2]]和[[2, 0], [2, 0], [2, 0]]进行比较,那么我们只需要保证top3的每个数字的预测值有1个与标签值相等即可,结果为[True, True, True],那么其准确率还是100%;
(5) def accuracy(output, target, topk=(1,)): 定义accuracy方法,其中output.shape=[2, 3],即共有2个样本,每个样本有3种分类; target.shape=[2],即target为这2个样本的标签值(label); topk=(1,)表示取值top1;
(6) maxk = max(topk): 表示取最大的top值,例如topk=(1,),那么maxk就取1,也就意味着在后边的操作中我们使用top1计算accuracy; topk=(1, 2),那么maxk就取2,也就意味着在后边的操作中我们使用top2计算accuracy; topk=(1, 2, 3),那么maxk就取3,也就意味着在后边的操作中我们使用top3计算accuracy;
(7) batch_size = target.shape[0]: target.shape=[2],所以batch_size=2;
(8) pred = tf.math.topk(output, maxk).indicies: 将每个样本预测值按照topk的索引进行排列,例如,如果按照top1排列,那么tf.math.topk(output, 1).indicies就为:
| 样本 | 预测值 |
|---|---|
| b 0 b_0 b0? | 2 |
| b 1 b_1 b1? | 1 |
也就是:
[
2
1
]
\begin{bmatrix}2\\1\end{bmatrix}
[21?]
如果按照top2排列,那么tf.math.topk(output, 2).indicies就为:
| 样本 | 预测值top1 | 预测值top2 |
|---|---|---|
| b 0 b_0 b0? | 2 | 1 |
| b 1 b_1 b1? | 1 | 0 |
也就是:
[
2
1
1
0
]
\begin{bmatrix}2&1\\1&0\end{bmatrix}
[21?10?]
如果按照top1排列,那么tf.math.topk(output, 3).indicies就为:
| 样本 | 预测值top1 | 预测值top2 | 预测值top3 |
|---|---|---|---|
| b 0 b_0 b0? | 2 | 1 | 0 |
| b 1 b_1 b1? | 1 | 0 | 2 |
也就是:
[
2
1
0
1
0
2
]
\begin{bmatrix}2&1&0\\1&0&2\end{bmatrix}
[21?10?02?]
(9) pred = tf.transpose(pred, perm=[1, 0]): 将pred进行转置操作,也就是将pred的维度顺序索引由[0, 1]变为[1, 0],即:
如果按照top1排列,那么pred就为:
[
2
1
]
\begin{bmatrix}2&1\end{bmatrix}
[2?1?]
如果按照top2排列,那么pred就为:
[
2
1
1
0
]
\begin{bmatrix}2&1\\1&0\end{bmatrix}
[21?10?]
如果按照top3排列,那么pred就为:
[
2
1
1
0
0
2
]
\begin{bmatrix}2&1\\1&0\\0&2\end{bmatrix}
???210?102????
(10) target_ = tf.broadcast_to(target, pred.shape)
将target进行Broadcasting操作,使target.shape=pred.shape,即:
如果按照top1排列,那么target_就为:
[
2
0
]
→
[
2
0
]
\begin{bmatrix}2&0\end{bmatrix}\to\begin{bmatrix}2&0\end{bmatrix}
[2?0?]→[2?0?]
如果按照top2排列,那么target_就为:
[
2
0
]
→
[
2
0
2
0
]
\begin{bmatrix}2&0\end{bmatrix}\to\begin{bmatrix}2&0\\2&0\end{bmatrix}
[2?0?]→[22?00?]
如果按照top3排列,那么target_就为:
[
2
0
]
→
[
2
0
2
0
2
0
]
\begin{bmatrix}2&0\end{bmatrix}\to\begin{bmatrix}2&0\\2&0\\2&0\end{bmatrix}
[2?0?]→???222?000????
(11) correct = tf.equal(pred, target_): 将pred与target_做比较操作,即:
如果按照top1排列,那么correct就为:
[
T
r
u
e
F
a
l
s
e
]
\begin{bmatrix}True&False\end{bmatrix}
[True?False?]
如果按照top2排列,那么pred就为:
[
T
r
u
e
F
a
l
s
e
F
a
l
s
e
T
r
u
e
]
\begin{bmatrix}True&False\\False&True\end{bmatrix}
[TrueFalse?FalseTrue?]
如果按照top3排列,那么pred就为:
[
T
r
u
e
F
a
l
s
e
F
a
l
s
e
T
r
u
e
F
a
l
s
e
F
a
l
s
e
]
\begin{bmatrix}True&False\\False&True\\False&False\end{bmatrix}
???TrueFalseFalse?FalseTrueFalse????
(12) res[]: 新建res列表,用于存放准确率结果;
(13) correct_k = tf.cast(tf.reshape(correct[:k], [-1]), dtype=tf.float32):
其中correct[:k]表示correct的前k-1行;
tf.reshape(correct[:k], [-1])表示将correct的前k-1行进行reshape操作,即: 如果按照top1排列,那么correct[:k].shape就由[1, 2]变为[1]; 如果按照top2排列,那么correct[:k].shape就由[2, 2]变为[2]; 如果按照top3排列,那么correct[:k].shape就由[3, 2]变为[3];
tf.cast(tf.reshape(correct[:k], [-1]), dtype=tf.float32)表示将reshape后的correct里的数据类型变为tf.float32,即将True变为1,False变为0;
(14) correct_k = tf.reduce_sum(correct_k): 将correct_k中的每行数据求和,即:
如果按照top1排列,那么
c
o
r
r
e
c
t
_
k
=
1
+
0
=
1
correct\_k=1+0=1
correct_k=1+0=1;
如果按照top2排列,那么
c
o
r
r
e
c
t
_
k
=
1
+
0
+
0
+
1
=
2
correct\_k=1+0+0+1=2
correct_k=1+0+0+1=2;
如果按照top3排列,那么
c
o
r
r
e
c
t
_
k
=
1
+
0
+
0
+
1
+
0
+
0
=
2
correct\_k=1+0+0+1+0+0=2
correct_k=1+0+0+1+0+0=2;
(15) acc = float(correct_k / batch_size): 计算top_k的准确率;
(16) res.append(acc): 将准确率acc放入到结果res中;
3. 代码
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
tf.random.set_seed(2467)
def accuracy(output, target, topk=(1,)):
maxk = max(topk)
batch_size = target.shape[0]
pred = tf.math.top_k(output, maxk).indices
pred = tf.transpose(pred, perm=[1, 0])
target_ = tf.broadcast_to(target, pred.shape)
# [10, b]
correct = tf.equal(pred, target_)
res = []
for k in topk:
correct_k = tf.cast(tf.reshape(correct[:k], [-1]), dtype=tf.float32)
correct_k = tf.reduce_sum(correct_k)
acc = float(correct_k* (100.0 / batch_size) )
res.append(acc)
return res
output = tf.random.normal([10, 6])
output = tf.math.softmax(output, axis=1)
target = tf.random.uniform([10], maxval=6, dtype=tf.int32)
print('prob:', output.numpy())
pred = tf.argmax(output, axis=1)
print('pred:', pred.numpy())
print('label:', target.numpy())
acc = accuracy(output, target, topk=(1,2,3,4,5,6))
print('top-1-6 acc:', acc)
运行结果如下:

可以看到,随着top-k的增加,准确率不断提升,在数字识别种类有6种(即0~5)的情况下,如果我们计算top-6的话,准确率是一定会达到100%的。
参考文献:
[1] 龙良曲:《深度学习与TensorFlow2入门实战》
